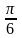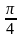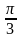- •Учетно-финансовый факультет кафедра статистики и прикладной математики
- •Содержание
- •1 Случайные события
- •2 Основные теоремы и их следствия
- •3 Повторные независимые испытания
- •4 Дискретные случайные величины
- •5 Непрерывные случайные величины
- •6 Законы распределения случайных величин
- •Определить: а) интегральную функцию случайной величины х; б) вероятность попадания случайной величины в интервал (- ).
- •7 Функции случайных величин
- •8 Закон больших чисел
- •Многомерные случайные величины
- •11 Вариационные ряды
- •12 Выборочный метод
- •Распределение семей по величине месячного дохода
- •Результаты откорма свиней в опыте
- •13 Проверка статистических гипотез
- •14 Дисперсионный анализ
- •15 Корреляционно-регрессионный анализ
- •16 Анализ временных рядов
- •Ответы раздел 1
- •Раздел 2
- •Аздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 6
- •Раздел 7
- •Раздел 8
- •Раздел 9
- •Раздел 10.
- •Раздел 11.
- •Раздел 12.
Определить: а) интегральную функцию случайной величины х; б) вероятность попадания случайной величины в интервал (- ).
Случайная величина Х распределена по закону Релея
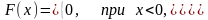
Найти: а) дифференциальную функцию случайной величины Х; б) вероятность попадания случайной величины в интервал (1; 2), при а = 1; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
Функция распределения годовых доходов лиц, облагаемых налогом, имеет вид:
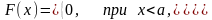
Определить:
а) размер годового дохода, который для
случайно взятого лица будет превышен
с вероятностью 0,8; б)дифференциальную
функцию случайной величины Х;
в)математическое ожидание случайной
величины Х при
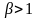 .
.
7 Функции случайных величин
а) Функция одного случайного аргумента.
Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины У, то У называют функцией случайного аргумента Х. У = φ(Х).
Пусть аргумент Х дискретная случайная величина. Тогда случайная величина У = φ(Х) также дискретная случайная величина.
Если
аргумент Х принимает значение хi
с вероятностью Рxi,
то случайная величина У принимает
значение
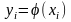 с той же вероятностью
с той же вероятностью
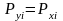 .
.
Пусть аргумент Х – непрерывная случайная величина, заданная плотностью распределения f(x). Если у = φ(х) – дифференцируемая, строго возрастающая или строго убывающая функция, обратная функция которой х = ψ(y), то плотность распределения g(у) случайной величины У находится:
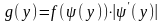 .
(7.1)
.
(7.1)
Если функция У = φ(Х) в интервале возможных значений Х не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция φ(х) монотонна, и найти плотности распределения gi(у) для каждого из интервалов монотонности, а затем предоставить g(у) в виде суммы:
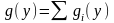 .
(7/2)
.
(7/2)
Например,
если функция φ(х) монотонна на двух
интервалах, в которых соответствующие
обратные функции
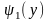 и
и
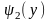 то
то
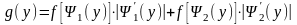 .
(7.3)
.
(7.3)
б) Функция двух случайных аргументов.
Если каждой паре возможных значений случайна величин Х и У соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов Х и У.
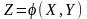 .
(7/4)
.
(7/4)
Если
Х и У – дискретные независимые случайные
величины, то для того чтобы, найти
распределение функции Z
= X + Y надо
найти все возможные значения
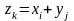 и
их вероятности
и
их вероятности
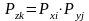 .
.
Если Х и У – непрерывные случайные величины , то плотность распределения g(z) суммы Z = X + Y, при условии, что плотность распределения хотя бы одного из аргументов задана в интервале (- ∞; ∞), находится по формуле:
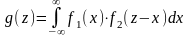 ,
или
,
или
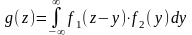 , (7/5)
, (7/5)
где f1 и f2 – плотности распределения аргументов Х и У.
Если возможные значения аргументов неотрицательны, то плотность распределения g(z) величины Z = X + Y находят по формуле:
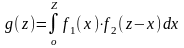 ,
или
,
или
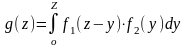 .
(7.6)
.
(7.6)
Если
Х и У – независимые случайные величины,
заданные соответствующими плотностями
распределения
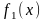 и
и
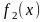 ,
то вероятность попадания случайной
точки (Х, У) в область S
равна:
,
то вероятность попадания случайной
точки (Х, У) в область S
равна:
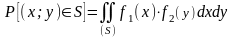 .
(7.7)
.
(7.7)
Дискретная случайная величина задана законом распределения:
Х |
0 |
1 |
4 |
р |
0,3 |
0,5 |
0,2 |
Найти закон распределения случайной величины У, где: а) У=2Х-1;
б)
У=Х+5; в) У=Х2-2; г) У=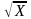 .
Определить М(У).
.
Определить М(У).
Дискретная случайная величина Х задана законом распределения:
Х |
-2 |
-1 |
0 |
1 |
р |
0,2 |
0,4 |
0,1 |
0,3 |
Найти
закон распределения случайной величины
У, где: а) У=2Х+1; б)У=Х3-1; в) У=Х2;
г) У=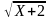 .
Определить М(У).
.
Определить М(У).
Дискретная случайная величина Х задана законом распределения:
Х |
1 |
2 |
4 |
5 |
р |
0,1 |
0,3 |
0,2 |
0,4 |
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины У, если: а) У=4Х-4; б) У=Х2.
Дискретная случайная величина Х задана законом распределения:
Х |
|
|
|
р |
0,2 |
0,7 |
0,1 |
Найти: а) закон распределения случайной величины У=sin2 X; б) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины У.
Случайная величина Х равномерно распределена на интервале (2;10). Найти дифференциальную функцию случайной величины: а) Y = 0,5 X – 1; б) Y = X2; в)
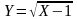 .
Определить М(У), Д(У), σ(У).
.
Определить М(У), Д(У), σ(У).Случайная величина Х равномерно распределена в интервале ( -
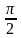 ;
). Найти дифференциальную функцию
случайной величины:
;
). Найти дифференциальную функцию
случайной величины:
а) Y = sin X; б) У= cos X.
Случайная величина Х распределена нормально с параметрами а = 2, =1. Найти дифференциальную функцию случайной величины:
а) У=2Х+6; б) У=Х3.
Непрерывная случайная величина Х задана функцией
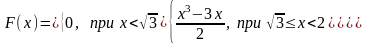
Найти
дифференциальную функцию случайной
величины: а)
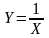 ;
б)
;
б)
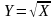 .
.
Сторона квадрата Х имеет равномерное распределение на отрезке [1;2]. Найти плотность вероятности площади квадрата.
Случайная величина Х распределена по закону Коши:
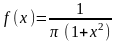 .
.
Найти дифференциальную функцию случайной величины: а) У=Х3;
б) У=3Х.
Независимые случайные величины Х и У распределены равномерно. Случайная величина Х распределена в интервале (0; 2), а случайная величина У в интервале (0; 10). Найти интегральную и дифференциальную функции случайной величины Z=X+У. Построить графики интегральной и дифференциальной функций случайной величины Z.
Случайная величина Х равномерно распределена в интервале (-4; 1), а случайная величина У равномерно распределена в интервале (1; 6). Найти дифференциальную функцию случайной величины Z=X+У и начертить ее график.
Независимые случайные величины Х и У заданы дифференциальными функциями:
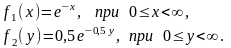
Найти дифференциальную функцию случайной величины Z=X+У.
Независимые случайные величины Х и У распределены по нормальному закону:
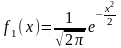 ,
,
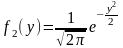 .
.
Найти дифференциальную функцию случайной величины Z=X+У. Показать, что случайная величина Z распределяется по нормальному закону.
Натуральный логарифм некоторой случайной величины Х распределен по нормальному закону с центром рассеивания
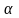 и средним квадратическим отклонением
.
Найти плотность распределения случайной
величины Х.
и средним квадратическим отклонением
.
Найти плотность распределения случайной
величины Х.