Практичне закріплення вивченого

ЗАДАЧА 1

Віднайти швидкість течії про трубі вуглекислого газу, якщо відомо, що за півгодини через поперечний перетин труби протікає m=0,51 кг газу. Густину газу ρ прийняти за 7,5 кг/м³. Діаметр труби дорівнює d = 2 см.

Дано: СІ

t = 30 хв t =1800 с

m=0,51 кг m=0,51 кг

ρ = 7,5 кг/м³ ρ = 7,5 кг/м³

d = 2 см d = м

Знайти: υ - ?

Розв`язання:

Об`єм газу, що протікає за 1 секунду через поперечний перетин труби, дорівнює:

.

За весь час t об’єм газу, що протікатимемо через поперечний перетин труби, дорівнюватиме:

,

де S - площа поперечного перетину труби,

υ – швидкість течії газу про трубі.

Звідси:

Враховуючи, що , , отримаємо формулу для визначення швидкості руху газу по трубі:

.

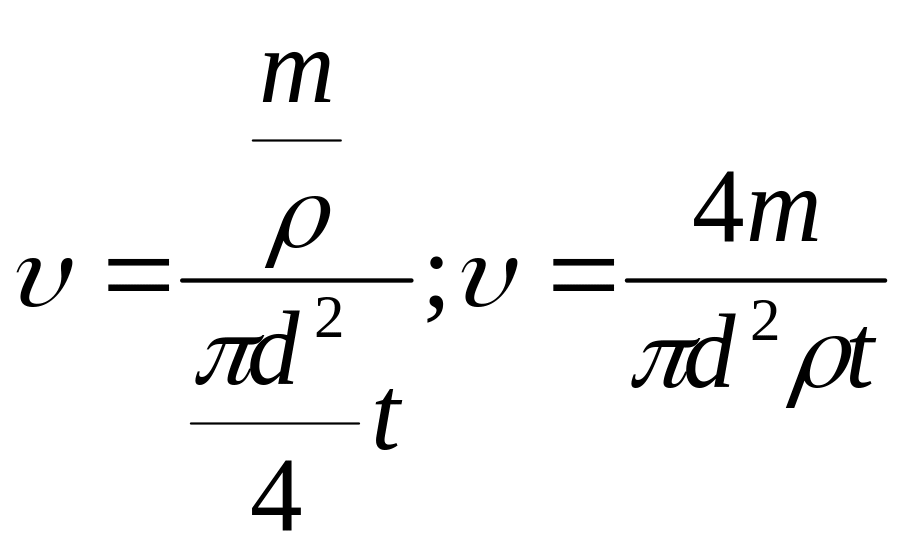Підставляємо чисельні дані:

.

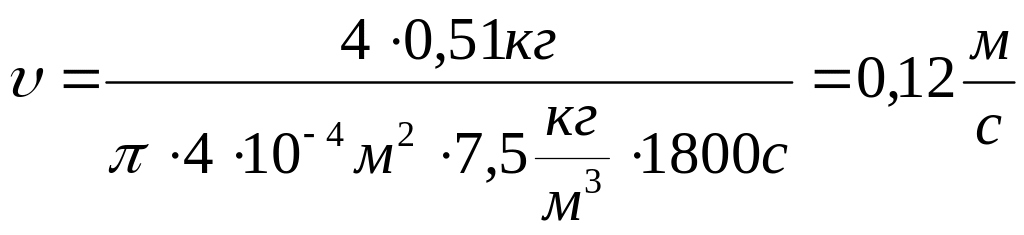Відповідь: υ = 0,12 м/с.

ЗАДАЧА 2

Вода тече по трубі, причому за час t = 1 сек через поперечний перетин труби протікає V = 200 см³ води. Динамічна в’язкість води в умовах досліду дорівнює η = 0,001 Па·с. При якому найбільшому діаметрі труби D рух води залишиться ламінарним? Критичне значення числа Рейнольдса вважати рівним Re_кр = 3000.

Дано: СІ

t = 1 с t = 1 с

V = 200 см³ V = 200·10^-6 м³=2·10^-4 м³

η = 0,001 Па·с η = 0,001 Па·с

Re_кр = 3000 Re_кр = 3000

Знайти: D - ?

Розв`язування:

Оскільки в задачі йдеться про діаметр труби, при якому ще зберігається ламінарність потоку, то скористуємось критичним значення чила Рейнольдса.

Для Re_кр маємо:

Re_кр= (1),

де υ – швидкість потоку,

ρ – густина води (ρ = 10³ кг/м³).

.

Невідому за умовами задачі швидкість знайдемо із формули для об’єма речовини, що протікає через поперечний перетин труби за час t:

V=Sυt.

Враховуючи, що - площа поперечного перетину труби, маємо для швидкості:

(2).

Підставимо (2) в (1):

.

Отримаємо вираз для D:

.

Знайдемо чисельне значення D:

.

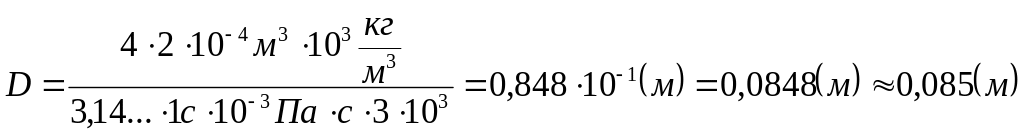Дії з одиницями виконаємо для наочності окремо:

.

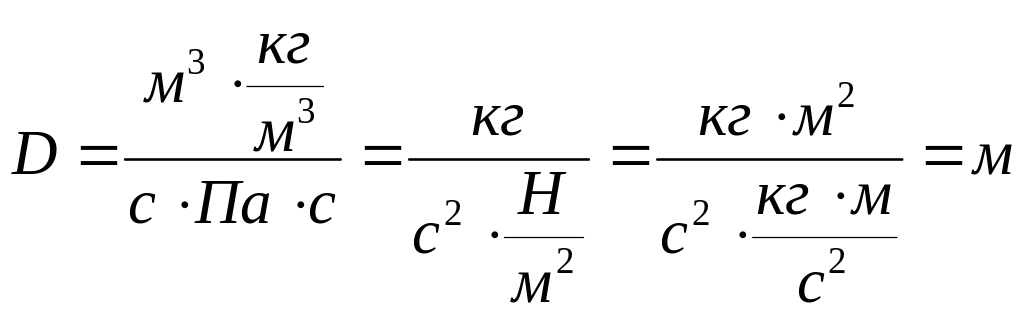Таким чином маємо: D ≤ 0,085м.

Відповідь: для збереження ламінарності потоку діаметр труби не

повинен перевищувати значення 0,085м.

ЗАДАЧА 3

Вважаючи, що ламінарність руху рідини (або газу) в циліндричній трубі зберігається при Re ≤ 3000, показати, що умови попередньої задачі відповідають ламінарній течії потоку. Кінематичну в’язкість газу прийняти за . (В якості характерного параметра l взяти діаметр труби.)

Дано:

υ = 0,12 м/с

d = 2 см= м

Знайти: Re - ?

Розв`язання:

Для числа Рейнольдса маємо:

Підставимо чисельні дані попередньої задачі і перевіремо, чи відповідає значення Re умові Re ≤ 3000:

.

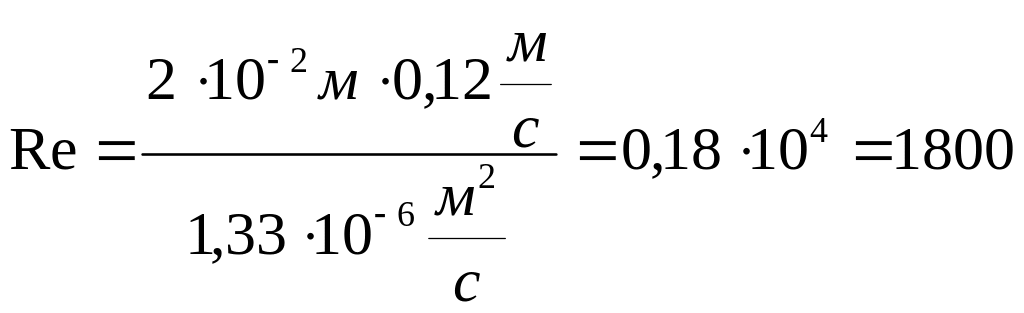Відповідь: оскільки 1800 < 3000, то потік можна вважати

ламінарним.

Рекомендована література

1 Курс загальної фізики. Т.1 (І.В.Савєльєв) – М., Наука, 1973. – 1472 с.; § 54, §58-60 2 Фізика. (П.П.Чолпан) – К., Вища школа, 2003. – 567 с.; § 3.1-3.3