2. Модифікований алгоритм

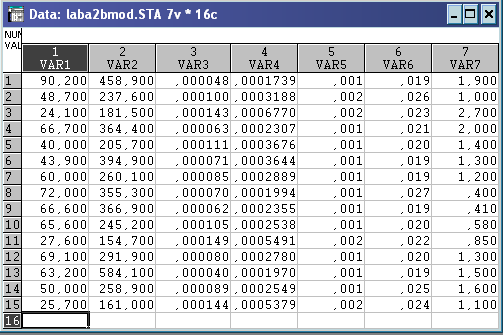
1) Утворення матриці вихідних даних

2. Розділення ознак на:

x₁, x₂, x₇ – стимулятори;

x₃, x₄, x₅, x₆ – де стимулятори;

Всі ознаки-симптоми, які є де стимуляторами, необхідно перетворити таким чином:

.

3. Зважування ознак-симптомів не проводиться.

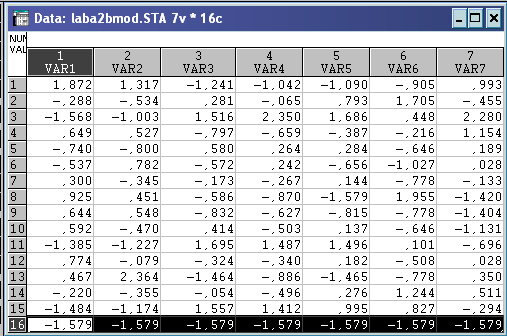
4. Перехід до матриці стандартизованих ознак Z. Задання анти еталону( точка додається до матриці в якості 16 об’єкта (рядок 16)).

Серед усіх стандартизованих ознак-симптомів визначають найменше значення – z^٭(-1,579; -1,579; -1,579; -1,579; -1,579; -1,579; -1,579) – точка анти еталону.

Стандартизовані дані та точка антиеталону:

3. Вибір метрики відстані – Евклідова метрика.

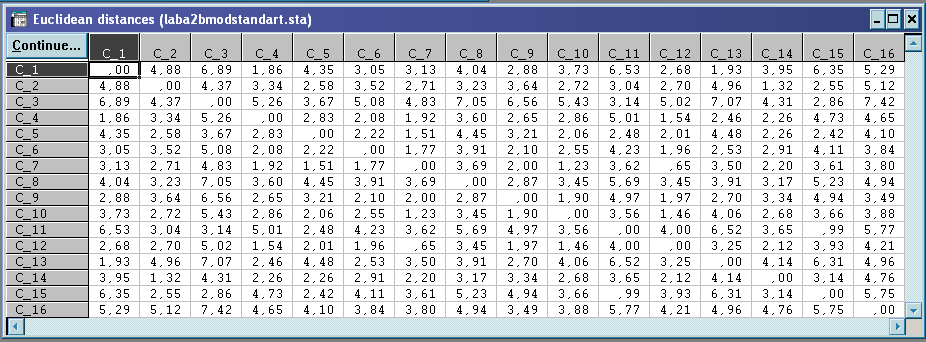
3. Розрахунок міри схожості (в Excel) за формулою:

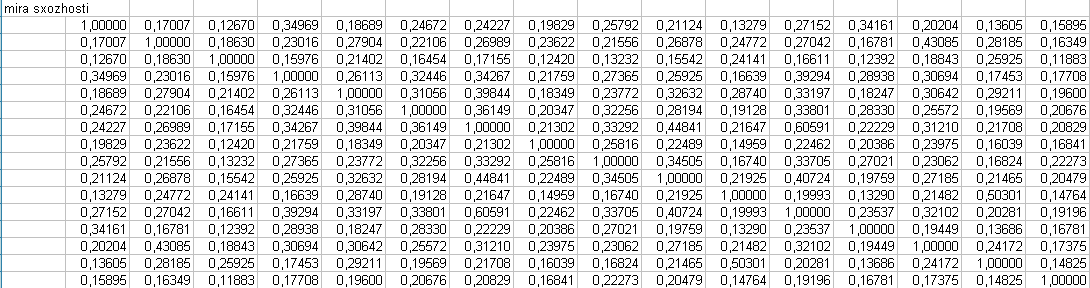
3. Нормування за формулою

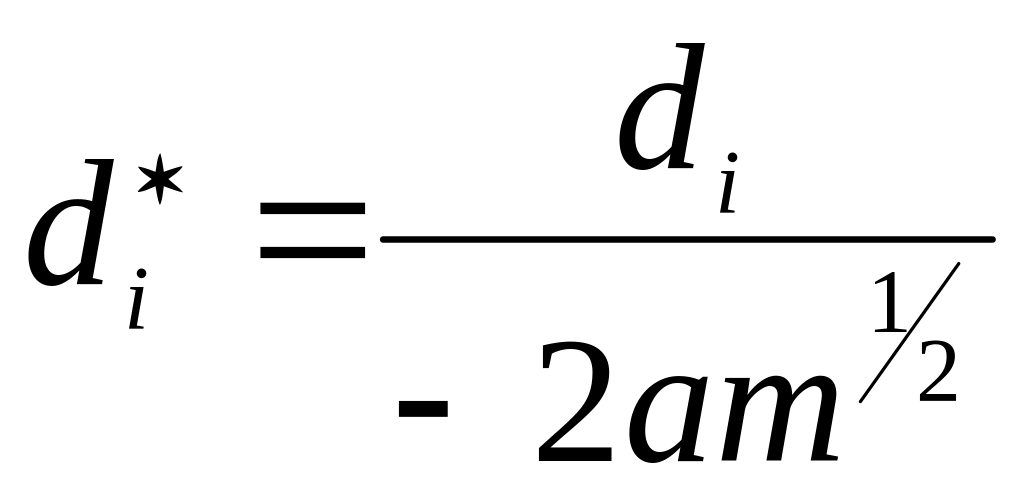
значень відстаней(в Excel) і присвоєння відповідних їм рангів.

Значения можна розглядати в якості шуканого латентного показника «Інвестиційна привабливість» об’єктів приватизації на досліджуваній сукупності підприємств.

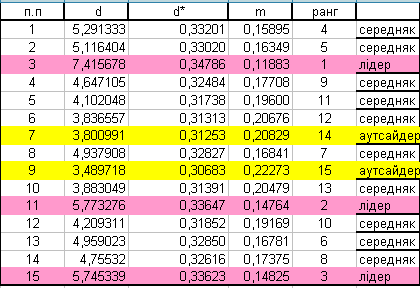
Лідери (3, 11, 15 підприємства) мають найближчу відстань до еталону.

Аутсайдери (7, 9 підприємства) мають мінімальну схожість з еталоном.

Середняки – підприємства, які займають проміжне значення.

Результати оцінки «Інвестиційна привабливість» об’єктів приватизації за модифікованим алгоритмом:

Порівняння результатів багатовимірної оцінки «Інвестиційна привабливість» об’єктів приватизації:

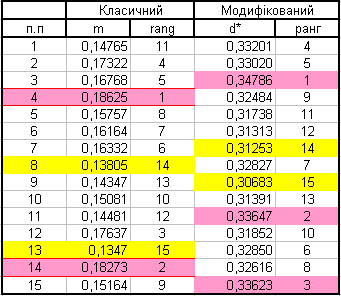
Висновок:

Порівняння оцінок показує, що вони різні. В класичному алгоритмі ті що були лідерами та аутсайдерами стали посередніми. В модифікованому алгоритмі ми бачимо нових лідерів та нових аутсайдерів.

Завдання 3:

Здійснити багатовимірне групування вихідної статистичної сукупності об’єктів за допомогою кластерного аналізу на основі:

1. ієрархічного агломеративного алгоритму;

2. методу k-середніх, вважаючи, що k=R з попереднього пункту;

3. алгоритму «Форель».

Проаналізувати одержані результати й поглибити зроблені висновки за допомогою методу подвійного об’єднання та оптимізаційних процедур.

Зробити порівняльний аналіз використаних алгоритмів кластерного аналізу й перевірити статистичні гіпотези відносно однорідності досліджуваної сукупності об’єктів.

Виконання:

Запуск системи STATISTICA

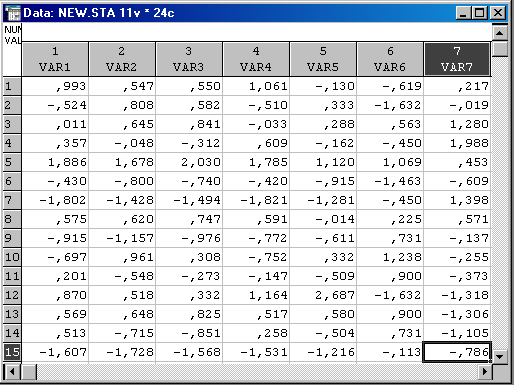
2. Вихідні дані:

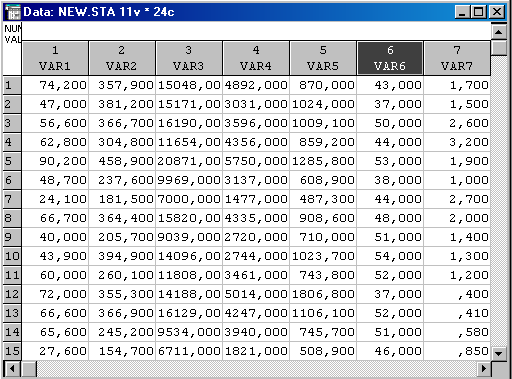
2. Стандартизація даних – приведення змінних до одного безрозмірного вигляду. Така процедура виражається формулою:

Cluster Analysis: Виділяємо масив вихідних даних, клацаємо правою кнопкою миші. Вибираємо Fill(Standardize Block →Standardize Columns);

А) Ієрархічний агломеративний алгоритм.

Вибір модуля «Кластерний аналіз»(Cluster Analysis) → «Методи кластерізації»(Clustering Method) → «Об’єднання (дерево кластерізації)»(Joining(tree clustering)) → Ok →

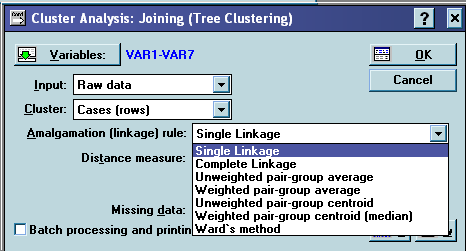
→ вибираємо критерій агломерації і метрику відстані →Ok→ «Результати об’єднання»(Joining Results) → Вертикальна ієрархічна дендограма (Vertical icicle plot). Більш точну інформацію можна отримати, натиснувши кнопку вікна результатів «Послідовність агломерації»(Amalgamation schedule).

• На основі критерію ближнього сусіда і евклідової відстані.

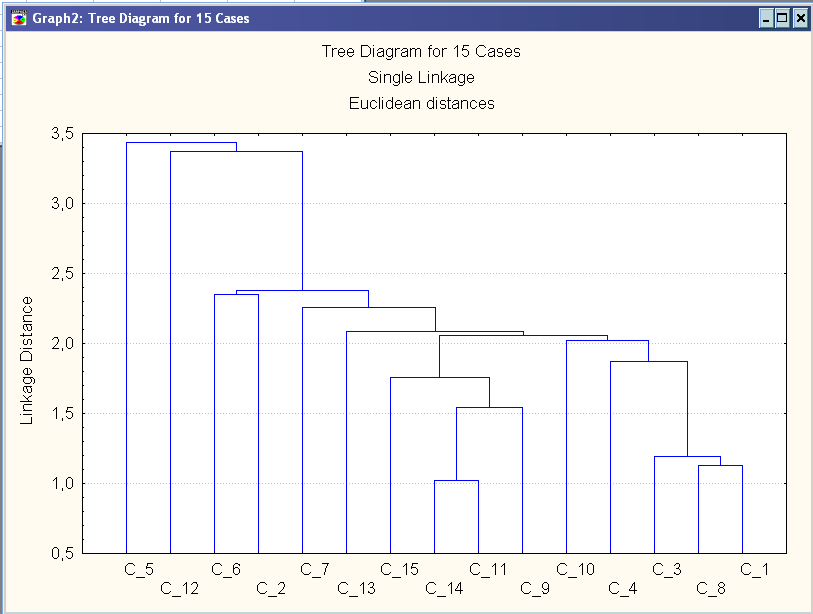
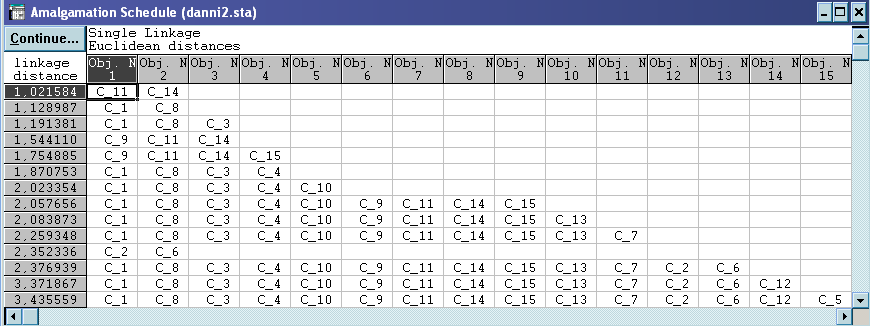
Маємо таке розбиття:

3 згущення об’єктів – кластери (11,14,9,15) (1,8,3,4,10) (2,6), а також 4 об’єкти, віддаленні від інших – самостійні кластери (5) (12) (7) (13).

• На основі критерію середнього зв’язку і квадрат евклідової відстані

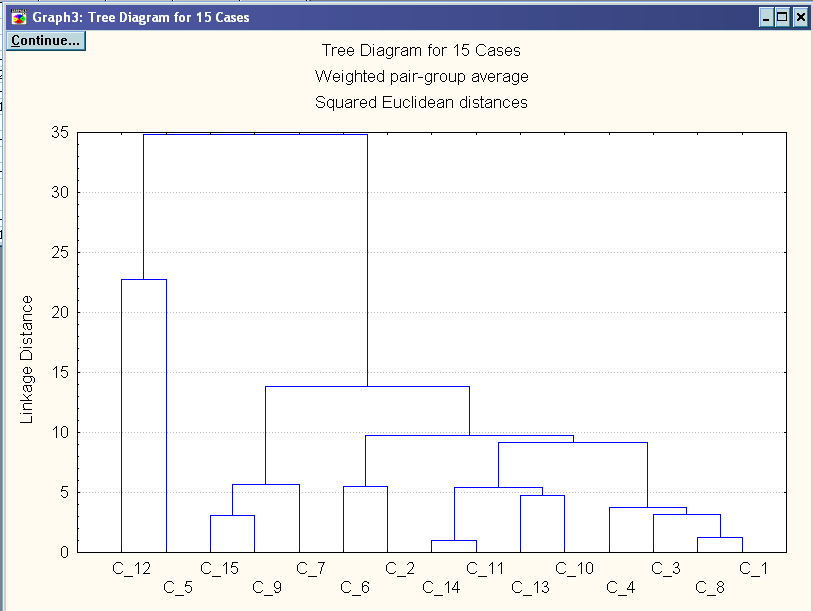
Маємо таке розбиття:

6 згущень об’єктів – кластери (11,14) (1,8,3,4) (9,15,7) (10,13) (2,6) (5,12).

• На основі критерію віддаленого сусіда і лінійної відстані

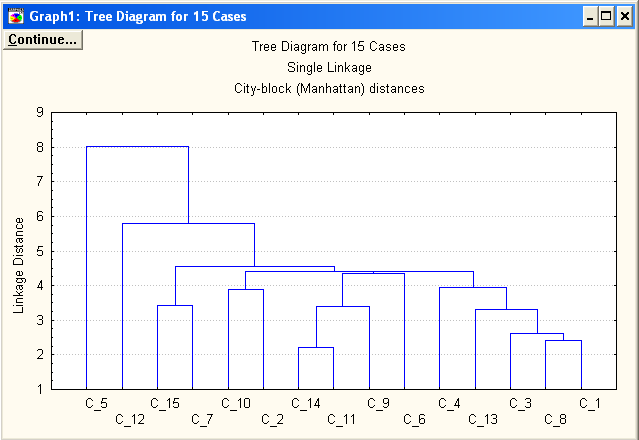
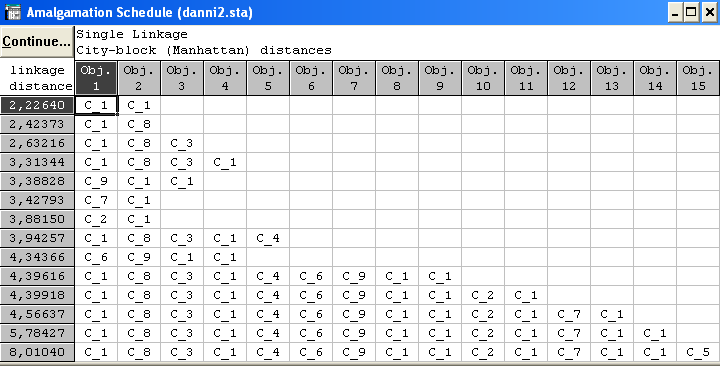
Маємо таке розбиття:

6 згущень об’єктів – кластери (11,14,9,6) (1,8,4) (7,15) (2,10) (3,13) (5,12).

Таким чином, в результаті багатовимірного групування об’єктів на основі ієрархічного агломеративного алгоритму кластерного аналізу, побудованого за трьома критеріями для знаходження оптимального і більш стійкого розбиття, можна зробити висновок, що дану сукупність магазинів можна розбити на 6 кластерів – (11,14,9,6) (1,8,4) (7,15) (2,10) (3,13) (5,12).

Б) Метод k – середніх.

Вибір модуля «Кластерний аналіз»(Cluster Analysis) → «Методи кластерізації»(Clustering Method) → «Метод k – середніх»(k - means clustering)) → Ok →

Ok → «Результати методу k-середніх, вважаючи, що k=R=6» (k-Means Clustering Results)

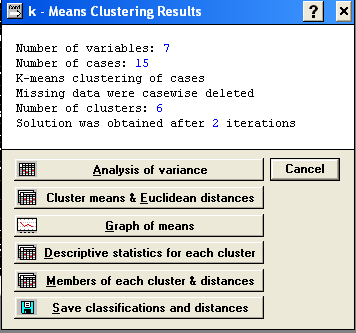
Натиснення на кнопку – Save classification and distances – зберігає матрицю класифікації і відстаней розбиття кластерів. Можна побачити в який кластер входять об’єкти і відстані між кластерами.

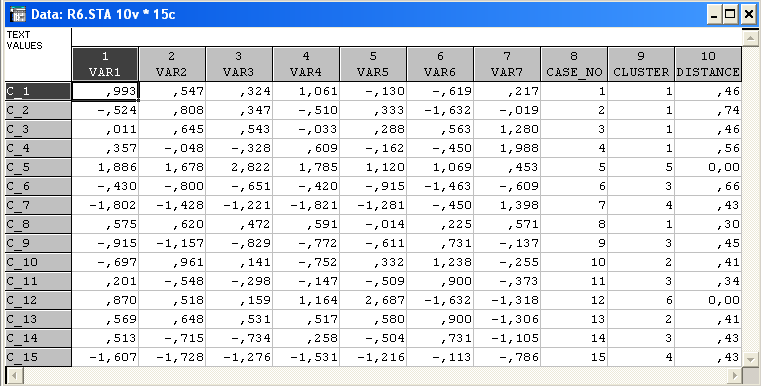
Маємо таке розбиття:

4 згущення об’єктів – кластери (1,2,3,4,8) (10,13) (6,9,11,14) (7,15), а також 2 об’єкти, віддаленні від інших – самостійні кластери (5) (12).

Очевидно, що розбиття об’єктів внаслідок застосування методу k-середніх, вважаючи, що k=R=6 з попереднього пункту, не співпадає з багатовимірною класифікацією цих об’єктів на основі ієрархічного агломеративного алгоритму кластерного аналізу.

В) Алгоритм «Форель»

Аналіз матриці евклідової відстані між об’єктами показує,

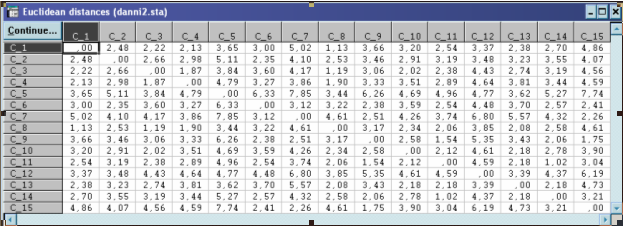
що .

Гіперсфера, радіуса Т=1,02, виділить рівно 15 кластерів, які вмістять в себе по одному об’єкту, а гіперсфера, радіуса Т=3,9 виділить всю вихідну сукупність – 1 кластер, що буде містити всі 15 об’єктів. Тоді, в якості радіусу гіперсфери значення T з інтервалу [1,02; 3,9] візьмемо T=2.

Розрахунок координат центра ваги утвореної сукупності проводиться в Excel за формулою середнього арифметичного.

Приймаємо точку за новий центр гіперсфери і утворюємо нову матрицю стандартизованих даних.

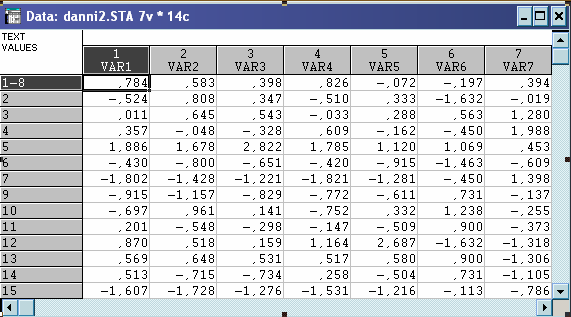
Щоб визначити, які точки потрапили в середину гіперсфери з центром в точці , знаходимо евклідову відстань.

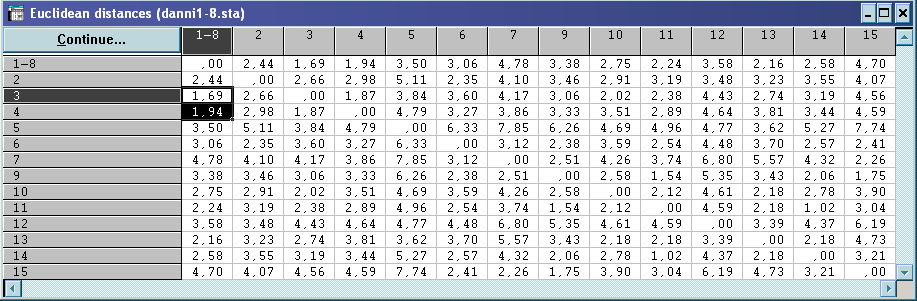
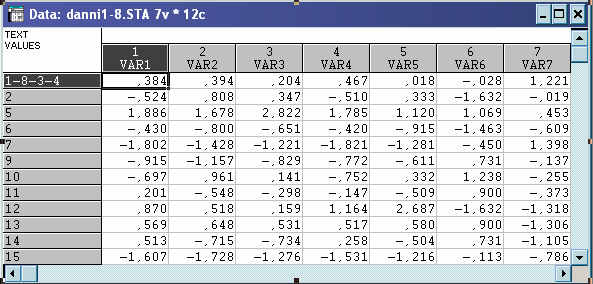
Приймаємо точку за новий центр гіперсфери і утворюємо нову матрицю стандартизованих даних.

Щоб визначити, які точки потрапили в середину гіперсфери з центром в точці , знаходимо евклідову відстань.

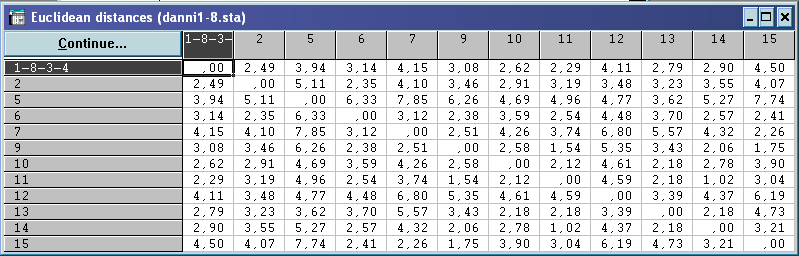
Всі – жоден новий об’єкт не потрапив в середину гіперсфери. Об’єкти №№1, 8, 3, 4 утворюють кластер типу таксон і із подальшого аналізу виключаються.

Із об’єктів, що залишилися вибираємо знову довільну точку №4 в ролі вихідного центра гіперсфери. Аналіз проводимо аналогічно.

Матриця стандартизованих даних:

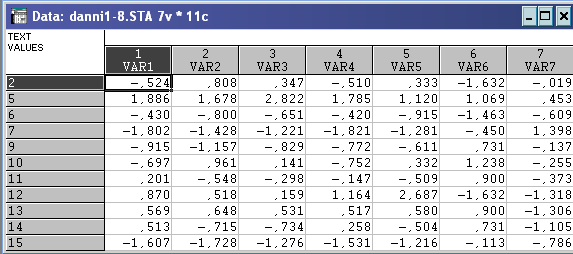
Евклідова відстань:

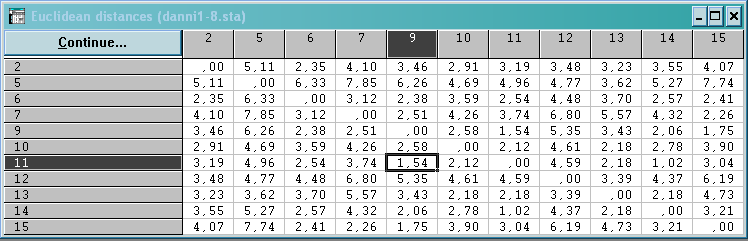
– №11 потрапив в середину гіперсфери.

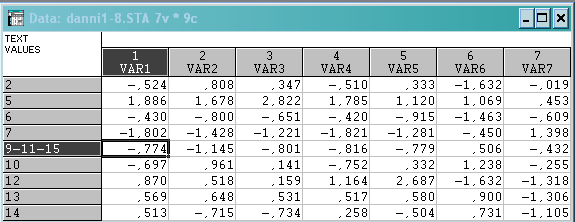
Матриця стандартизованих даних:

Евклідова відстань:

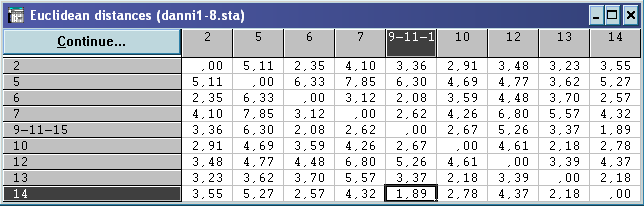
– №14 потрапили в середину гіперсфери.

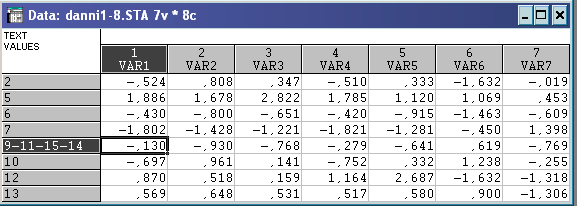
Матриця стандартизованих даних:

Евклідова відстань:

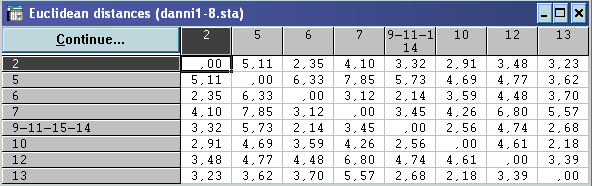
Всі і=9, 11, 15, 14 – жоден новий об’єкт не потрапив в середину гіперсфери. Об’єкти №№ 9, 11, 15, 14 утворюють кластер типу таксон і із подальшого аналізу виключаються.

Аналіз рядків 2, 5, 6, 7, 10, 12, 13 таблиці евклідових відстаней показує, що відповідні об’єкти . прийняті за вихідні центри ваги гіперсфери, радіусу Т=2, також утворюють окремі кластери, так як жодна з точок не потрапляє в середину неї.

Таким чином, алгоритм «Форель» приводить до такого розбиття вихідної сукупності об’єктів: (1,8,3,4)(9,11,15,14)(2)(5)(6)(7)(10)(12)(13), що дещо не співпадає(але є близьким) з результатами, отриманими за допомогою оптимізаційного та ієрархічно-агломеративного алгоритмів.

Але аналіз даних за допомогою алгоритму «Форель» є достатньо стійким.

Порівняльний аналіз різних методів класифікації

з оптимізаційним алгоритмом.

На основі функціоналу ,здійснимо порівняльний аналіз якості довільного розбиття 15 об’єктів на R кластерів (R=6) з якістю найкращого їх групування, отримані раніше за різними методами класифікації за результатами:

• Ієрархічного агломеративного алгоритму :

(11,14,9,6) (1,8,4) (7,15) (2,10) (3,13) (5,12)

• Методу k-середніх:

(1,2,3,4,8) (10,13) (6,9,11,14) (7,15)(5)(12)

• Методу «Форель»:

(1,8,3,4)(9,11,15,14)(2)(5)(6)(7)(10)(12)(13)

А) Нехай довільне розбиття точок на R=6 кластерів має вигляд:

(1,2)(3,4)(5,6,7)(8,9,10)(11,12)(13,14,15).

Розраховуємо квадрати евклідових відстаней між всіма точками:

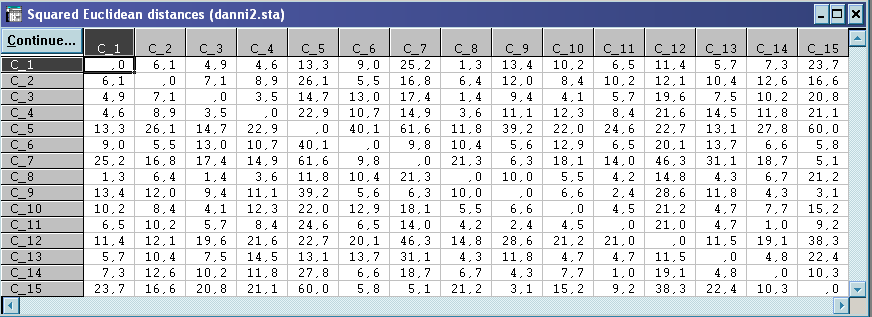
На основі суми квадратів попарно-внутрішньо кластер них відстаней між об’єктами, маємо – для довільного розбиття.

Порівняння знайдених значень функціоналів якості розбиття, на основі методу «Форель» і оптимізаційного методу, показує

< .

Тобто, з точки зору цільової функції слід віддати перевагу результату багатовимірної класифікації, а саме методу «Форель».

Б) Нехай довільне розбиття точок на R=8 кластерів має вигляд:

(1)(2)(3,4,5)(6,7,8)(9,10)(11)(12,13)(14,15).

На основі суми квадратів попарно-внутрішньо кластер них відстаней між об’єктами, маємо – для довільного розбиття.

Порівняння знайдених значень функціоналів якості розбиття, на основі методу k-середніх, ієрархічного агломеративного алгоритму і оптимізаційного методу, показує

<

Тобто, з точки зору цільової функції слід віддати перевагу результату багатовимірної класифікації, а саме методу k-середніх.

Таким чином, можна віддати перевагу розбиттю об’єктів, що зроблені за методом k-середніх та методом «Форель», оскільки їх функціонали приймають менші значення.

Подвійне об’єднання.

Вибір модуля «Кластерний аналіз»(Cluster Analysis) → «Методи кластерізації»(Clustering Method) → «Подвійне об’єднання »(Two-way joining) → Ok →

На основі матриці стандартизованих даних.

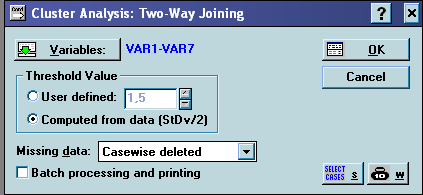
Панель результатів:

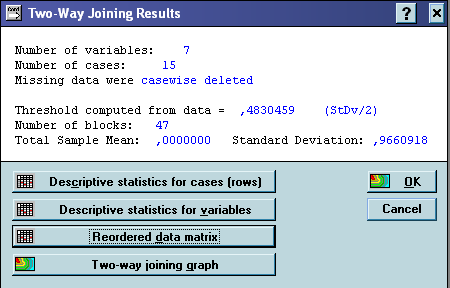
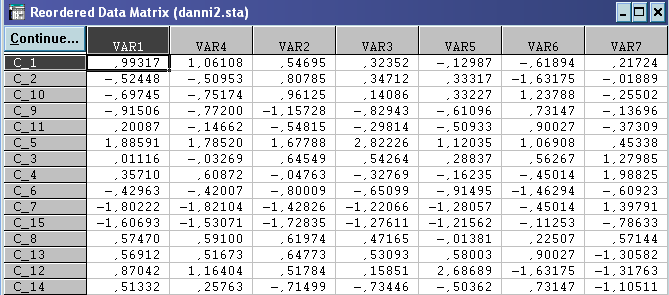
Утворилося 47 блоків. Матриця перегрупованих даних має вигляд:

Якщо збільшити порогові значення, тоді кількість утворених блоків зменшиться, наприклад: User defined=3

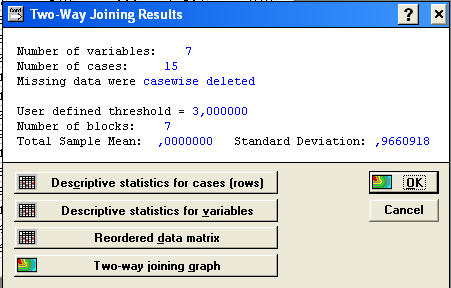
Панель результатів:

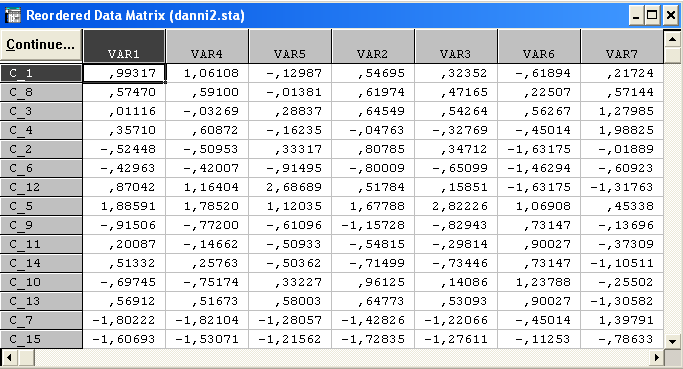
Утворилося 7 блоків. Матриця перегрупованих даних має вигляд:

Перевірка гіпотез однорідності сукупності об’єктів

{об’єкти, розглянутої групи, узяті з однорідної генеральної сукупності};

{об’єкти, розглянутої групи, узяті з різних генеральних сукупностей}.

• Розглянемо розбитя об’єктів, отримані раніше за ієрархічним агломеративним алгоритмом :

(11,14,9,6) (1,8,4) (7,15) (2,10) (3,13) (5,12)

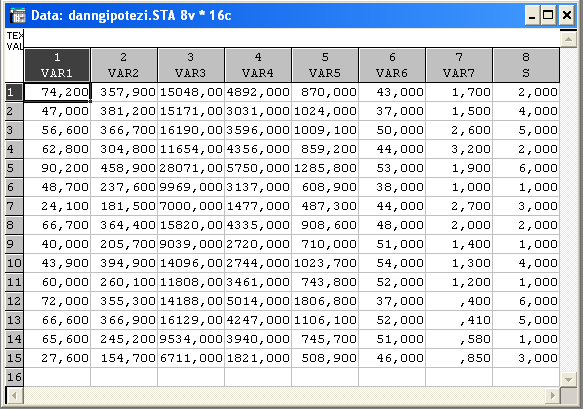
S – додаткова групуючи зміна, яка вказує на належність об’єкта до певного кластера.

Вибір модуля «Дискримінантний аналіз»(Discriminant Analysis) → Startup Panel → Stepwise Discriminant Function Analysis →

Ok → Model definition → Discriminant Function Analysis Result →

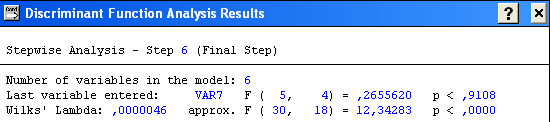
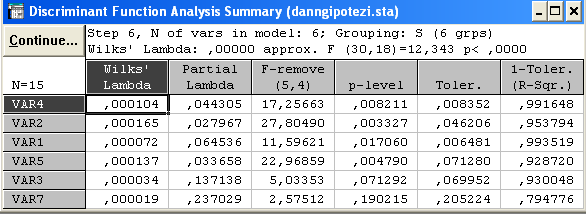
Можна стверджувати, що отримане розбиття вихідної сукупності об’єктів є обґрунтоване, з достовірністю 99, 99999% =(1-0,0000)*100 > 95% .

x4, x2, x1,x5,x3,x7 – пояснюють головні відмінності кластерів.

p< 0 .0000; - мале

• Розглянемо розбитя об’єктів, отримані раніше за методом k-середніх:

(1,2,3,4,8) (10,13) (6,9,11,14) (7,15)(5)(12)

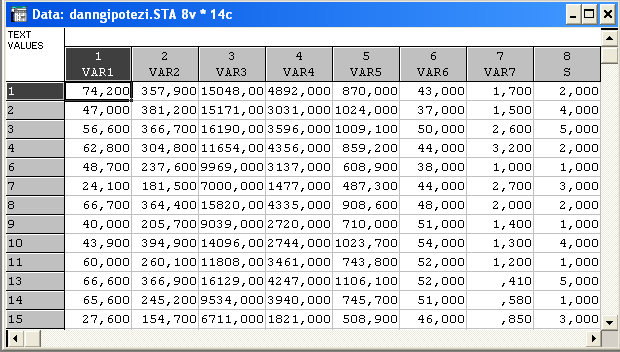
S – додаткова групуючи зміна, яка вказує на належність об’єкта до певного кластера.

Вибір модуля «Дискримінантний аналіз»(Discriminant Analysis) → Startup Panel → Stepwise Discriminant Function Analysis → Ok → Model definition → Discriminant Function Analysis Result →

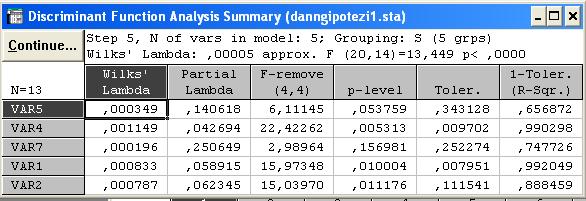
Можна стверджувати, що отримане розбиття вихідної сукупності об’єктів є обґрунтоване, з достовірністю 99, 88% = (1-0,0012)*100 > 95% .

x5, x4, x7, x1,x2 – пояснюють головні відмінності кластерів.

p< 0, 0000; - мале .

• Розглянемо розбитя об’єктів, отримані раніше за методом «Форель»:

(1,8,3,4)(9,11,15,14)(2)(5)(6)(7)(10)(12)(13)

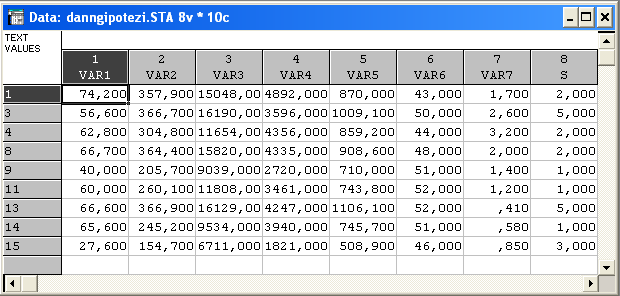
S – додаткова групуючи зміна, яка вказує на належність об’єкта до певного кластера.

Вибір модуля «Дискримінантний аналіз»(Discriminant Analysis) → Startup Panel → Stepwise Discriminant Function Analysis → Ok → Model definition → Discriminant Function Analysis Result →

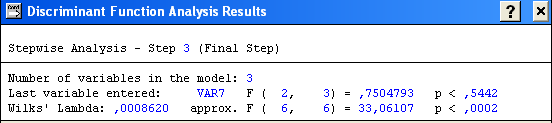
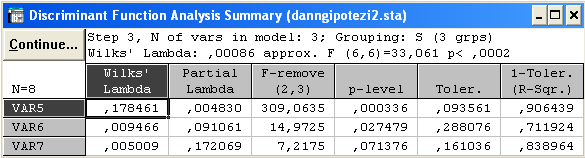
Можна стверджувати, що отримане розбиття вихідної сукупності об’єктів є обґрунтоване, з достовірністю 99, 7% = (1-0,0030)*100 > 95% .

x5, x6, x7 – пояснюють головні відмінності кластерів.

p< 0, 0002; – мале.

Отже, всі розбиття об’єктів є статистично надійними. Малі значення Лямбди Уілкса, свідчать про успішне обґрунтоване розбиття вихідної сукупності об’єктів. Гіпотеза {об’єкти, розглянутої групи, узяті з однорідної генеральної сукупності} приймається.