Коротков Е.Б,

Информационные устройства и системы.

Ч.3 Локационные системы.

Локационные информационные системы (ЛС) относятся к устройствам бесконтактного действия и реализуют бионическую функцию слуха. Ин­формативным параметром этих систем является модулированная волна различной физической природы, характеристики которой определяются ин­тегральными свойствами среды распространения. В робототехнике и меха­тронике ЛС используют для определения координат и скорости объектов в задачах управления и навигации, для обеспечения необходимой траектории движения исполнительного механизма вблизи границы раздела сред, а так­же в качестве средств безопасности. Отдельной областью их применения является определение свойств среды распространения. Во всех случаях пре­образователи ЛС являются датчиками среды. Поскольку и система, и объект находятся в некотором физическом поле, результаты измерения существен­но зависят от его свойств. В зависимости от пространственно-временных свойств среды различают потенциальные (например, электростатические) и вихревые (электромагнитные и акустические) поля. Как правило, вихревые поля содержат больше параметров, пригодных для измерения, и поэтому более информативны. Тем не менее иногда (например, при работе на малых расстояниях) целесообразно использовать ЛС, принцип действия которых основан на свойствах потенциальных полей Однако в любом случае необ­ходимые данные получают из переносимой полем информации об объекте.

ЛС подразделяют по трем основным признакам:

по физической природе носителя информации — электромагнитные, акустические, оптические, пневматические, электрические и магнитные;

по способу локации — активные и пассивные;

по типу модулирующей функции — непрерывные и импульсные.

Активные ЛС регистрируют отраженный эхо-сигнал, в то время как пассивные воспринимают собственное излучение объекта. Примером ак­тивной ЛС является акустический дальномер, пассивной — вихретоковая система.

Теоретические основы локации

Общие сведении

Движение волны, представляющее собой колебательный процесс рас­пространения возмущения в некоторой среде, происходит с конечной скоро­стью с и описывается волновым уравнением вида

, где u — амплитуда возмущения; х, у, z — ортогональные оси координат.

В волновой теории наиболее известным является частотное уравнение

Механизм распространения волн в среде связан с явлениями отражения, дифракции, рефракции (искривление луча вследствие преломления), погло­щения, рассеяния и различен для разных длин волн. Особенно наглядно это проявляется в области радиочастот, которые широко используются в нави­гационных системах мобильных роботов. Так, волны сверхдлинного диапа­зона (А, > 10 км) сравнительно слабо поглощаются земной корой, а на их распространение существенно влияет ионосфера, которая вместе с поверх­ностью Земли образует сферический волновод. Длинные волны

(к = 1... 10 км), напротив, сильно поглощаются Землей и хорошо ее огибают; это происходит вследствие дифракции и волноводного эффекта, присущего волнам данного диапазона. Средние волны (X = 100... 1000 м) значительно поглощаются ионосферой днем и распространяются только благодаря ди­фракции (так называемые земные волны). Ночью ионосферные отражения улучшаются, и дальность волн резко возрастает (эти волны получили назва­ние пространственных). Что касается коротких волн (X = 10... 100 м), то ди­фракция у них выражена слабо, однако благодаря ионосферному отражению они могут достигать точки антипода. В диапазоне X = 10... 100 м сильно проявляются дисперсионные свойства ионосферы, а для наиболее коротких волн она и вовсе прозрачна. Ультракороткие волны (X = 1 мм ... 10 м) рас­пространяются практически прямолинейно, а на их дальность влияет зату­хание колебаний в тропосфере и стратосфере Земли Диапазон ультракорот­ких волн делят на четыре поддиапазона: метровый, дециметровый, санти­метровый и миллиметровый. Дальность распространения метровых волн достигает 2000 км, сантиметровые волны рассеиваются и поглощаются об­лаками и туманом, а миллиметровые — газами атмосферы. Так как даль­ность распространения санти- и миллиметровых волн невелика, то в систе­мах передачи информации этих диапазонов применяют волноводы и другие направляющие устройства.

Под затуханием будем понимать некоторую интегральную характери­стику, которая связана с потерей энергии колебаний в среде, приводящей к ослаблению амплитуды сигнала. Затухание сигнала влияет на дальность его распространения. В линейных системах с одной степенью свободы ампли­туда и колебаний убывает с расстоянием х по экспоненциальному зако­ну. Теоретиче­ски затухание длится бесконечно долго, однако на практике колебательный процесс считают закончившимся, если его амплитуда составляет 1% от на­чальной, т. е. =0,01, или х = 4,6/ζ.

Зная коэффициент затухания, можно определить глубину проникновения электромагнитных волн в среду. Так, для морской воды коэффициент затухания

ζ.= — , где μ,ρ — соответственно магнитная проницаемость и удельное электросопротивление морской воды; — магнитная постоян­ная. Глубина проникновения δ, при которой амплитуда сигнала уменьшает­ся в с раз, определяется выражением δ= 1/е. Следовательно, при частоте электромагнитного сигнала f = I кГц (λ = 300 м), ρ = 0,25 Ом • м и μ = 1 глубина проникновения б = 8 км. В металлических предметах затухание значительно сильнее. Так, в стали (р ~ 7 -10 Ом • м, 10 ) глубина

проникновения б составляет доли миллиметра.

В инженерных расчетах для определения затухания сигнала также ис­пользуют интегральный параметр, называемый коэффициентом ослабления где Р пр, Ризл — мощность сигнала на входе приемника и на выходе излу­чателя соответственно.

Ослабление сигнала зависит от расстояния / между приемником и излу­чателем (или объектом) и свойств среды. Так, для изотропной среды, когда волна имеет сферическую форму, мощность сигнала на входе приемника

убывает пропорционально I² . Например, в пассивной ЛС, где волна прохо­дит расстояние до объекта один раз,

Р_пр=К_ослРизл = k_рР_изл / l²

В активной ЛС (например, в импульсном дальномере) волна дважды проходит путь до объекта, поэтому ослабление сигнала будет в четыре раза больше. Для таких систем дальность определится выражением

/ = сΔt/ 2,

где Δt — время прохождения сигнала от момента излучения до момента приема.

Направленность излучении

Эффективность ЛС в значительной степени определяется надежностью локации (точностью обнаружения сигнала, помехоустойчивостью связи и др.) и дальностью ее распространения. Поэтому при посылке информаци­онных сигналов используют направленные модулированные излучения.

Направленность излучателя (приемника) ЛС — это свойство, заклю­чающееся в наличии некоторой пространственной избирательности, т. е. способности излучать (принимать) волны в одних направлениях в большей степени, чем в других. Направленность преобразователя позволяет увели­чить соотношение сигнал/шум как в режиме излучения, так и в режиме приема сигнала.

В режиме излучения направленность определяется интерференцией ко­лебаний, приходящих в данную точку среды от отдельных (малых по срав­нению с длиной волны в среде) участков излучателя. Для направленного излучения необходимо выполнение неравенства d_хар/λ >> 1, где d_хар/λ — параметр, называемый волновым размером излучателя;

d_хар — характерный размер излучателя (например, его диаметр).

В режиме приема сигнала направленность вызывается интерференцией электрических напряжений, развиваемых на выходных клеммах отдельных элементов приемника.

В общем случае диаграммы направленности излучателя и приемника ЛС отличаются. Это характерно, например, для оптических ЛС. Если же в сис­теме используются обратимые преобразователи, например в акустических ЛС, то их диаграммы направленности в режимах приема и излучения пола­гают одинаковыми.

Направленность — важнейшая характеристика локации, обеспечивающая саму возможность свяли. В живой природе она реализуется при фокусировке сигнала вследствие интерференции его составляющих, излучаемых несколькими источника­ми. У летучей мыши такими источниками являются две ноздри, расстояние между которыми приблизительно соответствует 2А, излучаемого звука Ширина диаграммы направленности излучающего аппарата летучей мыши составляет 30...50°, приемного — 1…50. Указанное обстоятельство обеспечивает высокую разрешающую способ­ность ее локационного аппарата и позволяет различать проволоку толщиной 0,2 мм, натянутую на расстоянии всего 5 мм от плоской отражающей поверхности. Высокая разрешающая способность характерна и для навигациохшой системы дель­фина, который обнаруживает шарик диаметром 3 мм на расстоянии 5 м.

Наиболее простая математическая модель, описывающая излучатель, ос­нована на его представлении в виде дискретной или непрерывной совокуп­ности малых по сравнению с длиной волны излучающих элементов, а поле излучателя определяется суммированием сферических волн, создаваемых отдельными элементами. Общие теоретические методы описания направ­ленности излучения основываются на использовании функций Грина, позволяющих учесть геометрические характеристики излучателя и излучае­мою сигнала. Однако для преобразователей произвольной формы эти ха­рактеристики трудно определить из-за сложности формы поля вблизи излу­чающей поверхности

Направленность излучателя (приемника) ЛС описывается двумя пара­метрами- характеристикой направленности и коэффициентом концентрации.

Характеристикой направленности преобразователя называется выраже­ние вида

D(r) = P(r)/Р(r₀),

где Р(r), Р(r₀)— мощности фиксируемых на одинаковом расстоянии от центра преобразователя сигналов в направлениях, характеризуемых радиус-векторами

г и го соответственно. Обычно радиус-вектор го выбирают таким, чтобы его направление совпадало с направлением максимума излучения или максимума чувствительности. В графическом виде характеристика D(r) представляет собой пространственную или плоскую диаграмму направленности, отображаемую в полярных или декартовых координатах (рис. 5.1, а). Аргументом диаграммы направленности, как правило, является угол 0, отсчитываемый от направления ОА максимального излучения (см. рис. 5.1, а) и зависящий от частоты сигнала. Направление ОА обычно совпадает с одной

из осей преобразователя.

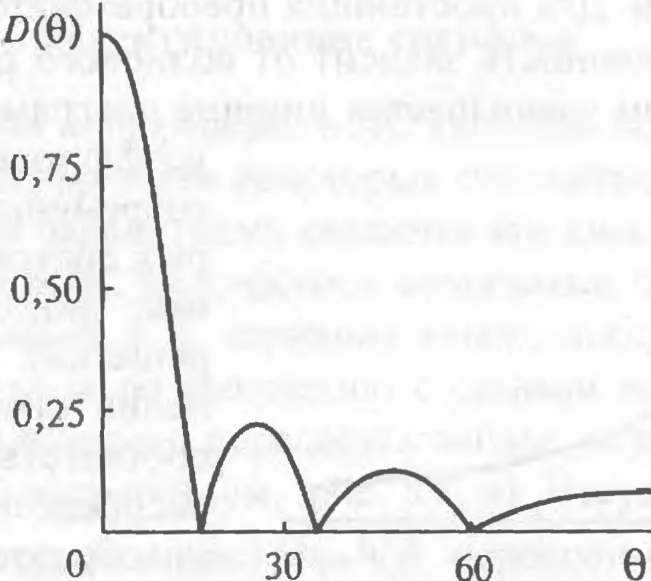
Диаграмма направленности в полярной (а) и в декартовой (б) сис­темах координат (ОА — направление главного максимума, 60707 — угловая ширина главного максимума по уровню 0,707)

Диаграмма направленности характеризуется: главными и добавочными максимумами (лепестками); угловой шириной главного максимума; отно­шениями амплитуд добавочных максимумов к главному.

Угловую ширину главного максимума определяют двумя способами. В первом она равна углу θ₀ между направлениями нулевого излучения, во

втором — углу θ_0.707 между направлениями излучения по уровню 0,707,

соответствующему 50 %-ной излучаемой мощности.

Лепестковый характер диаграммы направленности излучателя связан с интерференцией воли, излучаемых отдельными элементами. В главном ле­пестке диаграммы может сосредоточиваться свыше 90 % всей мощности излучателя. Простейшим излучателем является магнитный диполь — виток провода, диаметр которого мал по сравнению с длиной излучаемой волны. Диаграмма направленности диполя имеет форму гороида. Направленности реальных преобразователей в горизонтальной и вертикальной плоскостях обычно различаются. Так, в радиолокационных системах сантиметрового диапазона диаграмма узкая в горизонтальной плоскости и широкая в верти­кальной.

Коэффициент концентрации, или коэффициент направленного действия

АГад характеризует меру концентрации излучаемой энергии вдоль некоторо­го направления (обычно направления главного максимума диаграммы на­правленности) определяется выражением вида

К_нд=Р_max /P

где Ртах — мощность сигнала в направлении главного максимума на некотором расстоянии l от излучателя; Р — мощность сигнала гипо­тетического «ненаправленного» излучателя на том же расстоянии. Под ненаправленным понимается излучатель с диаграммой направленности в

форме шара. Для простейших преобразователей ЛС (диполей) К_нд = 1,5.

Направленность зависит от волнового размера d _xар/λ - излучателя. С его увеличением уменьшается ширина диаграммы направленности и возрастает

коэффициент концентрации. В современных ЛС, преобразователи кото­рых состоят из большого числа элементар­ных диполей (так называемые антенные решетки), существует возможность управ­ления диаграммой направленности путем соответствующего амплитудно-фазового распределения излучения по поверхности преобразователя. Так, уменьшая мощность излучения Р(х) отдельных диполей от центра излучающей поверхности к ее краю, можно расширить главный максимум диаграммы направленности и уменьшить добавочные максимумы. Если же увеличивать мощность излучения Р(х) диполей к краю излучающей повер­хности, можно сформировать более острую диаграмму направленности. Изменяя фазу излучения отдельных диполей, можно поворачи­вать главный максимум диаграммы направленности, т. е. осуществлять сканирование среды излучения.

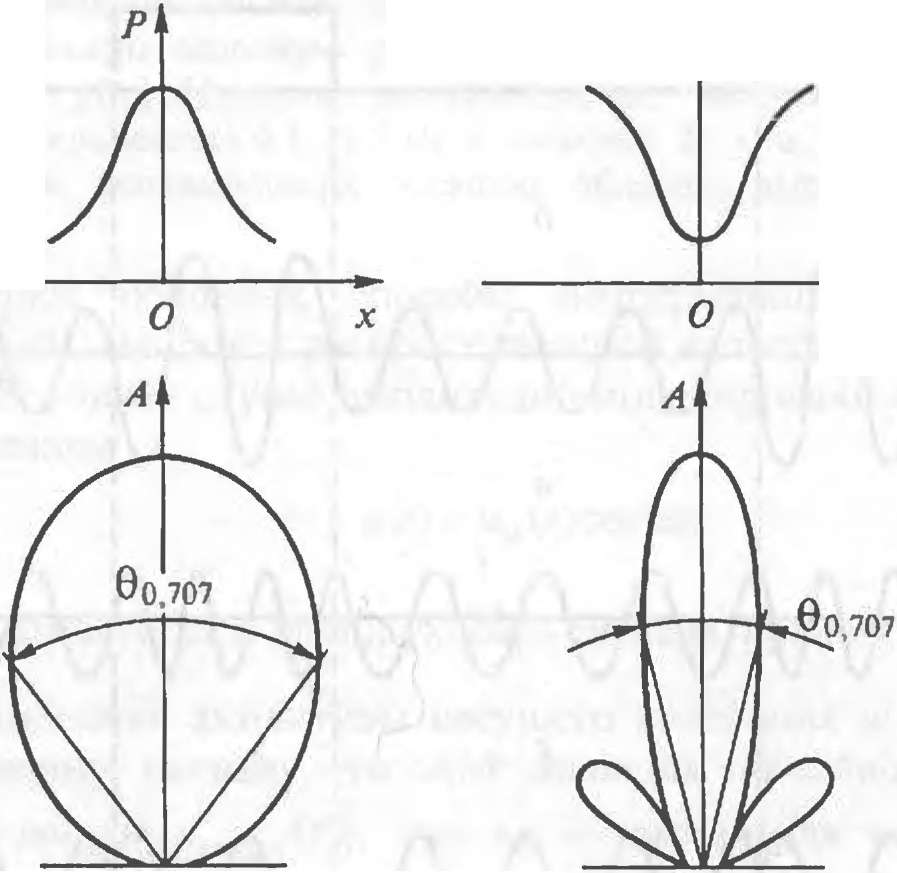
Зависимость вида диаграммы направленности от амплитудного распределения мощности

Модуляция и детектирование сигналов

Основным принципом передачи информации в ЛС является модуляция — изменение по заданному закону во времени некоторых параметров, характе­ризующих сигнал. Обычно такими параметрами являются его амплитуда, час­тота и фаза. Так как информация в ЛС переносится волновыми процессами, то имеет место модуляция колебаний, т. е. вариация какого-либо параметра периодических колебаний, медленная по сравнению с самими колебаниями. Колебание, с помощью которого передается сигнал, называется не­сущим, а его частота f— несущей частотой. Несущее колеба­ние имеет более высокую частоту, чем частота f_м переносимого (моду­лирующею) сигнала, которая называется модулирующей частотой. При описании модуляции обычно используют понятие круговой частоты ω=2πf. В дальнейшем для краткости со также будем называть не­сущей частотой, а ω_м — частотой модулирующею сигнала.

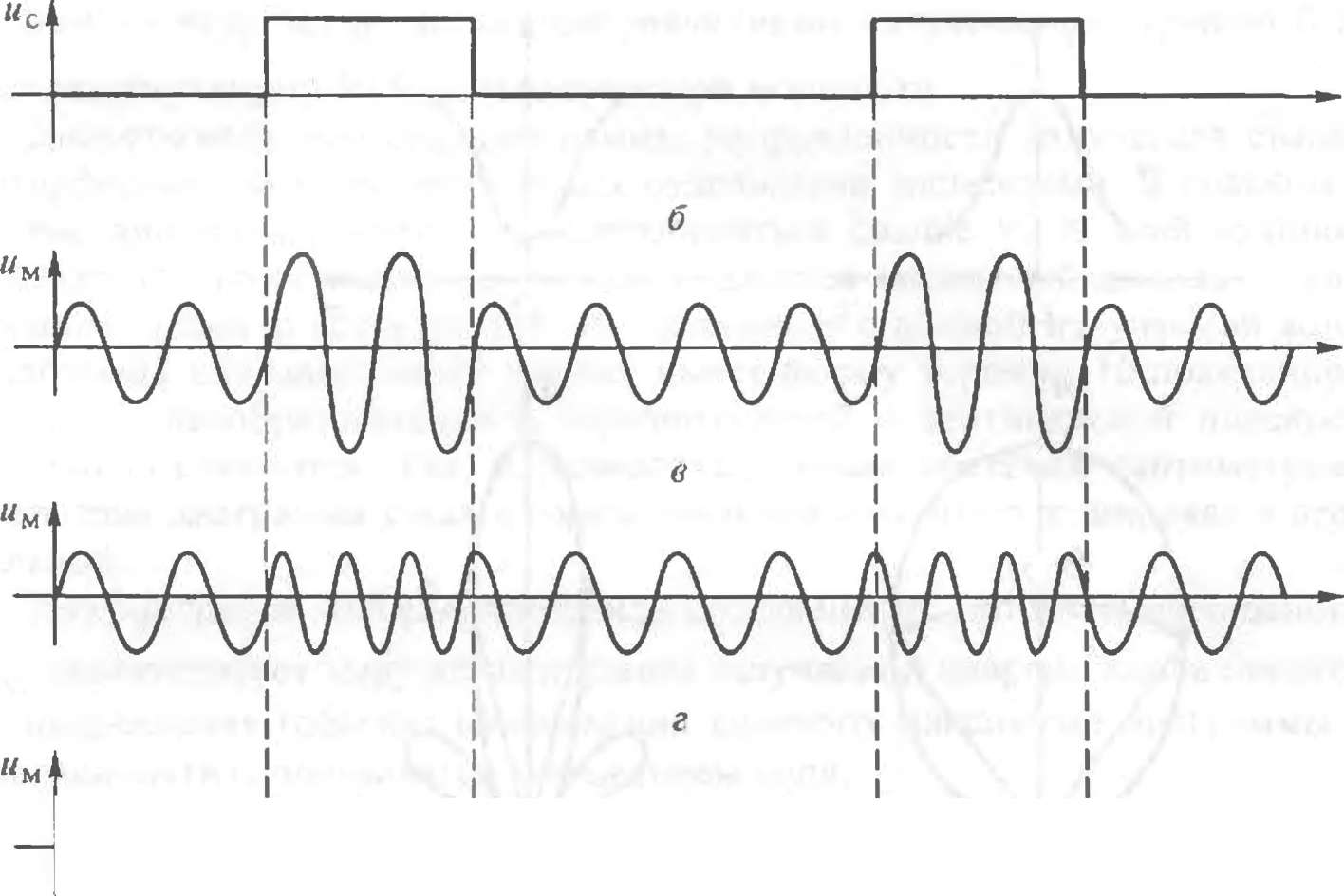
Модулированные колебания:

а — несущее колебание; б — модулирующий сигнал; в — б — амилитудно-, частотно- и фазово-модулированное колебание соответственно и разделяют непрерывную и импульсную модуляции. В первом случае мо­дулирующий сигнал изменяет амплитуду, частоту или фазу несущего коле­бания, во втором — кроме указанных имеет место также вариация ширины импульсов, а также импульсно-кодовая модуляция. При любом способе не­прерывной модуляции скорость изменения амплитуды, частоты или фазы должна быть достаточно мала, чтобы за один период несущего колебания Т = 1/f = 2π/ω модулирующий сигнал почти не менялся. Обычно круговую частоту несущего колебания (несущую частоту) выбирают из условия

ω >5ω_м . При импульсной модуляции вместо круговой частоты используют

термин частоты следования импульсов ω, которая в соответствии с теоре­мой Шеннона должна быть по крайней мере вдвое выше максимальной час­тоты модулирующего сигнала: ω_н >2ω_м .

Сложение сигналов с близкими частотами вызывает биение, которое можно рассматривать и как модуляцию.

В живой природе при локации используется как непрерывная, так и импульсная модуляция. Первая характерна для летучих мышей, вторая — для дельфинов и на­земных млекопитающих. В обоих случаях имеет место частотная модуляция, при­чем закон изменения частоты довольно сложен и определяется конкретной задачей. Так, летучая мышь в обычных условиях в течение 40 .. 100 мс излучает ультразвуко­вые сигналы постоянной частоты 70...80 кГц, но в конце подачи сигнала эта часто­та за 1...5 мс линейно убывает до 45...60 кГц. Локационные сигналы дельфинов имеют существенно меньшую длительность (0,04...0,1 мс), но более широкий спектр (30.,. 150 кГц). Наземные млекопитающие, например землеройки, излучают импульсы длительностью 0,1...3,5 мс и частотой 20 кГц. Слуховая (приемная) сис­тема животных, использующих локацию, обладает выраженными резонансными свойствами.

Рассмотрим основные способы непрерывной модуляции сигналов. Наиболее распространенной является амплитудная модуля­ция (АМ). В общем случае амплитудно-модулированный сигнал определя­ется выражением

u(t)=u_m(t)cosωt

где u_m — амплитуда модулирующего сигнала.

Если изменение амплитуды несущего колебания и u(t) пропорционально модулирующему сигналу, то АМ является линейной. В этом случае

U(t)=u₀(1+mu_m(t)/u_мmax(t)), где u₀— амплитуда несущего колебания, m — глубина модуляции, характеризующая степень изменения амплитуды:

M=(u_mmax – u_mmin )/(u_mmax +u_mmin )

0<m<1, u_mmax, u_mmin - максимальная и минимальная амплитуды модулирующего

сигнала соответственно.

В простейшем случае, когда модулирующий сигнал является гармониче­ским:

U(t)=u₀(1+mcosω_mt)cos(ωt+φ),

где φ — начальная фаза несущего колебания.

Для определения спектра амплитудно-модулированного сигнала вели­чиной φ можно пренебречь. Следовательно, при т = 1 мощность каждого спутника составляет лишь 25 % от мощности несущего колебания. Чем больше глубина модуляции, тем больше мощность, переносимая спутниками, т. е. лучше отношение сигнал/шум. Однако на практике т = 0,6...0,8, поскольку при т > 0,8 резко возрастают искажения при детектировании амплитудно-модулированного сигнала. Ширина спектра До при АМ определяется как разность между наибольшей (верхней) и наименьшей (нижней) частотами спектра и в рассматриваемом случае равна 2ω_м

Амплитудно-модулированный сигнал (а) и его спектр (б)

В общем случае модулирующий сигнал u_m(t) имеет более сложный

спектр: спутник состоит уже не из одночастотного сигнала, а из набора сиг­налов разных частот, образующих по обе стороны от несущей две полосы боковых частот. Если АМ линейная, то нижняя (левая) полоса боковых час­тот в точности повторяет форму модулирующего сигнала, а верхняя (пра­вая) является ее зеркальным отражением (см. пунктирные линии на рис. 5.5, б). Анализ спектра сигнала свидетельствует, что полезную инфор­мацию можно восстановить по любой боковой полосе. Для этого в схемах детектирования подавляют несущую частоту и одну из боковых.

Достоинством АМ является простота решений и малая ширина спектра сигнала, составляющая десятки килогерц при передаче звукового и десятки мегагерц при передаче телевизионного сигнала. В то же время передача ам­плитудно-модулированного сигнала требует значительных энергетических затрат, причем мощность полезного сигнала зависит от глубины модуляции. Так, при мощности несущего колебания 500 Вт мощность каждого спутника даже при т = 1 не превышает 125 Вт, а поскольку для уменьшения искаже­ний т < 0,8, следовательно, доля полезного сигнала еще меньше.

При частотной модуляции (ЧМ) модулирующий сигнал u_m(t) изменяет мгновенные значения частоты со, не влияя на амплитуду колебаний. Характерным примером является известный скрипичный прием виб­рато, когда качание пальца на струне изменяет ее длину и тем самым высоту звука. Чаще всего используют линейную ЧМ, при которой изменение несу­щей частоты пропорционально амплитуде модулирующего сигнала.

В простейшем случае модуляции гармоническим сигналом u_m(t)= u_mmax(t)cos_mt несущая частота со изменяется по закону

ω(t)=ω₀+Δ_ωcosω_mt

Здесь представляет собой амплитуду отклонения несущей частоты со от начальной ω₀, а cosω_mt определяет форму модулирующего сигнала. Пара­метр Δ_ω, называемый девиацией частоты, не зависит от частоты сигнала и соответствует глубине модуляции при АМ.

Ширина спектра Дсо частотно-модулированного сигнала определяется значением индекса ЧМ: β= Δ_ω / ω_{m .}При малых р ширина спектра практи­чески не зависит от его значения и равна 2 ω_m .В этом случае частотно-модулированный сигнал, как и амплитудно-модулированный, со­стоит из колебания с несущей частотой ω₀ и двух спутников с частотами ω₀ - ω_m и ω₀ + ω_m,

т. е. при малых β спектры амплитудно- и частотно-модулированных сигналов одинаковы. Однако, как правило, β»1, и, следовательно, спектр

частотно-модулированного сигнала значительно шире, чем амплитудно-модулированного.

В большинстве случаев модулирующий сигнал не является гармониче­ским, а представляет собой набор частот. Для примера рассмотрим передачу частотно-модулированных сигналов звукового диапазона 20 Гц ... 20 кГц на несущей частоте 50 МГц. Пусть при увеличении амплитуды модулирующе­го сигнала в диапазоне от 0 до 1 В несущая частота будет изменяться от 49,9

до 50,1 МГц, т. е. девиация частоты = 0,2 МГц. Для верхней частоты пе­редаваемого сигнала, равной 20 кГц, индекс Р = 10 и ширина спектра составит 440 кГц. (Для нижней частоты сигнала при тех же условиях р = 10 .) Поскольку (3 имеет различные значения при изменении частоты модули­рующего сигнала, в настоящее время принят стандарт, в соответствии с ко­торым индекс ЧМ вычисляют по формуле

β_max= Δ_ωmax / ω_mmax . Например, при передаче звука в телевизионном стандарте максимальная девиация несущей частоты звукового сопровождения Д(0тах = ^0 кГц, а

максимальная модулирующая частота сомпш = 15 кГц, при этом (Зтах = 3,33.

Амплитуда колебания несущей частоты при ЧМ в отличие от АМ зави­сит от амплитуды им модулирующего сигнала и при некоторых значениях индекса (3 обращается в нуль. Поскольку ширина спектра частотно-моду­лированного сигнала намного больше, чем амплитудно-модулированного, ЧМ используют в диапазоне метровых волн, соответствующем частотам от 50 МГц и выше.

Основным достоинством ЧМ является высокая помехоустойчивость. Обусловлено это главным образом тем, что амплитуда частотно- модулированного сигнала постоянна и, следовательно, аддитивные помехи на нее не влияют. Кроме того, вследствие постоянства амплитуды частотно- модулированного сигнала его мощность изменяется незначительно. Еще одним достоинством ЧМ является наличие дополнительных линий в спектре сигнала, что повышает надежность связи.

Фазовой модуляцией (ФМ) называется способ модуляции, при котором фаза колебания с несущей частотой изменяется в зависимости от амплитуды ым модулирующего сигнала. Модулированный сигнал при ФМ колебания с

несущей частотой ω₀ гармоническим сигналом / имеет вид

где — индекс ФМ, характеризующий максимальное отклонение фазы модулированного сигнала от фазы исходного.

Несущая частота при ФМ, как и при ЧМ, непостоянна и определяется со­гласно выражению

Девиация частоты при ФМ зависит от частоты модулирующего сигна­ла . Если модулирующий сигнал мм гармонический, то спектры фазово- и частотно-модулированного сигналов практически одинаковы.

В противном случае законы изменения фазы и частоты сигнала оказываются различными. Для ФМ с небольшим индексом спектр боковых частот прак­тически такой же, как и при АМ.

Проведенный обзор способов непрерывной модуляции позволяет сде­лать вывод, что качественное различие существует лишь между АМ, с одной стороны, и ЧМ или ФМ — с другой. Для всякого закона изменения частоты всегда может бьпь указан эквивалентный закон изменения фазы. В отличие от АМ глубина ЧМ и ФМ, характеризуемая соответственно индек­сами ( , не изменяет средней мощности модулированного сигнала, в то время как ширина спектра этого сигнала увеличивается с возрастанием глу­бины модуляции.

В ЛС наряду с непрерывной модуляцией широко применяют импульсную модуляцию (ИМ) сигналов. В этом случае переносчиком сигнала служит по­следовательность импульсов, каждый из которых обычно представляет со­бой цуг колебаний с высокой несущей частотой, Данная последовательность используется в схемах ИМ, где параметры импульсов модулируются сигна­лом. Частота посылок импульсов, называемая частотой дискретизации , определяется спектром передаваемого сигнала и должна по крайней мере в 2—3 раза превышать верхнюю частоту спектра модулирующего сигнала. В этом случае возможна демодуляция сигнала, т. е. выделение необходимой информации из импульсно-модулированного сигнала. Так, для разборчивого воспроизведения речевых сообщений достаточно передавать спектр частот 0,1 — 3 кГц, что требует обеспечения частоты дискретизации 8... 10 кГц. По сравнению с гармоническими колебаниями импульсы характеризуются большим числом параметров, поэтому видов ИМ значительно больше. Кро­ме амплитуды, частоты и фазы различают длительность (или ширину) им­пульсов т и их скважность Использование импульсов с большой

скважностью позволяет в рамках одного частотного канала (т. е. при одной и той же частоте дискретизации) сформировать несколько информационных каналов. Например, если в рассмотренном выше случае ограничить дли­тельность импульса значением 1 мке, т. е. при частоте дискретизации 10 кГц обеспечить скважность, равную 100, то можно сформировать несколько де­сятков каналов передачи речевых сообщений. Этот подход, получивший название временной селекции, характерен для многоканальных систем свя­зи. Обычно в ЛС применяют модуляцию импульсами прямоугольной или

колоколообразной формы с .

Наибольшее распространение получили амплитудно-, частотно-, широт- но- и фазово-импульсный, а также импульсно-кодовый способы модуляции сигналов.

Вид сигнала на выходе излучателя ЛС дан на рисунке. При фазово-импульсной модуляции импульсы, имеющие постоянную амплитуду и длительность, смещаются относительно некоторых фиксированных моментов времени в сторону опережения или отставания на временные интервалы, пропорциональные мгновенным зна­чениям передаваемого сигнала. Вид сигнала на входе приемника ЛС после прохождения через среду распространения показан на рис. 5.7, д, а тот же сигнал после фильтрации и детектироваиия — на рис. 5.7, е. Помехоустой­чивость ЛС возрастает при использовании фазово- и кодово-импульсной модуляции сигналов. Последняя приобретает особое значение в связи с ак­тивным развитием систем цифровой связи. К недостаткам ИМ по сравнению с непрерывной можно отнести большую ширину спектра сигнала и слож­ность технической реализации.

Для восстановления информации из модулированных сигналов приме­няют схемы демодуляции. Рассмотрим демодуляцию амплитудно-моду- лированного и частотно-модулированного сигналов В первом случае ис­пользуют методы амплитудного детектирования, во втором — частотной демодуляции.

Основными элементами амплитудного детектора (рис 5.8, а) являются

усилитель , диод и фильтр низкой частоты, построенный на основе

RC-контура. Эмиттерный повторитель служит для снижения выходного

сопротивления схемы. Подадим на вход усилителя амплитудно-мо­дулированный сигнал вида

,

где Uо — амплитуда напряжения модулирующего сигнала. Обозначая и полагая φ = 0, получаем

Если соотношение элементов фильтра удовлетворяет условию , то на выходе схемы имеем

где — динамическая чувствительность схемы

Постоянную составляющую детектируемого напряжения устраняем

с помощью фильтра верхних частот на конденсаторе С. Графическая иллю­страция работы детектора представлена на рис. 5.8, б.

Одной из схем частотной демодуляции является частотный дискримина­тор (детектор наклона), принцип работы которого основан на пропорцио­нальном изменении амплитуды напряжения на колебательном контуре с элементами R, L и С при вариациях мгновенных значений частоты модули­рованных колебаний.

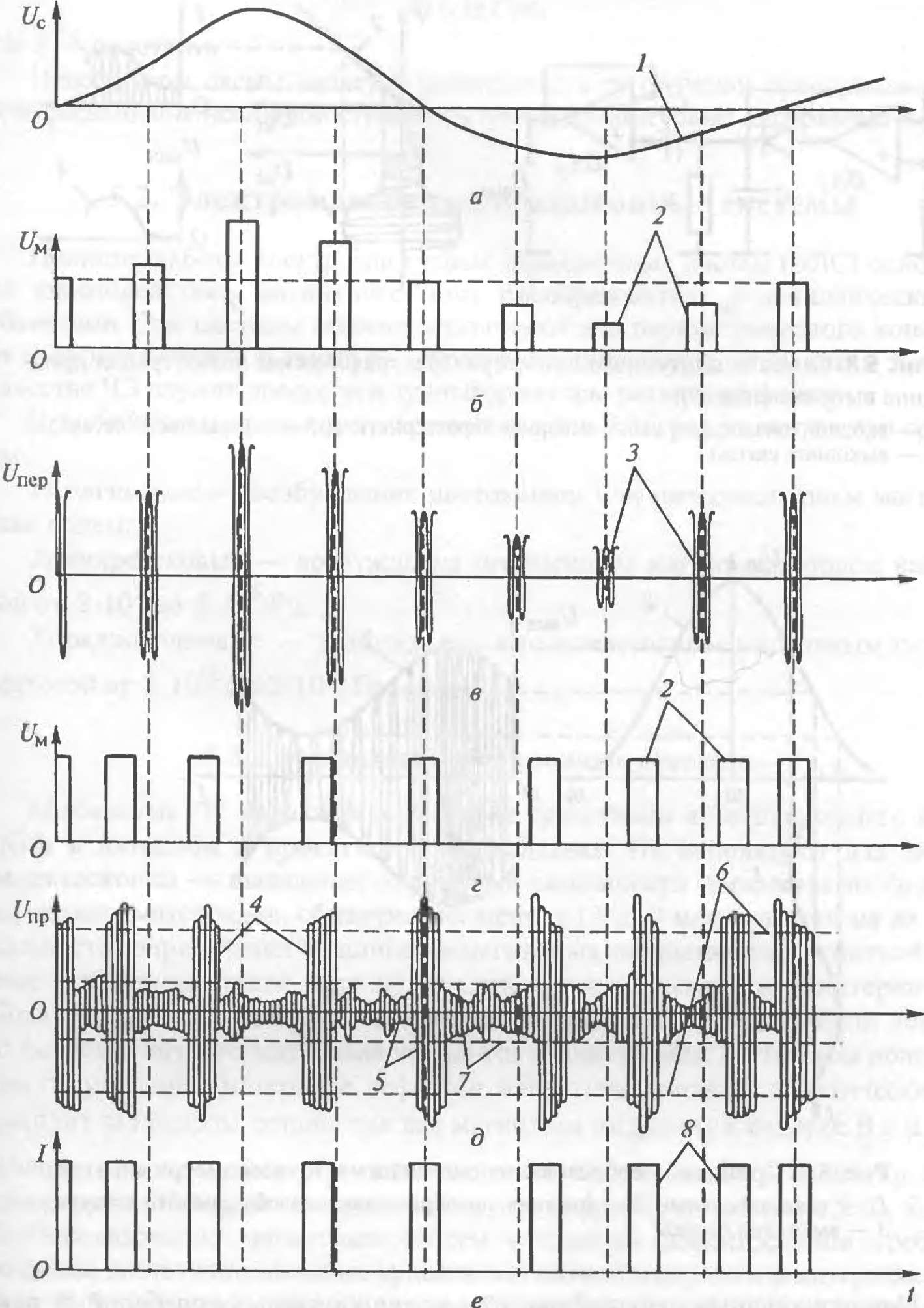
Примеры амнлитудно- (а—в) и фазово-импульсной (г—е) модуляции сигнала:

/ — модулирующий сигнал; 2 — модулированный сигнал, 3 — импульсы на выходе из­лучателя, 4 — импульсы на входе приемника; 5 — шум; 6,7 — верхний и нижний поро­ги ограничения амплитуды сигнала; 8 — импульсы после ограничения и фильтрации

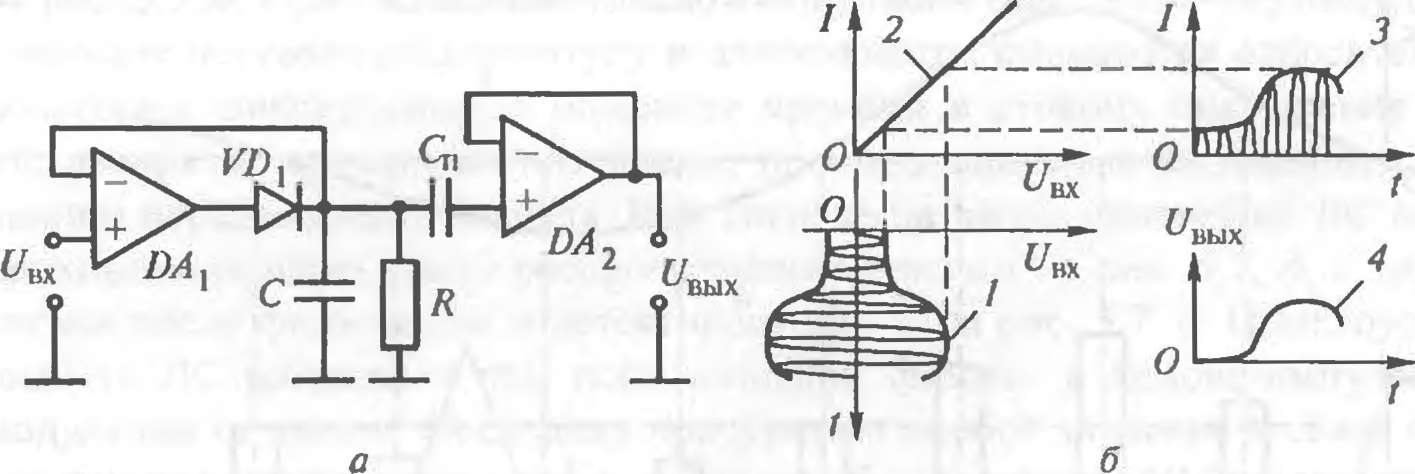
Схема амплитудного детектора (а) и графическая иллюстрация прин­ципа выпрямления (б):

/ — входной сигнал, 2 — вольг-амперная характеристика; 3 — сигнал после детектора; 4 — выходной сигнал

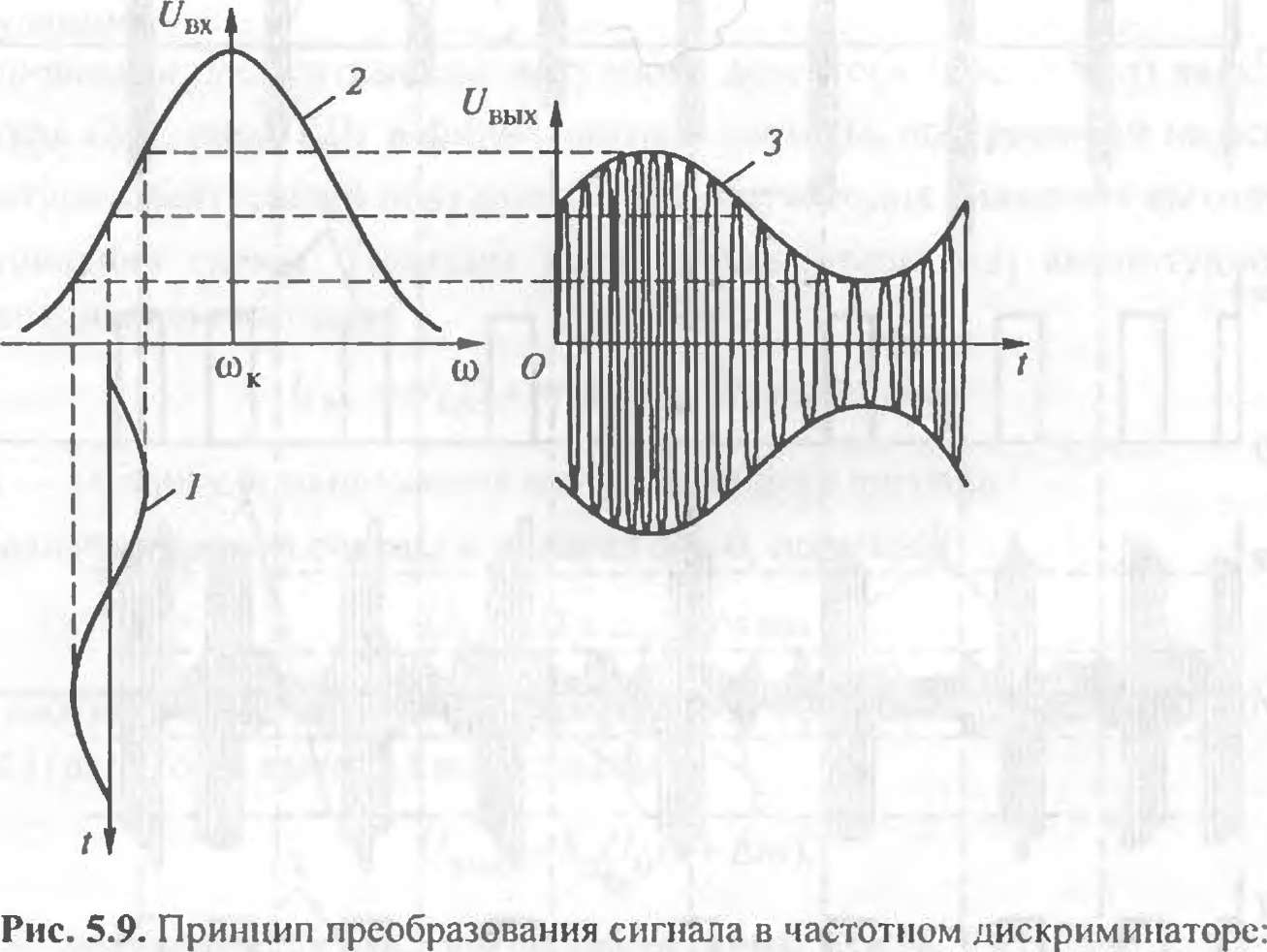
У — входной сигнал; 2 — функция преобразования колебательного контура; 3 — выходной сигнал

При отклонениях несущей частоты модулированных колебаний от резо­нансной частоты сок контура изменяется амплитуда выходного сигнала

С/ВЬ1Х, причем влияние модулированных колебаний тем слабее, чем острее резонансная кривая (рис. 5.9). Резонансные свойства контура зависят от его добротности 0, определяемой выражением

где к — константа.

Недостатком схемы является нелинейность ее функции преобразования. Для уменьшения нелинейности используют двухконтурные дискриминаторы.

5.2. Электромагнитные локационные системы

Принцип работы электромагнитных локационных систем (ЭЛС) основан на взаимодействии магнитного поля преобразователя с металлическими объектами. Эти системы обычно используют для параметрического контро­ля и дефектоскопии, а также для измерения расстояний, вибраций и т. п. В качестве ЧЭ служат дроссели и трансформаторы различной формы.

В зависимости от частоты магнитного поля ЭЛС разделяют на три груп­пы:

магнитные — возбуждение постоянным или низкочастотным магнит­ным полем;

вихретоковые — возбуждение переменным магнитным полем часто­той от 2 • 102 до 5 106Гц;

радиоволновые — возбуждение высокочастотным магнитным нолем

частотой от .

5.2.1. Магнитные локационные системы

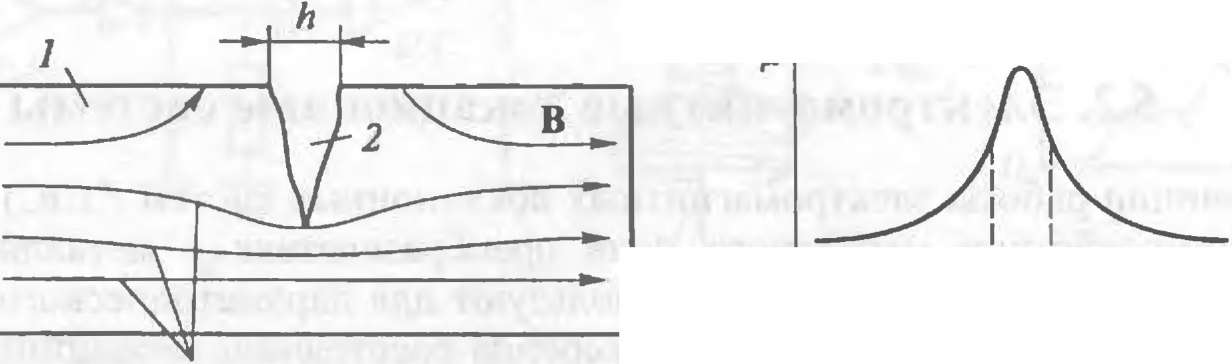
Магнитные ЛС являются основными средствами неразрушающего кон­троля в литейном и прокатном производствах. Их используют для задач дефектоскопии — выявления нарушений сплошности предметов из ферро­магнитных материалов, обнаружения мелких (3...10 мкм) трещин на их по­верхности, определения толщины немагнитных покрытий на магнитной ос­нове и толщины стенок изделий из магнитных и немагнитных материалов. Принцип магнитной дефектоскопии иллюстрирует рис. 5.10, а. Если деталь из ферромагнитного материала находится в однородном магнитном поле, то при отсутствии в материале дефектов магнитный поток Ф практически не выходит за пределы детали, так как магнитная индукция в воздухе В в р. раз

меньше, чем в металле. Следовательно, магнитное сопротивление тре­щины шириной к будет намного выше, чем ферромагнетика (рис. 5.10, б).

Использование магнитных систем в задачах дефектоскопии требует создания достаточно высоких уровней магнитной индукции в материале де­тали. Поэтому определяющее значение приобретают собствешю магнитные характеристики материала, для оценки которых используют такие парамет­ры, как остаточная индукция #осх, намагниченность Е и магнитная воспри­имчивость <;. Намагниченность представляет собой векторную величину, характеризующую состояние материала при воздействии на него магнитно­го поля напряженностью Н:

где Мц — магнитный момент единицы объема V тела.

Рис. 5.10. Распределение магнитного поля (а) и изменение магнитного сопротивления (б) в области дефекта: 1 — деталь; 2 — трещина; 3 — магнитные линии

Индукцию в намагниченном материале определяют ио формуле

В =

Магнитная восприимчивость ζ характе­ризует способность материала намагничиваться в магнитном поле и ζ= . Для всех металлов ζ зависит от магнитной проницаемости

при­чем для диамагнетиков , а для парамагнетиков . Поскольку в обоих случаях |1 не зависит от напряженности магнитного поля и мало отличается от единицы, значения магнитной восприимчивости для диа- и парамагнетиков весьма малы: соответственно. Магнитные де­фектоскопы позволяют обнаруживать подповерхностные трещины и ра­ковины на глубине до 20 мм.

Магнитные ЛС применяют также для измерения зазоров в магнитных цепях. В системах этого типа используют как индуктивные, так и индукци­онные датчики. В первых вариация магнитного сопротивления зазора вызы­вает изменение индуктивности катушки, во вторых — ЭДС индукции. В простейших магнитных системах катушка внешним источником питания не возбуждается; при этом выходной сигнал возникает только при движении объекта относительно датчика. На этом принципе построены магнитные го­ловки разных типов, использующиеся в системах магнитной записи сигна­лов. Для повышения эффективности магнитных головок их сердечник вы­полняют из материала с большой магнитной проницаемостью (феррита, пермаллоя и др.). В системах измерения зазоров или малых расстояний го­ловка содержит две катушки — первичную и вторичную, при этом первая является катушкой возбуждения и питается от внешнего источника напря­жения, а вторая — сигнальной.

Пример использования индукционной головки наведения для управле­ния подвижным мобильным средством приведен на рис. 5.11, а. Головка включена в состав навигационной системы транспортной тележки, переме­щающейся внутри цеха вдоль уложенных под полом металлических шин. Катушка возбуждения создает высокочастотное электромагнитное поле, ко­торое на поверхности металлической шины наводит соответствующее маг­нитное поле, под действием которого во вторичных (сигнальных) катушках генерируются переменные напряжения. Обмотки катушек соединены диф­ференциально, в результате чего их суммарный сигнал ( соответствует разности напряжений в каждой катушке. Угловое рассогласование а вы­зывает на выходе фазочувствителыюго выпрямителя сигнал , ам­плитуда которого пропорциональна напряжению , а знак соответствует

фазе а (рис. 5.11, б). В некоторой зоне измерения при < ±40° достига­ется линейность функции преобразования головки наведения

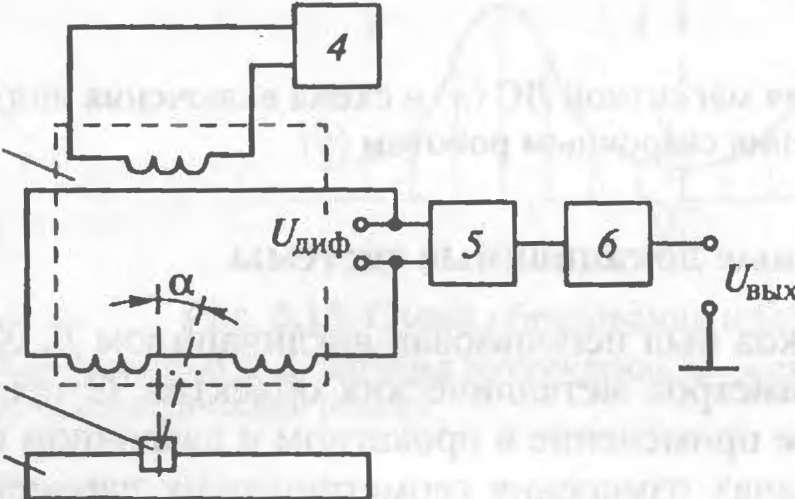
. Схема индукционной головки наведения (а) и се функция преобразова­ния (б):

1 — поверхность пола, 2 — металлическая шина, 3 —датчик, 4 — генератор; 5 — прием­ник, 6 — фазочувст витсльный выпрямитель

В робототехнике магнитные ЛС с индуктивными датчиками широко ис­пользуют для определения расстояния до металлического объекта. На рис 5.12 представлена функция преобразования и схема включения индуктив­ного датчика в контур управления сварочным роботом. Выходные сигналы поступают в регулятор привода, который перемещает исполнительный орган (сварочную головку) по соответствующей оси до тех пор, пока не будет до­стигнуто требуемое расстояние /раб между электродом и поверхностью за­готовки. Это расстояние, определяемое эмпирически, составляет в среднем 6; 4 и 3 мм для черных металлов, алюминия и меди соответственно. Погрешность позиционирования головки при отслеживании траектории равна ± 0,4 мм.

К достоинствам магнитных ЛС можно отнести простоту конструкций, большую глубину зоны контроля, высокую надежность (на показания дат­чика практически не влияют климатические факторы и загрязнение поверх­ности), к недостаткам — низкую разрешающую способность и нелиней­ность функции преобразования

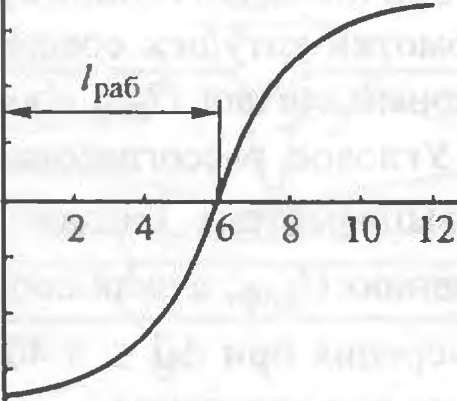
Функция преобразования магнитной ЛС (а) и схема включения индук­тивного датчика в контур управления сварочным роботом (б)

Вихретоковые локационные системы

Впервые датчик вихревых токов был использован англичанином Д. Хыо- зом в 1879 г. для сравнения параметров металлических объектов. С тех пор вихретоковые ЛС нашли широкое применение в прокатном и сварочном про­изводствах, на транспорте, в задачах измерения геометрических параметров быстропротекающих процессов движения и др. Системы этого типа работают в условиях активного воздействия внешней среды (при значительных перепа­дах температур и влажности, в агрессивных средах и т. д.).

Работа вихретоковой ЛС основана на взаимодействии внешнего магнит­ного поля с электромагнитным полем вихревых (замкнутых) токов, наводи­мых возбуждающей катушкой в любом электропроводящем объекте1. Си­нусоидальный или импульсный ток, действующий в катушке возбуждения датчика, создает электромагнитное поле, которое вызывает вихревые токи в материале объекта. Электромагнитное поле этих токов воздействует на сиг­нальную катушку, наводя в ней ЭДС. В простейших схемах (без сигнальной катушки) вихревые токи воздействуют непосредственно на катушку возбуж­дения. Сила / вихревых токов, возбужденных в изделии, определяется урав­нением Максвелла и зависит от частоты тока обмотки возбуждения, материала объекта (его удельного электросопротивления р и магнит­ной проницаемости μ), а также расстояний между катушками и объектом. Принцип формирования вихревых токов в материале был открыт в 1825 г Д. Араго и развит впоследствии его учеником Л. Фуко.

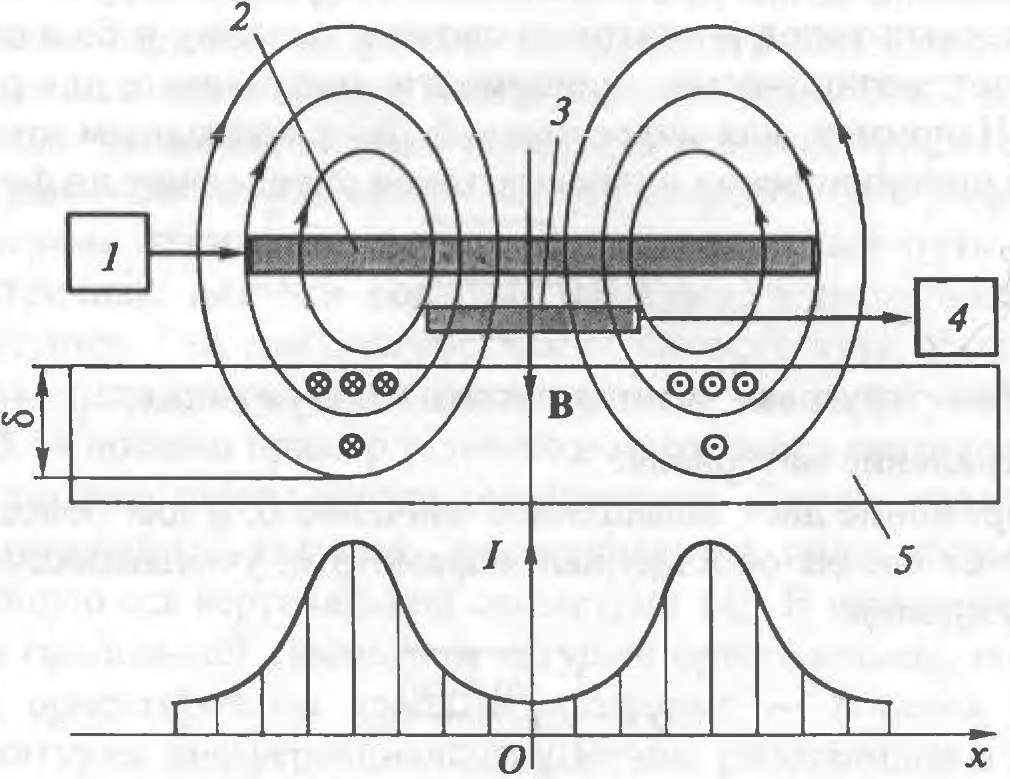
Схема образования и эпюра вихревых токов

контроля, что требует устранения постоянной составляющей, обусловленной ка­тушкой возбуждения. При ортогональном же расположении катушек ток в сигнальной катушке наводится только вихревыми токами, однако и уровень выходного сигнала при этом будет ниже, чем в первом и втором случаях.

Расчет вихревых токов достаточно сложен, поэтому в большинстве слу­чаев используют эмпирические зависимости, полученные для разных част­ных случаев. Например, для вихретоковой ЛС с накладным преобразовате­лем глубину 8 проникновения вихревых токов определяют по формуле

где круговая частота тока возбуждения; р — удельное

электросопротивление материала.

Данное выражение дает завышенное значение 5, и для более точных из­мерений в расчет вводят обобщенный параметр учитывающий диаметр (I катушки возбуждения:

Следовательно,

Значение δ глубины проникновения вихревых токов тем ближе к реаль­ному, чем больше параметр г), например диаметр катушки возбуждения. При работе в диапазоне частот 0,1... 10 кГц для большинства металлов 5 < 0,5...5 мм и уменьшается с увеличением частоты.

В дефектоскопии с помощью вихревых токов удается обнаружить тре­щины наружного и внутреннего зале1ания длиной 1...2 мм и глубиной 0,1...0,3 мм, раковины с глубиной залегания до 6 мм, неметаллические включения. Вихретоковые ЛС позволяют измерять толщину покрытий в диапазоне 0,001.. 1,0 мм. Для увеличения глубины проникновения вихревых токов применяют специальные меры. Например, создавая в материале маг­нитное насыщение (уменьшая его магнитную проницаемость), увеличивают глубину проникновения вихревых токов до 10 мм.

Особенностью вихретоковых ЛС является их многопараметричность, так как ЭДС преобразователя зависит от разных характеристик объекта контроля и окружающей среды, неявно влияющих на выходной сигнал. Это обстоятельст­во определяет как достоинства, так и недостатки таких систем. Существенным недостатком всех многокомпонентных вихретоковых датчиков является высо­кий коэффициент влияния информационных каналов (Л'у ~ 12. .20 %). Для

компенсации интегрального влияния внешних факторов, вызывающих допол­нительную погрешность системы, в ее состав включают компенсационную катушку, на которую действуют те же факторы, что и на рабочие катушки, кроме непосредственно измеряемого параметра. Суммируя сигналы с катушек с помощью дифференциального усилителя (см. 2.3) можно существенно уменьшить дополнительную погрешность.

В задачах многопараметрического контроля, когда приходится измерять сразу несколько параметров, удобно использовать многокомпонентные вих- ретоковые датчики, получившие название матричных. ЭЛС, построенные на базе матричных датчиков, широко используют для контроля геометрических параметров движущихся узкопрофильных поверхностей с разрывами и усту­пами. Примерами таких объектов являются рельсовый путь и контактный провод. Матричные датчики содержат не одну, а несколько (матриц) си­гнальных катушек. Так, для диагностики рельсового пути обычно применяют четыре-шесть, а для контроля состояния провода — две катушки.

На рис. 5.14 показан пример установки матричного вихретокового датчика накладного топа на шасси вагона-дефектоскопа. Датчик представляет собой несколько идентичных катушек, намотанных на прямоугольный каркас и имеющих общую ось вертикальной симметрии Ог. В горизонтальной плоско­сти хОу оси продольной симметрии катушек ортогональны, поэтому некото­рые из них ориентированы вдоль, а некоторые — поперек рельса. Схема включения катушек дифференциальная. Датчик, работающий в диапазоне час­тот 0,1... 1,0 МГц, располагают непосредственно под вагоном на фиксирован­ном расстоянии над контролируемым рельсом. На рис. 5.14, а контролируемые параметры пути обозначены так: Ах, АН — смещение оси рельса в боковом и вертикальном направлении соответственно; Дг, Ду — изменение высоты и за­зор в стыке рельсов. На рис. 5.14, б показан боковой износ рельса Аг.

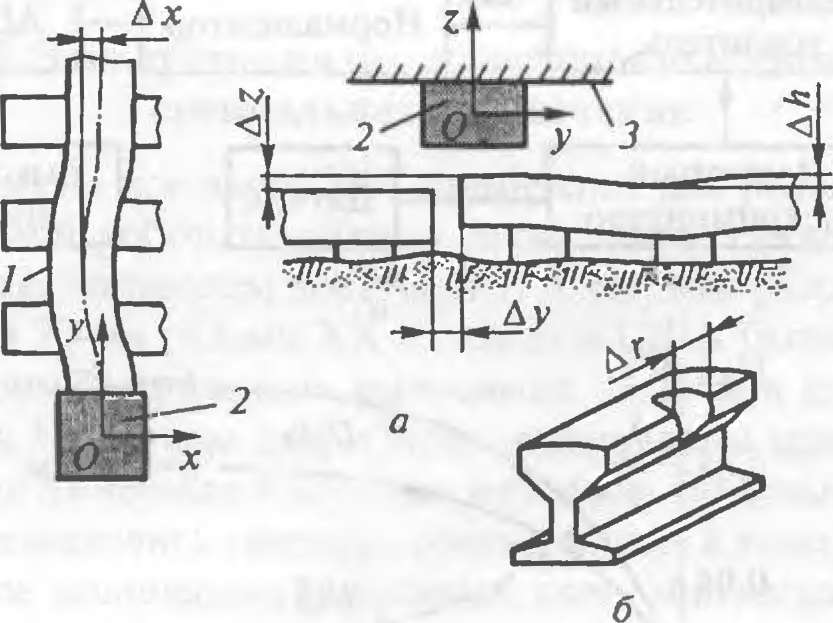
Схема установки матричного вихретокового датчика «Спектр» (с) и боковой износ рельса (б): / — рельсовая колея; 2 — датчик; 3 — вагон-дефектоскоп

В матричных датчиках осуществляется разделение измеряемых факторов. Например, кагушки, у которых в плоскости хОу оси продольной симметрии перпендикулярны оси рельса, наиболее чувствительны к изменению парамет­ров Дг, Ду и АН, а катушки, у которых эти оси параллельны оси рельса — к па- раметрам Ах и Аг. Рассмотренная система установлена в передвижной лабора­тории комплексной диагностики пути, способной проводить контроль при скорости движения вагона по железнодорожной магистрали до 80 км/ч

Другой распространенной областью применения вихретоковых ЛС явля­ется сварочное производство, где их используют для слежения за сварочным швом. Многокомпонентный вихретоковый датчик измеряет параметры вза­имного положения свариваемых деталей и сварочной головки: расстояние от центра датчика до объектов сварки или линии шва, ширину шва и др.

Важной областью применения вихретоковых ЛС является также нераз- рушающий контроль изделий металлургической промышленности. По­скольку структурное состояние металлов влияет на их электрические и магнитные свойства, оказывается возможным контролировать не только сплошность материала, но и его химический состав, а также качество тер­мической обработки и состояние поверхностного слоя после механической обработки. Схема такой системы для автоматизации процесса контроля сплошности отливок и се функции преобразования представлены на рис. 5.15. Система включает несколько разнотипных вихретоковых датчи­ков, что позволяет детерминировать различные дефекты: длину I и толщину И наружных царапин, глубину 6 залегания трещин и т. д. Выходным сигна­лом датчика является изменяющаяся частота генерации, которая с помощью частотного дискриминатора преобразуется в аналоговый амплитудный сиг­нал Цпых, пропорциональный измеряемому параметру. Заметим, что функ­ции преобразования данной системы нелинейны (см. рис. 5.15, б). Для их линеаризации в схеме используется нормализатор.

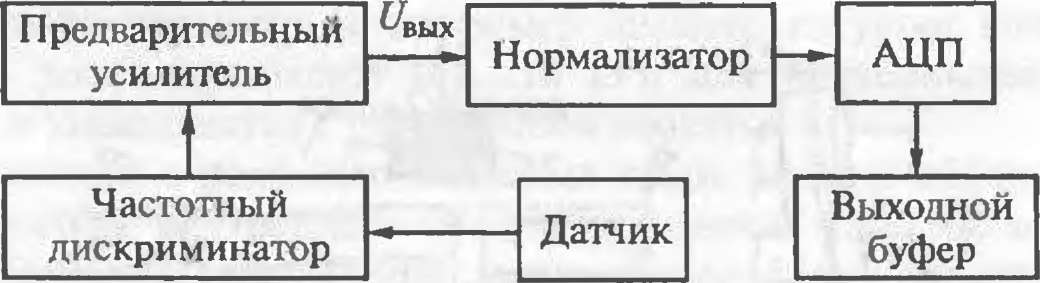
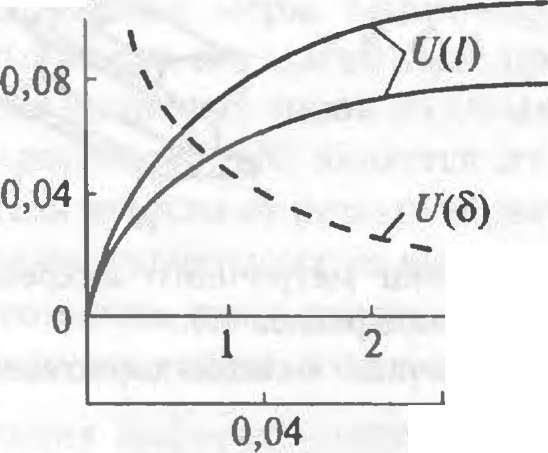
Схема вихретоковой системы для контроля качества отливок (а) и ее функции преобразования (б)

Модель	Измеряемый параметр	Диапазон измерений	е, %	/в, кГц	Р, Вт	Размеры, мм				т, кг
						а	/	Ь	И
дсм-	Глубина	2 мм	5	1000	10	—	230	270	150	2,7
0,1/1	залегания
(Россия)	трещины
ВМ-10Н	Шерохова­	0,3 мм	3	100	0,1	—	160	110	50	0,5
(Россия)	тость
	поверхности
	Вибрации	0,02...20 Гц	2	100	»	-	160	110	50	0.5
Т(} -403	Расстояние	1... 13 мм	5	20	Н.д.	20	65		„	0.25
(Швейца	до
рия)	объекта
МТП-01	Толщина	0,2... 10 мм	5	Н.д.	0,4	—	220	130	150	1,5
(Россия)	покрытия

Основные параметры вихретоковых ЛС

К достоинствам вихретоковых ЛС можно отнести надежность, простоту конструкций и высокую разрешающую способность; к недостаткам — не­линейность функции преобразования, низкую точность измерений, сравни­тельно малую глубину зоны контроля.