Выборочное среднее квадратическое отклонение равно

0,158442

Вычислим исправленную выборочную дисперсию

S ² = 0,02562 ;

Вычислим исправленное выборочное среднее квадратическое отклонение:

0,160. Обозначим результат S _x = 0,16 .

Полученные результаты позволяют сделать следующие выводы.

Средняя мощность пласта по выборке равна 1,14 м. Средний разброс мощности пласта вокруг среднего по выборке равен 0,16 м.

Аналогично определяем числовые характеристики выборки по признаку У. Выберем условный нуль С = 8,38 ; h = 1,48.

Таблица 8.

i	интервалы	уi	ni	ui	ni ui	ni ui2	ni (ui + 1)2
1	3,2 - 4,68	3,94	5	-3	-15	45	20
2	4,68 - 6,16	5,42	12	-2	-24	48	12
3	6,16 - 7,64	6,9	14	-1	-14	14	0
4	7,64 - 9,12	8,38	10	0	0	0	10
5	9,12 - 10,6	9,86	4	1	4	4	16
6	10,6 -12,08	11,34	3	2	6	12	27
7	12,08 -13,56	12,82	2	3	6	18	32
итого			50		-37	141	117

n_i(u_i+1)² = 117; n_iu_i² = 141; n_iu_i = –37, n = 50

117 = 141 + 2·(–37) + 50 – верно.

Из таблицы находим условные моменты:

М₁ = -37/50 = –0,74; М₂ = 141/50 = 2,82.

Выборочная средняя равна:

=М₁·h +C = –0,741,48+8,38= 7,2848.

Выборочная дисперсия равна:

D_в = [M₂ - (M₁)²]·h² = [2,82 – (-0,74²]·1,48² = 4,97746.

Выборочное среднее квадратическое отклонение равно

2,23102 .

S ² = 5,07905 ;

2,25367 .

Обозначим результат S _у = 2,25367 .

Полученные результаты позволяют сделать следующие выводы.

Средняя производительность труда рабочего очистного забоя для струговых установок на антрацитовых шахтах по выборке равна 7,28 тонны за выход. Средний разброс производительности труда рабочего очистного забоя для струговых установок на антрацитовых шахтах вокруг среднего по выборке равен 2,25 тонны за выход.

3 Интервальные оценки параметров распределения

Интервальной называют оценку, которая задается интервалом, покрывающим оцениваемый параметр генеральной совокупности. Доверительным называется интервал (,), который с заданной вероятностью  покрывает оцениваемый параметр генеральной совокупности. Вероятность  попадания оцениваемого параметра в доверительный интервал (,) называется доверительной вероятностью.

3.1 Доверительные интервалы для некоторых параметров распределения

Доверительный интервал для оценки математического ожидания a нормально распределенного количественного признака Х при известном среднем квадратическом отклонении  генеральной совокупности задается формулой:

, (1)

где  = 2Ф(t) – доверительная вероятность; – точность оценки.

Данная формула применяется для оценки математического ожидания М(Х) = а в двух случаях:

• если известно СКО – (х)=;

• если СКО неизвестно, но объем выборки достаточно велик (n > 30). В этом случае в качестве  берут ее оценку S.

Доверительный интервал для оценки математического ожидания a нормально распределенного количественного признака Х при известном среднем квадратическом отклонении  генеральной совокупности задается формулой:

, (2)

где t_ = t(,n) –находят по таблице приложения 3; – точность оценки.

Доверительный интервал для оценки среднего квадратического отклонения  нормально распределенного количественного признака Х задается формулой:

P{S(1 – q) <  <S(1+q)} =  , при q < 1 (3)

P{0 <  <S(1+q)} =  , при q > 1 . (4)

Здесь исправленное выборочное среднее квадратическое отклонение S служит оценкой для генерального среднего квадратического отклонения  ;

q=q(,n) – находят по таблице приложения 4;

n – объем выборки;  – доверительная вероятность;

 = qS – точность оценки.

Доверительный интервал для оценки неизвестной вероятности p биноминального распределения по относительной частоте  (выборочной доле) имеет вид

P{p₁ < p < p₂} =  , (5)

где р = Р(А) – неизвестная вероятность события А;

а концы интервала p₁ и p₂ определяются следующим образом:

а) Общий случай:

(6)

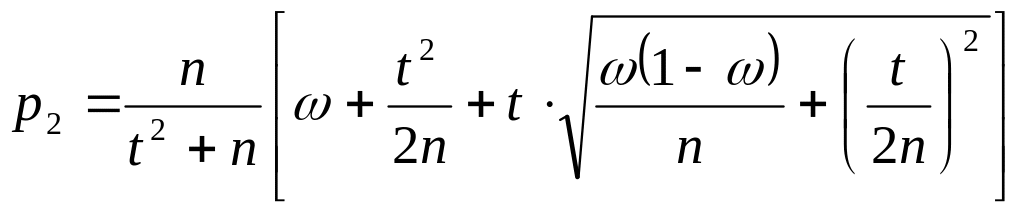
где n – объем выборки,  – доверительная вероятность;

t – находится из условия 2Ф(t) = ;

выборочная доля  находится по формуле = m/n, где n – общее число испытаний; m – число испытаний, в которых появилось событие А.

b) Частный случай – n велико (порядка сотен):

, (7)

с) Частный случай – известен объем генеральной совокупности N и n – велико:

,

(8)