1.1 Проверка данных

Очень важно, чтобы данные, полученные при статистическом анализе, были тщательно проверены и отредактированы до начала более сложного анализа. Никогда не следует забывать пословицу статистиков: «Мусор на входе – мусор на выходе».

Проверка данных может осуществляться на многих этапах статистических исследований:

• по корреляционному полю до первичной обработки данных при двумерном статистическом анализе;

• по статистическому ряду при одномерном анализе;

• по закону распределения при одномерном анализе.

Для проверки по корреляционному полю случайных величин Х и У, не разбитых на дискретные категории, необходимо построить точки в прямоугольной системе координат (х₁ ;y₁), (х₂ ;y₂), ..., (х_i ;y_i), …, (х_n ;y_n) . Полученное поле точек (диаграмма рассеяния) позволяет определить грубые ошибки и выбросы, не замеченные одномерным анализом каждой из переменных.

Для примера приведем корреляционное поле, где отмечены две точки, которые явно являются ошибочными.

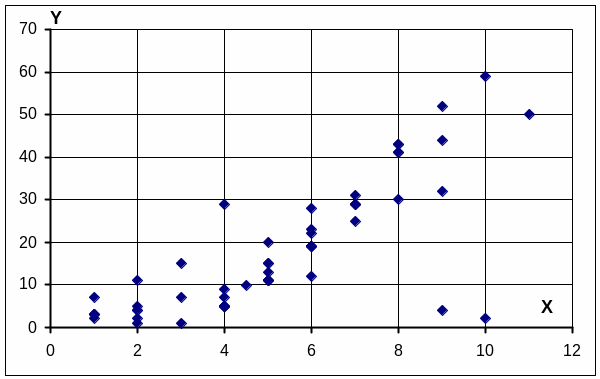
выбросы

В случаях выявления подобных точек не следует автоматически исключать их из выборки. Сначала надо проанализировать ситуацию, выявить возможные пути ошибок в каждом конкретном случае, а затем принимать решение по исключению данных из выборки. Если таких точек будет много, то, возможно, их надо выделить в отдельную группу.

В некоторых случаях с помощью корреляционного поля можно выявить не только аномальности в числовых данных, но и установить некоторые закономерности.

Возьмем такой пример. Пусть требуется установить, как мощность разрабатываемого пласта влияет на суточную участковую добычу угля. Была взята простая случайная бесповторная выборка по ряду показателей из нескольких шахт. Построено корреляционное поле.

В

Н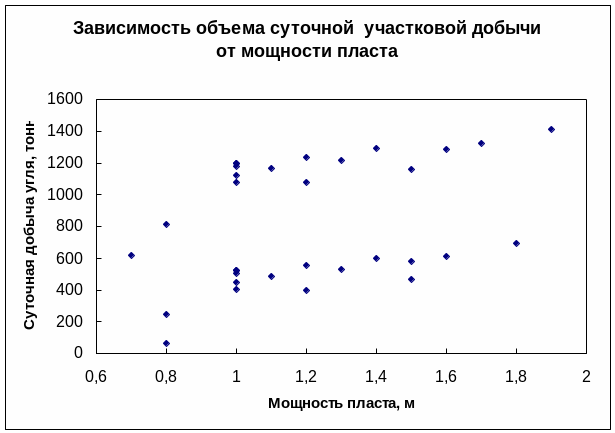

Из данной диаграммы видно, что множество точек корреляционного поля четко распадается на два подмножества (верхнее В и нижнее Н). Последующий анализ данных с учетом других, в том числе и качественных признаков, выявил, что множество Н соответствует выбросоопасным пластам угля, а множество В – не выбросоопасным пластам. Поэтому, на данном этапе исследования целесообразно проводить обработку статистических данных отдельно для выбросоопасных и не выбросоопасных пластов.

1.2 Группировка статистических данных

Первичная обработка статистических данных позволяет получить из исходного материала путем группировки статистический ряд (точечный или интервальный), а также эмпирическую плотность распределения и эмпирическую функцию распределения признака Х. Основные этапы первичной обработки:

а) определение минимального (х_min) и максимального (х_mах) элементов выборки;

б) определение рационального числа интервалов разбиения. Здесь нужно использовать формулу Стэрджесса:

k = 1 + 3,322 lg n при n <100;

k  10 при n  100.

в) определение шага интервала h = (х_max – х_min) / k

*допускается округлять в удобную для пользователя сторону.

г) подсчет числа частот n_i (можно при помощи штриховой отметки);

д) заполнение таблицы. Шаблон таблицы приводится ниже.

№	Интервалы	Штриховая отметка	Частота ni	Середина интервала хi	Частости wi	Ордината гистограммы	Накопленные частоты	Ордината кумуляты
1
2
…
			S1		S2	S3

Частости вычисляются по формуле: w_i= n_i/n.

Гистограмма характеризует эмпирическую плотность распределения, и ординаты ее точек определяются по формуле: y_i= w_i/h. Также по этим точкам строят полигон относительных частот. Если плотность распределения генеральной совокупности является достаточно гладкой функцией, то полигон относительных частот является более хорошим приближением плотности, чем гистограмма.

Накопленные частоты для каждого i –го интервала находятся как суммы частот n_i , начиная с первого интервала по i –ый.

Кумулята является графиком эмпирической функции распределения и ее ординаты равны накопленным частотам, деленным на объем выборки n.

Последняя строка таблицы  содержит суммы элементов некоторых столбцов и используется для контроля. При правильном заполнении таблицы должны выполняться следующие равенства:

S1 = n ; S2 = 1 ; S3h =1 .

Заполненная таблица позволяет записать статистический ряд (точечный или интервальный), а также построить гистограмму, кумуляту и полигон для данного распределения.