6. Реализация статистических расчетов при помощи компьютера

Современные компьютеры предоставляют большие возможности для расчета статистических характеристик. Отметим наиболее приемлемые компьютерные программы и способы обработки данных в них.

6.1 Табличный процессор Microsoft Excel

а) Почти ручной счет. Используя простейшие средства ввода, редактирования данных в данной программе на основании приемов и формул, представленные в разделах 1-5 настоящего пособия, можно проводить статистические расчеты в любом объеме. Этот способ хорош тем, что он позволяет пользователю создавать при помощи компьютера свой сценарий обработки данных и дает возможность просматривать, контролировать и активно влиять на промежуточные и окончательные результаты на всех этапах решения поставленных задач. Особенно удобно представлена в этом компьютерном приложении работа с таблицами и графиками, которые, как убедился читатель, являются неотъемлемыми атрибутами статистических расчетов. Примеры использования компьютера представленным способом приводится в разделах 1, 2 и 5. Недостаток этого метода связан с его достоинствами и заключается в относительно небольшой скорости расчетов и в необходимости знать все расчетные формулы (!!!).

б). Расчет статистических характеристик при помощи встроенных функций. В табличном процессоре Excel в меню Вставка имеется опция “Вставка функции” (кнопка f_х ). При выборе этой опции появляется диалоговое окно, разделенное на две части.

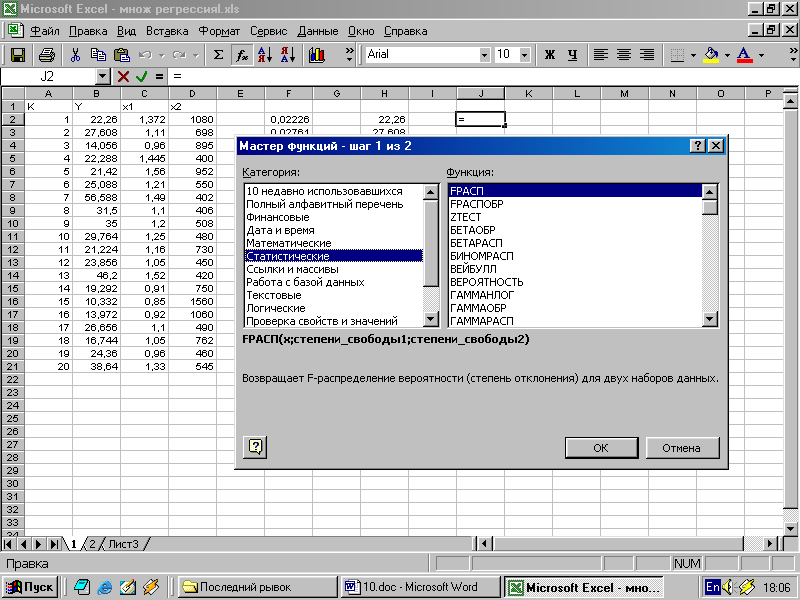
В левой части диалогового окна указываются категории функций. В нашем случае обычно выбирают категории Статистические и 10 недавно использовавшихся. В правой части диалогового окна выводится список функций данной категории. Если отметить какую-то функцию в этом списке, то в нижней части окна появится формула обращения к отмеченной функции, а еще ниже приводится краткое объяснение функции на русском языке. Если выбрать нужную функцию, то откроется соответствующее диалоговое окно. Для примера, выберем функцию КОРРЕЛ, которая позволяет вычислить коэффициент корреляции двух массивов (в нашем примере признаки Х и У):

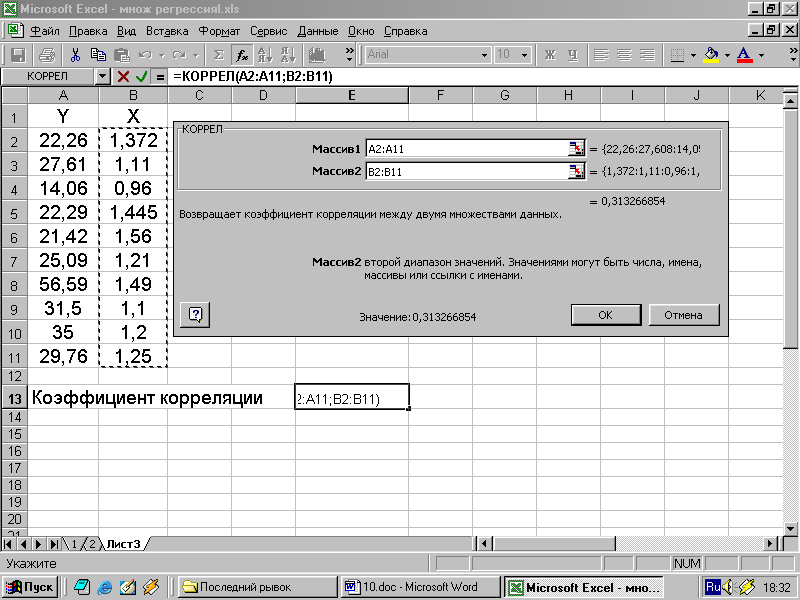
В появившемся окне нужно ввести запрашиваемую информацию. После нажатия кнопки ОК результат вычисления записывается в ту ячейку, которая была выделена пользователем до обращения к нужной функции.

Замечание. Если результат выполнения функции ожидается в виде массива, то вместо кнопки ОК нужно одновременно нажать три клавиши

Ctrl+Shift+Enter .

Перечислим некоторые наиболее используемые в данном пособии функции

Название функции в статистическом анализе	Обозначение в пособии	Обращение в Excel
Выборочное среднее		СРЗНАЧ
Выборочная дисперсия	Dв	ДИСПР
Исправленная выборочная дисперсия	S2	ДИСП
Выборочное СКО	в	СТАНДОТКЛОНП
Исправленное выборочное СКО	S2	СТАНДОТКЛОН
Выборочный коэффициент корреляции	rв	КОРРЕЛ
Параметры линейной регрессии	k, b	ЛИНЕЙН
Коэффициент линейной регрессии	k	НАКЛОН
Свободный член регрессии	b	ОТРЕЗОК
Медиана	Ме	МЕДИАНА
Мода	Мо	МОДА
Коэффициент асимметрии	А	СКОС
Эксцесс	Е	ЭКСЦЕСС
Критические точки распределения Фишера	F	FРАСПОБР
Функция Лапласа	Ф(х)	НОРМСТРАСП – 0,5
Критические точки распределения Стьюдента	t	СТЬЮДРАСПОБР
Критические точки ХИ–квадрат распределения	2	ХИ2ОБР

в). Составление уравнений регрессии y=f(x) при помощи мастера диаграмм. В табличном процессоре Excel в меню Вставка имеется опция “Диаграмма”. При выборе этой опции появляется Мастер Диаграмм.

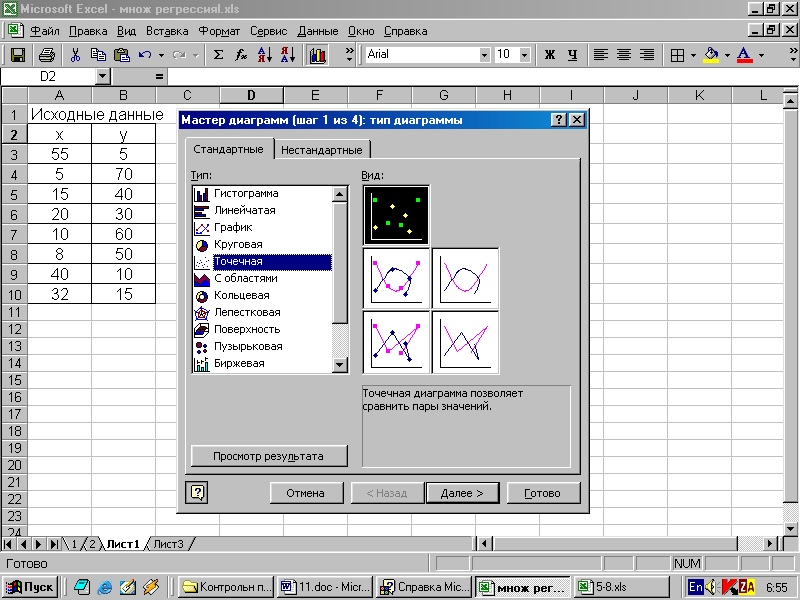
Нужно выбрать тип диаграммы – точечная; вид диаграммы - точечный рисунок без линий соединения. Далее нужно следовать указаниям мастера и в результате получается диаграмма следующего вида:

х	у
55	5
5	70
15	40
20	30
10	60
8	50
40	10
32	15

Чтобы на диаграмме появились уравнение регрессии и коэффициент детерминации R², следует выделить полученную диаграмму; в строке меню выбрать Диаграмма и в раскрывшемся меню выбрать опцию “Добавить линию тренда”. Появится диалоговое окно:

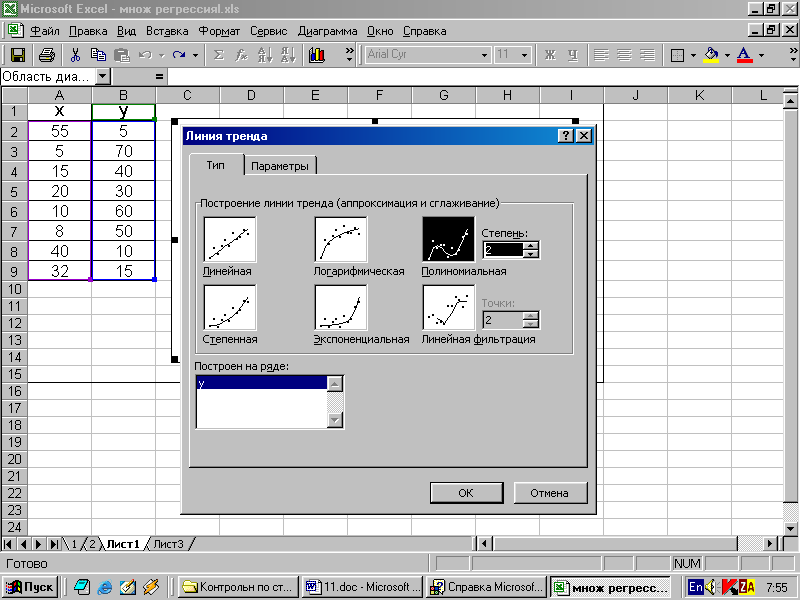
Далее нужно отметить нужный тип линии тренда, затем перейти на вкладку Параметры и выставить опции :

• Показывать уравнение на диаграмме;

• Поместить на диаграмму величину достоверности аппроксимации (R^2).

После нажатия кнопки ОК на диаграмме появится необходимая информация и она примет следующий вид:

г). Расчет статистических характеристик с помощью пакета Анализ данных. В состав Microsoft Excel входит набор средств анализа данных (так называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие средства позволяют представить результаты анализа в графическом виде.

Чтобы просмотреть список доступных инструментов анализа, нужно выбрать команду Анализ данных в меню Сервис. Появится следующий список:

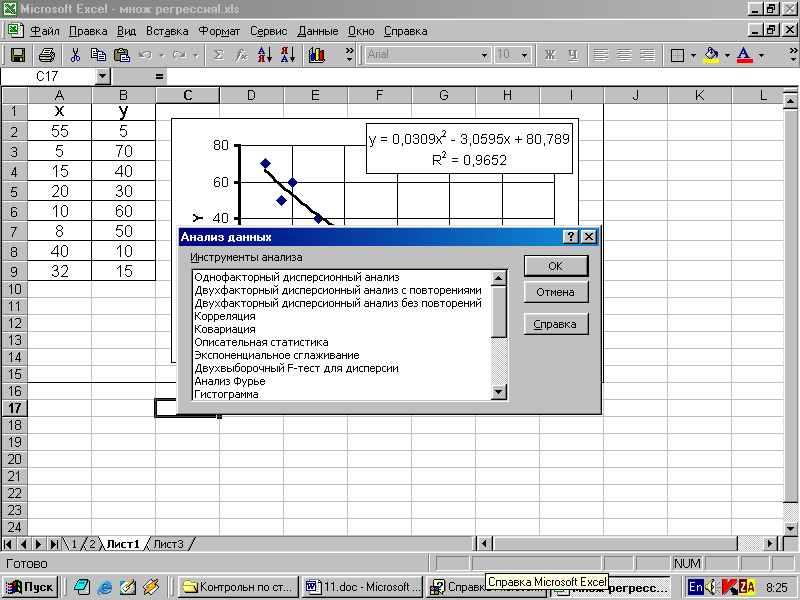
Здесь нужно выбрать необходимый раздел статистики и далее заполнить все требующиеся в открывшемся диалоговом окне формы.

В качестве примера возьмем задачу о нахождении уравнения множественной регрессии, которая решалась нами средствами пакета Mathcad в пункте 5.8. После ввода исходных данных в Excel и обращению к пакету Анализ данных выбирается раздел Регрессия. В появившейся форме вводятся диапазоны массивов: Y (результативный признак) и Х ( признаки Х₁ и Х₂ ). Далее отмечаются нужные параметры вывода. Отметим, что кроме основных статистик пользователь может получить и такие параметры как остатки, график остатков, график нормальной вероятности. После нажатия кнопки ОК компьютер выдает итоги расчетов примерно в такой форме:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,782
R-квадрат	0,612
Нормированный R-квадрат	0,566
Стандартная ошибка	7,373
Наблюдения	20
Дисперсионный анализ
	df	SS	MS	F
Регрессия	2	1455,798	727,9	13,39
Остаток	17	924,189	54,36
Итого	19	2379,987
	Коэффи циенты	Стандартная ошибка	t-стати стика	P-Зна чение
Y-пересечение	10,986	12,145	0,905	0,378
X1	23,471	8,412	2,790	0,013
X2	-0,018	0,006	-3,007	0,008

Отсюда выписываем уравнение множественной регрессии и все необходимые коэффициенты:

1) Уравнение линейной регрессии имеет вид:

2) Коэффициент детерминации равен R² = 0,612.

3) Корреляционное отношение равно R = 0,782.

4) Наблюдаемое значение критерия Фишера равно F=13,389 .

В итоге получили результаты, совпадающие с найденными ранее (п.5.8).