Обработка результатов опыта
1. Заполнить строки Р и M табл.2.
Р n,n.+1 = Р n.+1 - Рn, - приращение величины усилия, приложенного к рычагу;
М = P R - приращение изгибающего момента на этапе нагружения,
R - длина рычага 3 (рис. 8.2).
2. Заполнить строки Bi табл.2:
Вn,n+1 = Вn+1 Вn.
3. Заполнить последний столбец.табл.2. Значения определяются как среднеарифметическое приращения каждого прибора.
4. Определить нормальные напряжения в поперечном сечении балки при чистом изгибе. Величины нормальных напряжений определяют по формуле
Е - модуль продольной упругости материала балки:
Е = 0,7105Н/мм2,
К - коэффициент чувствительности тенэодатчиков.
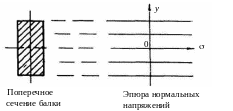5.
Построить эпюру распределения нормальных
напряжений по высоте поперечного сечения
балки.
6.Написать краткие выводы о характере эпюры нормальных напряжений.
Лабораторная работа № 8,б
Перемещения статически определимых балок при прямом изгибе
Цель работы: 1. Определение прогибов и углов поворота двухопорвой балки.
2.Определение прогибов консольных балок.
3.Проверка теоремы о взаимности перемещений.
4.Сравнение жесткости консольных балок.
Задача работы:
1. Определить экспериментально и теоретически ( и сопоставить их между собой) перемещения различных балок.
На основании 1 настольной лабораторной установки закрепленаполоса 2 прямоугольного поперечного сечения (рис.8.5,а), представляющая собой балку на двух опорах. В колонках 3 жестко защемлены консольные балки (рис.8.5,б), выполненные из стальных двухтавров в повернутые относительно друг друга на 90. Все балки снабжены подвижными каретками 5 и гиредержателями б, позволяющими проводить нагружекия в требуемых сечениях. Описание установки (рис.8.4)
4
7
8
5
4
3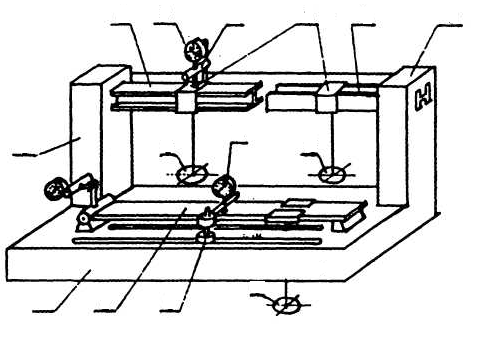
3
6
7
6
1
2
8
Р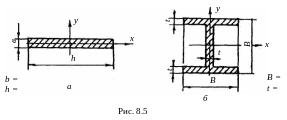
ис.8.4.
Лабораторная установка УТМ-13
Величины прогибов балок измеряются индикаторами, закрепленными в подвижных стойках 8. Цена деления индикаторов 0,01 мм. Угол поворота левого конца балки на двух опорах измеряется индикатором при помощи рычага l = 57,3 мм. Так как переводной коэффициент радианной меры угла в градусную равен 57,3, цена деления индикатора получается равной 0.01 градуса. Установка; снабжена комплектом гирь из пяти штук весом по 5 Н каждая.
Теоретические значения перемещений
Теоретические значения прогибов и углов поворота вычислим по формуле Симпсона.
Для вычисления прогиба в середине пролета балки на двух опорах
(рис 8 6,а ) строим грузовую (рис.8.6,б) и единичную (рис.8.6,в) эпюры изгибающих моментов. Тогда по формуле Симпсона
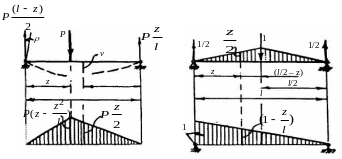
Рис. 8.6
То же самое по методу начальных параметров
при Zc= 1, V = 0
при Zp = l/2, 0 = Pl2/ 16EJ.
при Zc= l/2,
Для вычисления угла поворота опорного сечения строим соответствующую единичную эпюру (рис.8.6, г). По формуле Симпсона
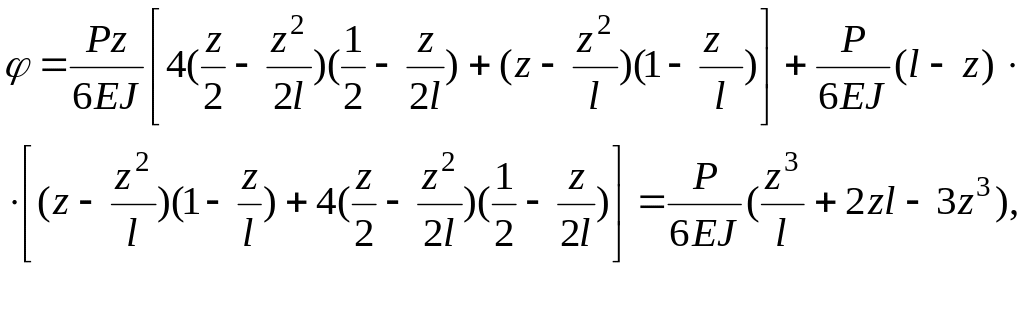
При Z = l/2 , = Pl2/16EJ.
По методу начальных параметров это значение уже определено как 0.
Для вычисления прогиба в произвольном сечении консольной балки (рис.8.7, а) строим грузовую (рис.8.7, б) и единичную (рвс.8.7, в) эпюры изгибающих моментов.
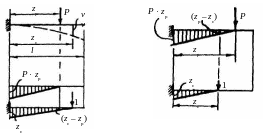
Рис.8.7
Тогда
при Zp= l/2, Zc= 1, Vl = 5Pl3/48EJ,
при Zp= l, Zc= 1, Vl = Vmax = Pl3/3EJ.
По методу начальных параметров
М0=
PZp,
P0
= P,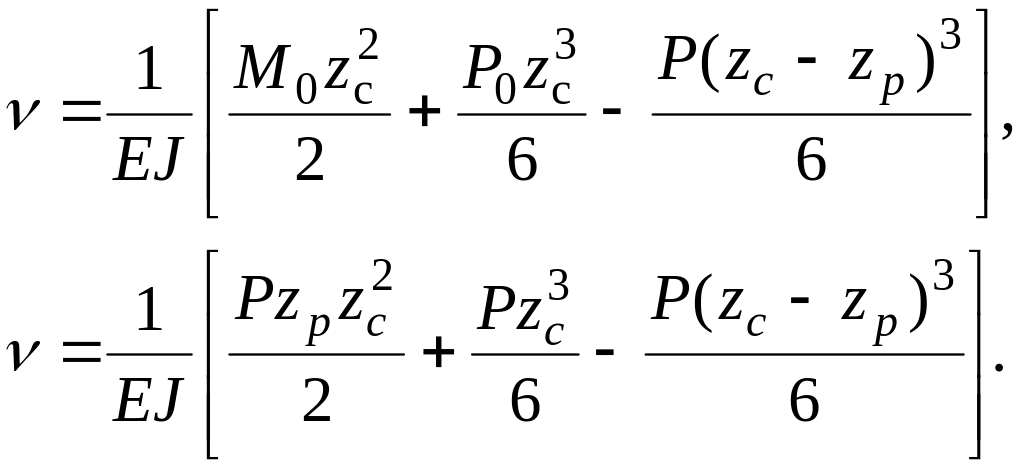
при Zp= l/2, Zc= 1, Vl = 5Pl3/48EJ,
при Zp= l, Zc= 1, Vl = Vmax = Pl3/3EJ,
При положении силы Р правее сечения, в котором нужно определить прогиб (рис.8.7, г).
при Zp= l, Zc= l/2, Vl/2 = 5Pl3/48EJ =Vl
при Zp= l/2, Zc= 1.
По методу начальных параметров
при Zp= l, Zc= l/2, Vl/2 = 5Pl3/48EJ =Vl,
при Zp= l/2, Zc= 1.
Теорема о взаимности перемещений выполняется.
Произведение EJ называется жесткостью балки при изгибе. Для одного и того же поперечного сечения момент инерции зависит от ориентации главных осей инерции по отношению к силовой плоскости. Так для двутаврового сечения (рис.8.5, б)
Jx
>
Jy
и
при одинаковой нагрузке. Зная значения моментов инерции, можно определить отношение жесткостей
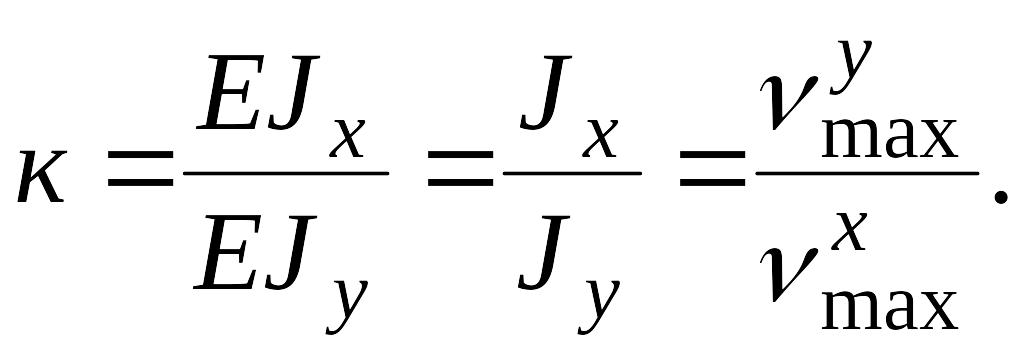
Теоретическое отношение жесткостей определяется из выражения
а экспериментальное из
