Определения

Определение 5. Пусть дано семейство случайных величин  , так что  . Тогда эти случайные величины попарно независимы, если попарно независимы порождённые ими сигма-алгебры  . Случайные величины независимы в совокупности, если таковы порождённые ими сигма-алгебры.

Определение, данное выше, эквивалентно любому другому из нижеперечисленных. Две случайные величины   независимы тогда и только тогда, когда:

• Для любых  :

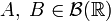• Для любых борелевских функций 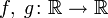  случайные величины 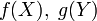 независимы.

• Для любых ограниченных борелевских функций  :

Свойства независимых случайных величин

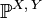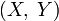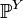• Пусть   — распределение случайного вектора  ,   — распределение   и   — распределение 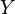 . Тогда   независимы тогда и только тогда, когда

где   обозначает (прямое) произведение мер.

• Пусть 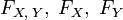  — кумулятивные функции распределения  соответственно. Тогда   независимы тогда и только тогда, когда

• Пусть случайные величины   дискретны. Тогда они независимы тогда и только тогда, когда

• Пусть случайные величины   совместно абсолютно непрерывны, то есть их совместное распределение имеет плотность 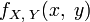 . Тогда они независимы тогда и только тогда, когда

,

где   — плотности случайных величин   и   соответственно.

Условная вероятность

Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.

Определения

Пусть   — фиксированное вероятностное пространство. Пусть   два случайных события, причём  . Тогда условной вероятностью события   при условии события   называется .

Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое конечное число испытаний, при котором с любой заданной наперёд вероятностью меньше 1 относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Общий смысл закона больших чисел — совместное действие большого числа одинаковых и независимых случайных факторов приводит к результату, в пределе не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Слабый закон больших чисел

Пусть есть бесконечная последовательность (последовательное перечисление) одинаково распределённых и некоррелированных случайных величин  , определённых на одном вероятностном пространстве  . То есть их ковариация  . Пусть  . Обозначим   выборочное среднее первых   членов:

.

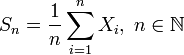Тогда  .

То есть для всякого положительного  ,

Усиленый закон больших чисел

Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин  , определённых на одном вероятностном пространстве  . Пусть  . Обозначим   выборочное среднее первых   членов:

.

Тогда   почти всегда.

То есть

Центральная предельная теорема

Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения.

Классическая Ц.П.Т

Пусть   есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние   и  , соответственно. Пусть также

.

Тогда

 по распределению при  ,

где   — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом   выборочное среднее первых   величин, то есть  , мы можем переписать результат центральной предельной теоремы в следующем виде:

 по распределению при  .

Скорость сходимости можно оценить с помощью неравенства Берри — Эссеена.

Локальная Ц.П.Т

В предположениях классической формулировки, допустим в дополнение, что распределение случайных величин   абсолютно непрерывно, то есть оно имеет плотность. Тогда распределение   также абсолютно непрерывно, и более того,

 при  ,

где   — плотность случайной величины  , а в правой части стоит плотность стандартного нормального распределения.

16