
- •Содержание
- •Пространство элементарных событий
- •Алгебра событий
- •Вероятность
- •Определение случайной величины
- •Тождества
- •Математическое ожидание дискретного распределения
- •Математическое ожидание целочисленной величины
- •Математическое ожидание абсолютно непрерывного распределения
- •Определения
- •Свойства независимых случайных величин
Тождества
Из
свойств вероятности следует,
что ![]() ,
таких что
,
таких что ![]() :
:
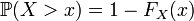 ;
;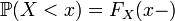 ;
;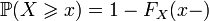 ;
;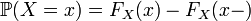 ;
;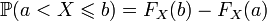 ;
;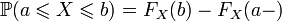 ;
;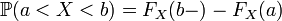 ;
;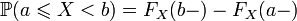 ;
;
Дискретные распределения
Если случайная величина дискретна, то есть её распределение однозначно задаётся функцией вероятности
![]() ,
,
то функция распределения этой случайной величины кусочно-постоянна и может быть записана как:
![]() .
.
Эта
функция непрерывна во всех точках
,
таких что ![]() ,
и имеет разрыв первого рода в точках
,
и имеет разрыв первого рода в точках ![]() .
.
Непрерывные распределения
Распределение называется непрерывным, если такова его функция распределения . В этом случае:
![]() ,
,
и
![]() ,
,
а следовательно формулы имеют вид:
![]() ,
,
где ![]() означает
любой интервал, открытый или закрытый,
конечный или бесконечный.
означает
любой интервал, открытый или закрытый,
конечный или бесконечный.
Абсолютно непрерывные распределения
Распределение
называется абсолютно
непрерывным, если существует
неотрицательная почти
всюду (относительно меры
Лебега) функция ![]() ,
такая что:
,
такая что:
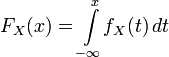 .
.
Функция ![]() называется плотностью
распределения. Известно, что функция
абсолютно непрерывного распределения
непрерывна, и, более того, если
называется плотностью
распределения. Известно, что функция
абсолютно непрерывного распределения
непрерывна, и, более того, если ![]() ,
то
,
то ![]() ,
и
,
и
![]() .
.
Математи́ческое
ожида́ние — среднее
значение случайной
величины,
распределение вероятностей случайной
величины рассматривается в теории
вероятностей.
В англоязычной литературе обозначается
через ![]() (например,
от англ. Expected
value или
нем. Erwartungswert),
в русской —
(например,
от англ. Expected
value или
нем. Erwartungswert),
в русской — ![]() (возможно,
от англ. Mean
value или нем. Mittelwert,
а возможно от «Математическое ожидание»).
В статистике часто используют
обозначение
(возможно,
от англ. Mean
value или нем. Mittelwert,
а возможно от «Математическое ожидание»).
В статистике часто используют
обозначение ![]() .
.
Определение
Пусть задано вероятностное пространство и определённая на нём случайная величина . То есть, по определению, — измеримая функция. Если существует интеграл Лебега от по пространству , то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается или .
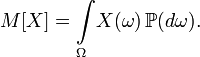
Основные формулы для математического ожидания
Если — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:
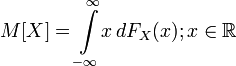 .
.
Математическое ожидание дискретного распределения
Если — дискретная случайная величина, имеющая распределение
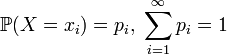 ,
,
то прямо из определения интеграла Лебега следует, что
![]() .
.
Математическое ожидание целочисленной величины
Если — положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей
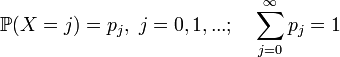
то
её математическое ожидание может быть
выражено через производящую
функцию последовательности ![]()
![]()
как
значение первой производной в единице: ![]() .
Если математическое ожидание
бесконечно,
то
.
Если математическое ожидание
бесконечно,
то ![]() и
мы будем писать
и
мы будем писать ![]()
Теперь
возьмём производящую функцию ![]() последовательности
«хвостов» распределения
последовательности
«хвостов» распределения ![]()
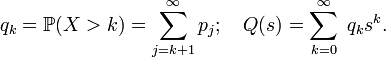
Эта
производящая функция связана с
определённой ранее функцией ![]() свойством:
свойством: ![]() при
при ![]() .
Из этого по теореме
о среднем следует,
что математическое ожидание равно
просто значению этой функции в единице:
.
Из этого по теореме
о среднем следует,
что математическое ожидание равно
просто значению этой функции в единице:
![]()
Математическое ожидание абсолютно непрерывного распределения
Математическое ожидание абсолютно непрерывной случайной величины, распределение которой задаётся плотностью , равно
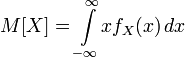 .
.
Диспе́рсия
случа́йной величины́ —
мера разброса данной случайной
величины, то есть её отклонения
от математического
ожидания. Обозначается ![]() в
русской литературе и
в
русской литературе и ![]() (англ. variance)
в зарубежной. В статистике часто
употребляется обозначение
(англ. variance)
в зарубежной. В статистике часто
употребляется обозначение ![]() или
или ![]() .
Квадратный корень из дисперсии, равный
,
называется среднеквадрати́чным
отклоне́нием, станда́ртным отклоне́нием или
стандартным разбросом. Стандартное
отклонение измеряется в тех же единицах,
что и сама случайная величина, а дисперсия
измеряется в квадратах этой единицы
измерения.
.
Квадратный корень из дисперсии, равный
,
называется среднеквадрати́чным
отклоне́нием, станда́ртным отклоне́нием или
стандартным разбросом. Стандартное
отклонение измеряется в тех же единицах,
что и сама случайная величина, а дисперсия
измеряется в квадратах этой единицы
измерения.
Из неравенства Чебышёва следует, что вероятность того, что случайная величина отстоит от своего математического ожидания более чем на k стандартных отклонений, составляет менее 1/k². Так, например, как минимум в 95 % случаев случайная величина, имеющая нормальное распределение, удалена от её среднего не более чем на два стандартных отклонения, а в примерно 99,7 % — не более чем на три.
Определение
Пусть — случайная величина, определённая на некотором вероятностном пространстве. Тогда
![]()
где
символ ![]() обозначает математическое
ожидание.
обозначает математическое
ожидание.
Свойства
Дисперсия любой случайной величины неотрицательна:
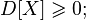
Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;
Если случайная величина равна константе, то её дисперсия равна нулю:
 Верно
и обратное: если
Верно
и обратное: если 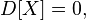 то
то 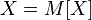 почти
всюду;
почти
всюду;Дисперсия суммы двух случайных величин равна:
![]() ,
где
,
где ![]() —
их ковариация;
—
их ковариация;
Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:
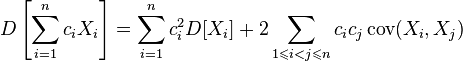 ,
где
,
где ![]() ;
;
В частности,
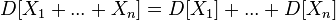 для
любых независимых
или некоррелированных случайных
величин, так как их ковариации равны
нулю;
для
любых независимых
или некоррелированных случайных
величин, так как их ковариации равны
нулю;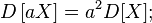
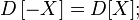
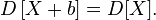
Независимость
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величиныназывают зависимыми, если значение одной из них влияет на вероятность значений другой.
Независимые события
Будем считать, что дано фиксированное вероятностное пространство .
Определение 1. Два события независимы, если
Вероятность появления события A не меняет вероятности события B.
Замечание 1. В том случае, если вероятность одного события, скажем , ненулевая, то есть , определение независимости эквивалентно:
то есть условная вероятность события при условии равна безусловной вероятности события .
Определение 2. Пусть есть семейство (конечное или бесконечное) случайных событий , где — произвольное индексное множество. Тогда эти события попарно независимы, если любые два события из этого семейства независимы, то есть
Определение 3. Пусть есть семейство (конечное или бесконечное) случайных событий . Тогда эти события совместно независимы, если для любого конечного набора этих событий верно:
Замечание 2. Совместная независимость, очевидно, влечет попарную независимость. Обратное, вообще говоря, неверно.
Пример 1. Пусть брошены три уравновешенные монеты. Определим события следующим образом:
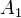 :
монеты 1 и 2 упали одной и той же стороной;
:
монеты 1 и 2 упали одной и той же стороной;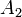 :
монеты 2 и 3 упали одной и той же стороной;
:
монеты 2 и 3 упали одной и той же стороной;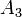 :
монеты 1 и 3 упали одной и той же стороной;
:
монеты 1 и 3 упали одной и той же стороной;
Легко
проверить, что любые два события из
этого набора независимы. Все же три в
совокупности зависимы, ибо зная, например,
что события ![]() произошли,
мы знаем точно, что
также
произошло.
произошли,
мы знаем точно, что
также
произошло.
Независимые сигма-алгебры
Определение
4. Пусть ![]() две сигма-алгебры на
одном и том же вероятностном пространстве.
Они называются независимыми,
если любые их представители независимы
между собой, то есть:
две сигма-алгебры на
одном и том же вероятностном пространстве.
Они называются независимыми,
если любые их представители независимы
между собой, то есть:
![]() .
.
Если вместо двух имеется целое семейство (возможно бесконечное) сигма-алгебр, то для него определяется попарная и совместная независимость очевидным образом.
Независимые случайные величины
