Правило ділення різниці на число
Щоб поділити різницю на число,
досить поділити на це число зменшуване
і від’ємник і від першого результату
відняти другий:
.
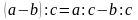Правило ділення добутку на число
Щоб поділити добуток на число,
досить поділити на це число один із
множників і результат помножити на
другий множник:
.
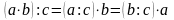Доведемо, наприклад, що
.
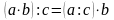Якщо ця рівність правильна, то за
означенням ділення
.
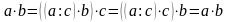Правило ділення числа на добуток
Якщо натуральнее число ділить на натуральні число і , то, щоб розділити на добуток чисел і , достатньо розділити число на і одержану частку розділити на .
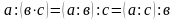
Доведення.
Припустимо що
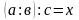(1), тоді за означенням частки
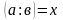звідси за означенням частки
.
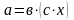На основі сполучного закону дії множення
.
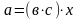А це означає, що
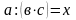(2). Таким чином
.
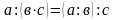На цій властивості ґрунтується послідовне
ділення при усних обчисленнях.
126 : 18 = 126 · (2 · 9) = (126 : 2) : 9 = 63 : 9 = 7
600 : 20 = 600 : (10 · 2) = (600 : 10) : 2 = 60 : 2 = 30
Правило ділення частки на число
Щоб поділити частку на число, досить поділити на це число ділене, а знайдений результат поділити на дільник або помножити дільник на це число, а потім ділене поділити на одержаний добуток.
Наприклад. 1.
.
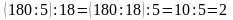2.
.
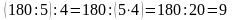Правило ділення числа на частку
Щоб поділити деяке число а
на частку від ділення двох чисел, досить
поділити це число на ділене і результат
помножити на дільник:
.
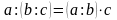Доведення. За означенням
ділення:
.
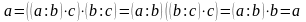Правило множення числа на частку двох чисел
Щоб помножити число на частку двох чисел достатньо помножити це число на ділене і одержаний добуток розділити на дільник
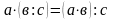
Отже,
щоб поділити суму на
число, досить поділити на це число кожний
доданок і добуті результати додати:
.
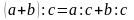Щоб поділити різницю на число, досить поділити на це число зменшуване і від’ємник і від першого результату відняти другий: .
Щоб поділити добуток на число, досить поділити на це число один із множників і результат помножити на другий множник: .
Щоб
поділити деяке число на добуток, досить
поділити це число на один із множників
і знайдену частку поділити на другий
множник:
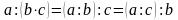
Щоб поділити частку на число, досить поділити на це число ділене, а знайдений результат поділити на дільник або помножити дільник на це число, а потім ділене поділити на одержаний добуток.
Щоб поділити деяке число а на частку від ділення двох чисел, досить поділити це число на ділене і результат помножити на дільник: .
Питання для узагальнення
Як поділити суму на число?
Яке правило ділення добутку на число?
ІІІ. Заключна частина
Загальний висновок
Дія, за допомогою якої знаходиться частка а : в називається діленням, число а – ділене, в – дільник.
Є такі правила ділення: ділення суми на число, ділення різниці на число, добутку на число, ділення числа на добуток, частки на число, числа на частку.
Запитання для узагальнення студентам
Які є два види ділення?
Як називаються компоненти дії ділення?
Дайте означення частки цілого невід’ємного числа і натурального через зв’язок ділення з множенням.
Чи можна ділити на нуль?
Сформулюйте теорему про існування і єдиність частки цілого невід’ємного числа і натурального.
Які правила ділення знаєте? Сформулюйте їх.
Повідомлення домашнього завдання
Стойлова, Л. П. Основы начального курса математики [Текст] : учеб. пособие для учащихся педучилищ / Л. П. Стойлова, А. М. Пишкало. – М. : Просвещение, 1988. – C. 147 – 155.
Впр. 2, 4 (С 152), впр. 1 (С. 153).
Кухар, В. М. Теоретичні основи початкового курсу математики [Текст] : навч. посібник для педучилищ / В. М. Кухар, Б. Л. Білий. – К. : Вища школа, 1987. –С. 188 – 192.
Впр. 5, 6, 7 (С. 191).