Міністерство освіти і науки України

Комунальний вищий навчальний заклад

«Бериславський педагогічний коледж імені В. Ф. Беньковського»

Херсонської обласної ради

Предмет: Основи початкового курсу математики Модуль № 1 Семестр: V Кількість годин: 2

Лекція № 8 (49-50)

Тема: Теоретико-множинний зміст частки двох цілих невід’ємних чисел

Розглянуто і затверджено на засіданні предметної (циклової) комісії викладачів фізико-математичних дисциплін та нових інформаційних технологій Протокол № ___ від _________ 2013р. Голова предметної (циклової) комісії: _________________ Г. Ю. Шкворченко

м. Берислав

Тема лекції: Теоретико-множинний зміст частки двох цілих невід’ємних чисел

Студенти повинні знати:

• означення частки цілих невід’ємних чисел;

• компоненти дії ділення;

• закони ділення;

• правила ділення суми на число, числа на добуток, добутку на число.

Студенти повинні вміти:

• виконувати ділення цілих невід’ємних чисел;

• застосовувати правила ділення з метою раціоналізації обчислень.

Тип лекції: тематична

Ключові поняття: частка цілих невід’ємних чисел, компоненти дії ділення (ділене, дільник, частка), правила ділення суми на число, числа на добуток, добутку на число.

План

1. Теоретико-множинний зміст частки цілого невід’ємного числа і натурального.

2. Визначення частки через добуток.

3. Існування частки, її єдність.

4. Теоретичне обгрунтування неможливості ділення на нуль.

5. Правила ділення.

Основна література

1. Кухар, В. М. Теоретичні основи початкового курсу математики [Текст] : навч. посібник для педучилищ / В. М. Кухар, Б. Л. Білий. – К. : Вища школа, 1987. – С. 188-192.

2. Основи початкового курсу математики [Текст] : навчально-методичний посібник / укл. Л. М. Голець, О. О. Кислякова, І. А. Ляшенко, О. Г. Онуфрієнко. – Запоріжжя, 2010. –

С. 67-71.

3. Стойлова, Л. П. Основы начального курса математики [Текст] : учеб. пособие для учащихся педучилищ / Л. П. Стойлова, А. М. Пишкало. – М. : Просвещение, 1988. – С. 147-154.

Інтернет-ресурси

1. Деление и его свойства [Электронный ресурс] : теоретические материалы // сайт shkolo.ru. – Режим доступа: http://shkolo.ru/delenie-i-ego-svoystva. – Название с экрана.

2. Деление с остатком [Электронный ресурс] : теоретические материалы // сайт shkolo.ru. – Режим доступа: http://shkolo.ru/delenie-s-ostatkom. – Название с экрана.

3. Умножение и деление на разрядную единицу [Электронный ресурс] : теоретические материалы // сайт shkolo.ru. – Режим доступа: http://shkolo.ru/umnozhenie-i-delenie-na-razryadnuyu-edinitsu. – Название с экрана.

Структура лекції

І. Вступна частина:

1. Оголошення теми, мети і завдань лекції.

2. Ознайомлення з планом лекції, основною та додатковою літературою.

ІІ. Виклад лекційного матеріалу (згідно плану та вимог до лекції)

1. Теоретико-множинний зміст частки цілого невід’ємного числа і натурального

На практиці часто доводиться розв’язувати такі задачі:

Задача 1. 8 апельсинів розклали на дві тарілки порівну. По скільки апельсинів буде на кожній тарілці?

Аналіз. В задачі розглядається множина А в якій 8 елементів 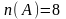. Множину А розбито на дві рівнопотужні підмножини

А ○○○○○○○○

1 тарілка ○○○○

2 тарілка ○○○○

тоді 8 : 2 – це кількість елементів в кожній підмножині

8 : 2 = 4 (ап.)

Такі задачі називають «задачами на ділення на рівні частини».

Задача 2. 8 апельсинів розклали по 2 апельсина на кожну тарілку. Скільки потрібно тарілок?

Аналіз. В цій задачі розглядається множина А в якій 8 елементів,

А ○○○○○○○○

Вона розбивається на підмножини, в кожній з яких по 2 елементи, тобто на рівнопотужні множини

А

○○ ○○ ○○ ○○

2 2 2 2

В задачі питається «скільки таких підмножин одержимо?»

Отже 8 : 2 – це число двоелементних підмножин, на які розбито множину з 8 елементів.

Такі задачі називають «задачами на ділення на вміщення».

Обидві задачі розв’язуються одним і тим же виразом 8 : 2, але цей вираз має різні значення.

В загальному випадку частку цілого невід’ємного числа а і натурального числа в визначають таким чином.

Означення 1. Неха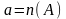й і множину А розбито на попарнонеперетинаючі рівнопотужні підмножини.

Якщо в – це число підмножин в розбитті множини А, то часткою чисел а і в називається число елементів кожної підмножини.

Якщо в – число елементів кожної підмножини в розбитті множини А, то часткою чисел а і в називається число підмножин в цьому розбитті.

Дія, за допомогою якої знаходиться частка а : в називається діленням, число а – ділене, в – дільник.

Отже, З теоретико-множинної точки зору обидві задачі приводять до подання скінченної множини А у вигляді об’єднання еквівалентних між собою (без спільних елементів) її підмножин. Перехід до чисельної характеристики такої задачі приводить до розгляду дії ділення на множині цілих невід’ємних чисел.

Дія, за допомогою якої знаходиться частка а : в називається діленням, число а – ділене, в – дільник.

Питання для узагальнення

• Які є два види ділення?

• Як називаються компоненти дії ділення?