III. Применение теории статистических решений
3.1. Определение целесообразности местного поиска
Методику решения задач теории статистических решений рассмотрим на примере задачи о целесообразности местного поиска.
В этой ситуации учитываются следующие показатели работы:
Т – время неизменности промысловой обстановки, т.е. время в течение которого будет вестись добыча новых уловов, если они есть в районе или сохранятся старые уловы при неуспешном поиске
а – средний улов в единицу времени при существующей обстановке без обнаружения больших уловов
а’ – средние уловы, если обнаружены новые или лучшие скопления рыбы, т.е. при успешном поиске
р – вероятность успешного поиска т.е. вероятность наличия лучших скоплений в районе и успешного их обнаружения за время tп
tп – время поиска для успешного обнаружения лучших скоплений.
Действие судна: S1 продолжать работу без поиска, S2 - поиск длительностью tп и дальнейшие действия с учетом результатов поиска.
Действие природы: 1 – в районе поиска есть лучшие скопления, дающие хорошие уловы, 2 – нет лучших скоплений.
С математической точки зрения задача выбора действий при двух состояниях природы называется задачей проверки гипотез, ее решение выполняется в следующем порядке:
Составляется матрица добычи, т.е. уловов за время Т при соответствующих действиях рыбака и природы.
Таблица 6
-
П р
S1
S2
1
аТ
(Т- tп)* а’
2
аТ
(Т- tп)* а
2. Переводим матрицу добычи в матрицу сожалений. в данной задаче это недоловы, которые будут иметь судно, если выберет способ действия не соответствующие состоянию природы. При этом учтем, что задача о поиске имеет смысл, если а’> а; tп<<Т.
Поэтому матрица улова будет иметь вид:
Таблица 7
-
П р
S1
S2
1
(Т- tп)* а’-аТ
0
2
0
(-(Т- tп)* а+аТ)=аtп
3. Для выбора лучшего действия определяют риски при сожалениях. Риски - это потери стороны действующей определенным образом с учетом состояния природы. В рассматриваемой задаче 1 имеет вероятность Р, а состояние 2 имеет вероятность 1-Р.
В итоге риск при действии S1 :
W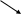
1=(T-tп)*а-аТ*Р+0(1-Р)
0
р
иск
при действии S2
:
W2= 0 *Р+аtп(1-Р)= аtп(1-Р)
0
4. Лучшее действие – риски которых меньше.
Поэтому целесообразность местного поиска в виде действия S2 предпочтительна, если
(3.1.1.)
Величина W характеризует относительное предпочтение действий S2 перед S1.
В реальных условиях капитан судна может принять решение о целесообразности местного поиска при W=1,5-2,0, если он азартный человек. Осторожный капитан может принимать решение при W>10 единиц.
Определив по опыту при каких значениях W в данном районе местный поиск целесообразен, можно решить задачи о min допустимых величинных промысловой обстановки при которых местный поиск целесообразен с заданными значениями W.
(3.1.2)
(3.1.3)
(3.1.4)
(3.1.5)
Pд – вероятность обнаружения лучших скоплений допустимая
(3.1.6)
(3.1.7)
G – среднее величина добычи за время Т при работе с поиском