
3. Контрольные вопросы
1. Сформулируйте определения сходящегося числового ряда, суммы
ряда, остатка ряда.
2. Какой ряд называется расходящимся? Приведите примеры сходя-
щихся и расходящихся рядов.
3. Сформулируйте критерий Коши сходимости числового ряда. В чем
состоит необходимый признак сходимости?
4. Какой ряд называется знакоположительным? Сформулируйте основной признак сходимости.
5.Сформулируйте достаточные признаки сходимости знакоположительных рядов: признак разреженности, признаки сравнения, признак Даламбера, радикальный признак Коши и интегральный признак. Укажите условия сходимости и расходимости обобщенного гармонического ряда.
6. Верно ли, что: а) если ряд сходится, то его частичные суммы ограничены; б) если частичные суммы ограничены, то ряд сходится.
7. Существует ли ряд, который а) по признаку Даламбера сходится, а по признаку Коши расходится; б) по признаку Коши сходится, а признаку сравнения расходится.
8. Привести пример двух рядов
 и
и
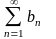 ,
для которых ряд
,
для которых ряд
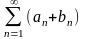 сходится,
а ряд
сходится,
а ряд
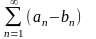 расходится.
расходится.
9. Какой ряд называется знакочередующимся? Сформулируйте признак Лейбница. В чем состоит практическое значение следствия к признаку Лейбница.
10. Верно ли, что: а) если ряд сходится абсолютно, то он сходится и условно; б) если ряд сходится условно, то он не сходится абсолютно.
11. Какой ряд называется знакопеременным? Сформулируйте достаточный признак сходимости знакопеременного ряда. В чем состоит отличие абсолютной и условной сходимости знакопеременного ряда?
12. Сформулируйте признаки Абеля и Дирихле для знакопеременных рядов.
13.Что называется функциональным рядом? Дайте определения сходящегося и равномерно сходящегося функциональных рядов. В чем состоит отличие?
14. Сформулируйте критерий Коши и признак Вейерштрасса для функциональных рядов. Приведите примеры применения.
15. Сформулируйте теорему о пределе суммы функционального ряда и теорему об её непрерывности. Приведите пример ряда с непрерывными функциями, у которого сумма является разрывной функцией.
16. Сформулируйте теоремы о дифференцировании и интегрировании функционального ряда. Приведите примеры применения.
17. Какой функциональный ряд называется степенным? Сформулируйте теорему Коши-Адамара. Какое множество является областью сходимости степенного ряда? Как его находят?
18. Сформулируйте теорему Абеля и теорему о почленном дифференцировании и интегрировании степенного ряда. Приведите пример применения последней теоремы.
19. Какой степенной ряд называется рядом Тейлора? Как определяются коэффициенты этого ряда?
20. В чем состоит необходимое и достаточное условие сходимости к своему ряду Тейлора? Только достаточное? Приведите пример функции, к которой не сходится её ряд Тейлора.
21. Запишите разложения следующих функций
в ряд Маклорена:
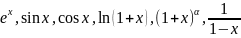 .
.
22. Что называется основной тригонометрической системой и тригонометрической системой общего вида? Что означает ортогональность этих систем?
23. Запишите тригонометрический ряд Фурье и коэффициенты Фурье по основной тригонометрической системе и по тригонометрической системе общего вида.
24. Сформулируйте свойства коэффициентов Фурье, а также лемму Римана.
25. Запишите тригонометрический ряд Фурье и коэффициенты Фурье: а) для четных функций; б) для нечетных функций
26. Сформулируйте теорему Вейерштрасса. Какими свойствами должна обладать функция, чтобы абсолютно и равномерно сходился ее ряд Фурье?
27. Запишите тригонометрический ряд Фурье в комплексной форме и коэффициенты Фурье. Приведите пример.
29. Какой вид имеет интеграл Фурье? При каких условиях интеграл Фурье сходится? Запишите интегральное преобразование Фурье.
