
1.3. Знакопеременные ряды. Числовой ряд называется знакопеременным, если его члены могут иметь как положительные, так и отрицательные знаки.
Определение. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Пример 14. Проверьте сходимость
ряда
 .
.
Решение. Рассмотрим сходящийся ряд
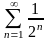 .
Понятно, что для любого
выполняется условие
.
Понятно, что для любого
выполняется условие
 .
Следовательно, ряд
сходится абсолютно по признаку сравнения,
поэтому он и просто сходится согласно
признаку сравнения.
.
Следовательно, ряд
сходится абсолютно по признаку сравнения,
поэтому он и просто сходится согласно
признаку сравнения.
Среди знакопеременных рядов большое значение имеют знакочередующиеся ряды, т.е. ряды вида
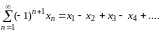 ,
,
где
 для любого
.
Такой ряд иногда называют рядом
Лейбница.
для любого
.
Такой ряд иногда называют рядом
Лейбница.
Теорема (признак Лейбница). Пусть
выполняется условие
![]() для любого
для любого
 и
и
 ,
тогда знакочередующийся ряд сходится.
,
тогда знакочередующийся ряд сходится.
Следствие. Абсолютная погрешность при замене суммы знакочередующегося ряда его частичной суммой не превосходит первого отброшенного члена ряда.
Теорема (признак Дирихле). Пусть дан
ряд
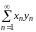 ,
такой, что последовательность
монотонно стремится к нулю, а
последовательность частичных сумм ряда
,
такой, что последовательность
монотонно стремится к нулю, а
последовательность частичных сумм ряда
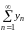 ограничена, тогда и ряд
сходится.
ограничена, тогда и ряд
сходится.
Пример 15. Исследовать
сходимость ряда
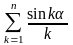 .
.
Решение. Пусть
 ,
,
 Тогда
Тогда

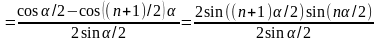 .
.
Таким образом,
 .
.
Если
 ,
то все слагаемые равны нулю и суммы
равны нулю. Таким образом,
,
то все слагаемые равны нулю и суммы
равны нулю. Таким образом,
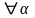 частичные суммы
частичные суммы
 ограничены. Последовательность
ограничены. Последовательность
 монотонно убывает и стремится к нулю
при
,
следовательно, по признаку Дирихле ряд
сходится.
монотонно убывает и стремится к нулю
при
,
следовательно, по признаку Дирихле ряд
сходится.
Теорема (признак Абеля) Если
последовательность
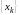 монотонна и ограничена, а ряд
сходится, то сходится и ряд
монотонна и ограничена, а ряд
сходится, то сходится и ряд
 .
.
Пример 16. Выясните сходимость
ряда
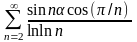 .
.
Решение. Так как ряд
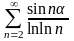 сходится по признаку Дирихле
(последовательность частичных сумм
ряда
сходится по признаку Дирихле
(последовательность частичных сумм
ряда
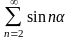 ограничена, а последовательность
ограничена, а последовательность
 монотонно) и последовательность
монотонно) и последовательность
 монотонна и ограничена, то ряд
сходится.
монотонна и ограничена, то ряд
сходится.
Задачи и упражнения
1.7. Докажите сходимость следующих рядов и найти их суммы:
1)
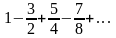 ; 2)
; 2)
 .
.
1.8. Зная, что
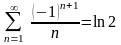 ,
найдите суммы рядов, полученных из
данного в результате перестановки его
членов:
,
найдите суммы рядов, полученных из
данного в результате перестановки его
членов:
1)
 ; 2)
; 2)
 .
.
1.9. Исследуйте сходимость знакопеременных
рядов:
1) ; 2)
; 2)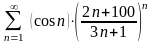 ;
;
3)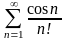 ; 4)
; 4)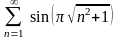 ;
;
5)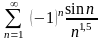 ; 6)
; 6) ;
;
7) ; 8)
; 8)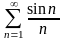 .
.
1.10. Исследуйте на абсолютную и
условную сходимость знакочередующиеся
ряды:
1)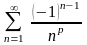 ; 2)
; 2)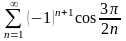 ;
;
3)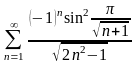 ; 4)
; 4) ;
;
5) ; 6)
; 6) ;
;
7)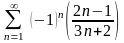 ; 8)
; 8)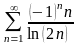 ;
;
9)
 ;
10)
;
10) ;
;
11)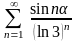 ;
12)
;
12)
 .
.
1.11. Сколько членов ряда следует
взять, чтобы получить его сумму с
точностью до
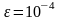 ,
если:
1)
,
если:
1)
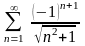 ;
2)
;
2)
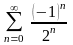 ;
3)
;
3)
 4
4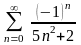 .
.
2. Функциональные ряды
2.1. Область сходимости. Множество значений аргумента x, при которых функциональный ряд
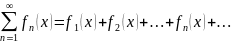
сходится, называется областью сходимостью этого ряда. Функция

где
 частичная
сумма, а x принадлежит
области сходимости, называется суммой
ряда. Функция
частичная
сумма, а x принадлежит
области сходимости, называется суммой
ряда. Функция
 называется
остатком ряда.
называется
остатком ряда.
Существует два типа сходимости
функционального ряда: поточечная и
равномерная. Функциональный ряд
 называется сходящимся на множестве
называется сходящимся на множестве
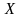 к функции
к функции
 ,
если он сходится в каждой точке множества
X , т.е.
,
если он сходится в каждой точке множества
X , т.е.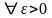
 такое, что выполняется
такое, что выполняется
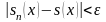
 .
.
Функциональный ряд
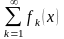 называется равномерно сходящимся на
множестве
к функции
,
если
называется равномерно сходящимся на
множестве
к функции
,
если
 такое, что
и
такое, что
и
 выполняется
.
выполняется
.
Признак Вейерштрасса равномерной
сходимости: пусть для
 и
и
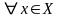 выполняются неравенства
выполняются неравенства
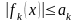 ,
причем числовой ряд
,
причем числовой ряд
 сходится.
Тогда функциональный ряд
сходится.
Тогда функциональный ряд
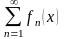 сходится абсолютно и равномерно на
множестве
сходится абсолютно и равномерно на
множестве
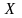 .
.
Пример 1. Исследовать
сходимость ряда
 на отрезке
на отрезке
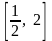 .
.
Решение. Первое слагаемое в сумме
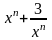 принимает наибольшее значение в точке
принимает наибольшее значение в точке
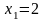 ,
второе в точке
,
второе в точке
 .
Следовательно, для всех
.
Следовательно, для всех
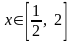 имеем, что
имеем, что
 ,
и в силу признака Вейерштрасса получаем,
что данный ряд сходится равномерно на
.
,
и в силу признака Вейерштрасса получаем,
что данный ряд сходится равномерно на
.
Для данного функционального ряда построить мажорирующий ряд и доказать равномерную сходимость на указанном отрезке.
2.1.
 2.2.
2.2.
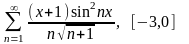
2.3.
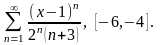 2.4.
2.4.

2.5.
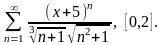 2.6.
2.6.

2.7.
 2.8.
2.8.
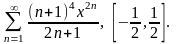
Частным случаем функционального ряда является степенной ряд, который имеет вид:

Областью сходимости степенного ряда
является интервал с центром в точке
 и
радиусом R, т.е. множество
определяемое неравенством:
и
радиусом R, т.е. множество
определяемое неравенством:
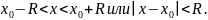 Вне этого интервала степенной ряд
расходится, а на концах, т.е. в точках
Вне этого интервала степенной ряд
расходится, а на концах, т.е. в точках
 ряд может сходиться, а может и расходиться.
Радиус сходимости R
может быть, в частных случаях равен
также 0 и
ряд может сходиться, а может и расходиться.
Радиус сходимости R
может быть, в частных случаях равен
также 0 и
 Интервал сходимости определяют обычно
с помощью признаков Даламбера или Коши.
Интервал сходимости определяют обычно
с помощью признаков Даламбера или Коши.
Во многих случаях для нахождения области сходимости функционального ряда достаточно применить к этому ряду известные признаки сходимости, считая x фиксированным числом.
Пример 2. Найти область
сходимости ряда
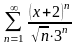 .
.
Решение. К рядам такого вида можно
применить условие сходимости Даламбера:
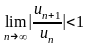 .
В нашем случае:
.
В нашем случае:
 ;
;
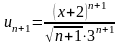 .
.
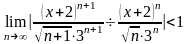 ;
; 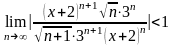 .
.
После сокращения одинаковых сомножителей получим:
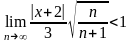 .
.
Вынесем за знак предела постоянные
множители (учитывая, что
 не зависит от
):
не зависит от
):
 .
.
Так как
 ,
,
то окончательно получим:
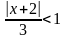 ,
или
,
или
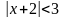 .
.
Раскрывая «модульное» неравенство,
имеем:
 , откуда
, откуда
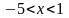 .
.
Ясно, что вторая часть теоремы Даламбера (об условиях расходимости ряда) привела бы нас при решении неравенства
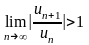
к множеству точек
 .
.
Очевидно, что точки
 и
и
 являются решениями уравнения
являются решениями уравнения
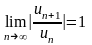 ,
а в этом случае признак Даламбера не
дает ответа на вопрос о сходимости или
расходимости ряда. Поэтому в указанных
случаях требуется проведение
дополнительного исследования сходимости
функционального ряда, для чего подставим
оба числа в исходный ряд:
,
а в этом случае признак Даламбера не
дает ответа на вопрос о сходимости или
расходимости ряда. Поэтому в указанных
случаях требуется проведение
дополнительного исследования сходимости
функционального ряда, для чего подставим
оба числа в исходный ряд:
а) . Подставив в исходный ряд, получим:
 .
.
Исследуем полученный знакочередующийся ряд с помощью признака Лейбница:
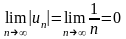
 ряд
ряд
 сходится, значит точка
сходится, значит точка
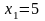
является точкой сходимости функционального ряда .
б) . Подставив в ряд, будем иметь:
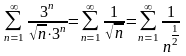 .
.
Так как
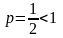 ,
то этот обобщенный гармонический ряд
расходится, т.е. точка
не является точкой сходимости исходного
функционального ряда.
,
то этот обобщенный гармонический ряд
расходится, т.е. точка
не является точкой сходимости исходного
функционального ряда.
Итак, объединяя интервал сходимости и
точку
,
получим окончательно область сходимости
исходного ряда:
 .
.
Найти область сходимости рядов:
2.9.  .
2.10.
.
2.10.  .
.
2.11.  .
2.12.
.
2.12.
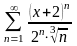 .
.
2.13.
 .
2.14.
.
2.14. 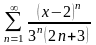 .
.
2.15. 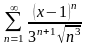 .
2.16.
.
2.16.
 .
.
2.17. 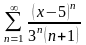 .
2.18.
.
2.18. 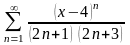 .
.
2.19.  .
2.20.
.
2.20.  .
.
2.21.  .
2.22
.
2.22 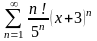 .
.
2.23.  .
2.24.
.
2.24. 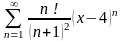 .
.
Найти область сходимости функционального ряда:
2.25.
 .
2.26.
.
2.27.
.
2.26.
.
2.27.


2.28.
 .
2.29.
.
2.29.
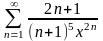 .
2.30.
.
2.30.
 .
.
2.31.
 .
2.32.
.
2.32.
 2.33.
2.33.

Теоремы о дифференцировании и интегрировании степенных рядов в некоторых случаях позволяют находить сумму ряда.
Пример 3. Найти сумму ряда
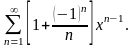
Решение.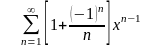 =
=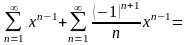
 Обозначим
Обозначим
 Тогда
Тогда


Окончательно получаем
Найти сумму ряда.
2.34.
 .
2.35.
.
2.35.

2.36.
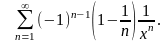 2.36.
2.36.
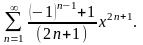
2.37.
 2.38.
2.38.
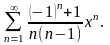
2.39.
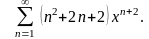 2.40.
2.40.

2.41.
 2.42.
2.42.
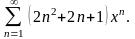
2.2. Ряд Тейлора. Если функция
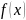 допускает
в некоторой окрестности разложение в
степенной ряд по степеням
допускает
в некоторой окрестности разложение в
степенной ряд по степеням
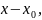 то этот ряд называется рядом Тейлора и
имеет вид:
то этот ряд называется рядом Тейлора и
имеет вид:

При
 ряд Тейлора называют также рядом
Маклорена.
ряд Тейлора называют также рядом
Маклорена.
Для оценки остаточного члена ряда можно пользоваться формулой (форма Лагранжа):
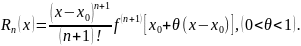
Разложения некоторых основных элементарных функций в степенной ряд имеют вид:
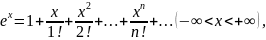




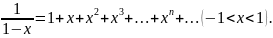
Пользуясь этими разложениями, можно во многих случаях получать разложение заданной функции в степенной ряд, причем отпадает необходимость исследования остаточного члена ряда. Иногда при разложении необходимо использовать почленное дифференцирование или интегрирование. При разложении в степенные ряды рациональных функций рекомендуется разлагать их на простейшие дроби.
Разложение функций в степенные ряды применяется при решении различных задач: нахождении пределов, приближенном вычислении значений функций, приближенном вычислению интегралов и т.п.
Пример 4. Разложить
функцию
 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки
 .
.
Решение. Ряд Тейлора имеет вид:
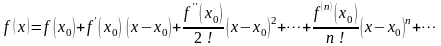 .
.
Найдем подряд несколько производных
от данной функции в точке
 :
:
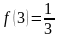 ;
;
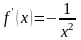 ;
;
 ;
;
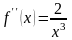 ;
;
 ;
;
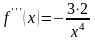 ;
;
 ;
;
 ;
;
 .
.
Подметив закономерность построения очередной производной, приходим к выводу:
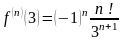 .
.
Тогда разложение данной функции в ряд Тейлора примет вид:
 .
.
Пример 5. Пользуясь
разложением функции
 в ряд Маклорена, разложить функцию
в ряд Маклорена, разложить функцию
 в окрестности точки
в окрестности точки
 .
.
Решение. Разложение функции в ряд Маклорена имеет вид:
 .
.
Тогда:
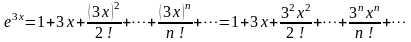 .
.
Умножив обе части этого равенства на
 ,
получим:
,
получим:
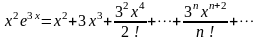 .
.
Пример 6. Пользуясь
разложением функции в ряд Маклорена,
найти седьмую производной от функции
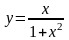 при
.
при
.
Решение. Разложим функцию в ряд Маклорена, используя стандартное разложение:
 ,
,
Тогда
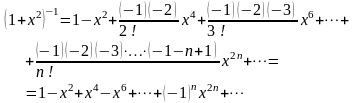
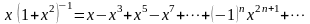 .
.
Так как в общем случае ряд Маклорена имеет вид:
 ,
,
то, сравнивая коэффициенты при
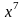 ,
будем иметь:
,
будем иметь:
 ,
отсюда
,
отсюда
 .
.
Пример 7. Вычислить
приближенное значение
 ,
взяв три члена разложения в ряд Маклорена
функции
,
взяв три члена разложения в ряд Маклорена
функции
 ,
и оценить погрешность.
,
и оценить погрешность.
Решение. Используем разложение функции в ряд Маклорена:
,
тогда точное значение будет:
 .
.
Оставив в этом разложении три члена, получим:
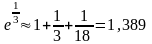 .
.
Для оценки погрешности используем остаточный член в форме Лагранжа:
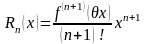 ,
где
,
где
 .
.
В нашем случае:
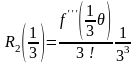 ,
где
,
где
 .
.
Так как
,
то
 ,
поэтому справедлива оценка
,
поэтому справедлива оценка
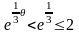 .
Тогда
.
Тогда
 .
.
Поэтому делаем вывод, что погрешность будет следующей:
 ,
,
а значит, в ответе оставляем две цифры
после запятой, т.е.
 .
.
Пример 8. Вычислить с
точностью до
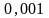 :
:
 .
.
Решение. Разложим подынтегральную
функцию в ряд Маклорена. Чтобы разложить
функцию
 ,
найдем сначала её производную:
,
найдем сначала её производную:
 .
.
Используем биноминальный ряд:
.
В нашем случае будем иметь:
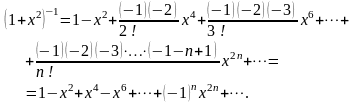
Интегрируем обе части полученного равенства:
 ;
;
 .
.
Делим обе части полученного равенства
на
 ,и
получаем
,и
получаем

Теперь интегрируем это равенство на
отрезке
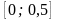 :
:
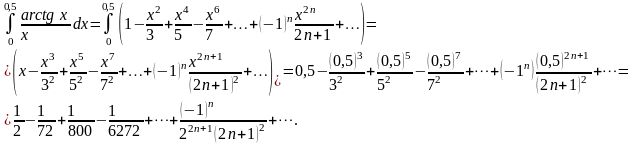
В результате, имеем сходящийся
знакочередующийся ряд, сумма которого
(следствие к признаку Лейбница) не
превосходит величины первого отброшенного
члена. Поэтому, если оставить в полученном
разложении 3 слагаемых, то величина
отброшенного остатка (который тоже
является сходящимся знакочередующимся
рядом) не будет превышать величины
своего первого члена, т.е. величины
первого отброшенного слагаемого:
 ,
а эта погрешность наверняка меньше, чем
.
,
а эта погрешность наверняка меньше, чем
.
Итак:
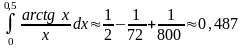 .
.
Разложить следующие функции в ряд Тейлора и исследовать остаточные члены:
2.43.
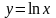 в окрестности точки
в окрестности точки
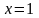 .
.
2.44.
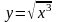 в окрестности точки
.
в окрестности точки
.
2.45.
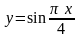 в окрестности точки
в окрестности точки
 .
.
2.46.
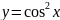 в окрестности точки
в окрестности точки
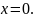
Разложить данные функции в окрестности точки , пользуясь формулами разложения в ряд Маклорена основных элементарных функций.
2.47. 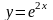 .
2.48.
.
2.48.  .
.
2.49. 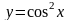 . 2.50.
. 2.50. 
2.51. 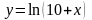 . 2.52.
. 2.52.  .
.
2.53. 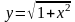 . 2.54.
. 2.54. 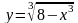 .
.
2.55. 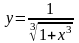 . 2.56.
. 2.56.
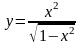 .
.
2.57.  .
2.58. y=
.
2.58. y=
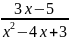
2.59. Пользуясь формулами разложения
в ряд Маклорена основных элементарных
функций, разложить по степеням
 функции:
функции:

2.60. Пользуясь разложением функции в ряд Маклорена, найти значение:
а) пятой производной от функции
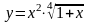 при
;
при
;
б) десятой производной от функции
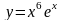 при
.
при
.
Пользуясь разложением функции в ряд Маклорена, вычислить пределы:
2.61. 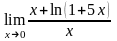 .
2.62.
.
2.62. 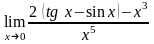 .
.
2.63.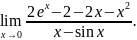 2.64.
2.64.
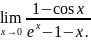 .
.
Выразить в форме ряда интегралы, используя разложение в ряд подынтегральных функций и указать области сходимости полученных рядов.
2.65.
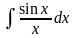 . 2.66.
. 2.66.
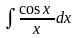 .
.
2.67.
 . 2.68.
. 2.68.
 .
.
2.69.
 . 2.70.
. 2.70.
 .
.
Вычислить приближенно с заданной точностью.
2.71.
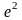 с точностью до
.
с точностью до
.
2.72.
 с точностью до
.
с точностью до
.
2.73.
 с точностью до
с точностью до
 .
.
2.74.
 с точностью до
.
с точностью до
.
2.75.
 с точностью до
с точностью до
 .
.
2.76.
 с точностью до
.
с точностью до
.
2.77.
 с точностью до
.
с точностью до
.
2.78.
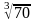 с точностью до
.
с точностью до
.
2.79.
 с точностью до
.
с точностью до
.
2.80.
 с точностью до
.
с точностью до
.
2.81.
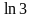 с точностью до
.
с точностью до
.
2.82.
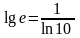 с точностью до
с точностью до
 .
.
2.83.
 с точностью до
.
с точностью до
.
2.84.
 с точностью до
.
с точностью до
.
2.85.
 с точностью до
.
с точностью до
.
2.86. Вычислить площадь,
ограниченную линией
 ,
осью ординат и прямой
,
осью ординат и прямой
 ,
с точностью до
.
,
с точностью до
.
2.87. Вычислить длину одной
полуволны синусоиды
 с точностью до
.
с точностью до
.
2.88.
Вычислить длину параболы
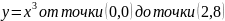 с
точностью до
.
с
точностью до
.
2.3. Тригонометрические ряды Фурье.
Тригонометрическим рядом Фурье
периодической функции
с периодом 2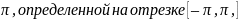 называется функциональный ряд
называется функциональный ряд

где числа
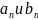 называются
коэффициентами Фурье и определяются
по формулам:
называются
коэффициентами Фурье и определяются
по формулам:


Теорема Дирихле. Пусть функция
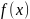 удовлетворяет условиям:
удовлетворяет условиям:
равномерно ограничена в интервале
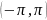 ,
т.е.
,
т.е.
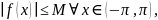 где М – постоянная;
где М – постоянная;имеет не более чем конечное число точек разрыва 1-го рода;
имеет не более чем конечное число точек строгого экстремума.
Тогда формально составленный ряд Фурье
этой функции сходится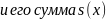 является периодической функцией с
периодом
является периодической функцией с
периодом
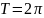 ,
причем в точках непрерывности
,
причем в точках непрерывности
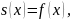 а в точках разрыва
а в точках разрыва
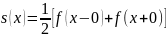 .
.
Если функция
задана на отрезке
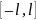 ,
где
,
где
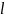 -
произвольное число, то при выполнении
условий Дирихле на этом отрезке, указанная
функция может быть представлена в виде
суммы ряда Фурье
-
произвольное число, то при выполнении
условий Дирихле на этом отрезке, указанная
функция может быть представлена в виде
суммы ряда Фурье
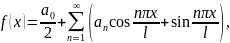
где

В случае, когда
-
четная функция в интервале
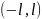 ,
то её ряд Фурье имеет вид:
,
то её ряд Фурье имеет вид:

Если - нечетная функция в интервале , то её ряд Фурье имеет вид:
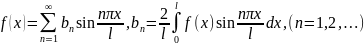
Пример 9. Разложить в ряд
Фурье периодическую функцию
 с периодом
с периодом
 :
:
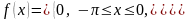
Решение. Построим график функции (рис.2.1):

Очевидно, что условия Дирихле выполняются. Определим коэффициенты Фурье:
 ;
;

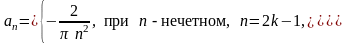

Составим ряд Фурье:
 ,
,
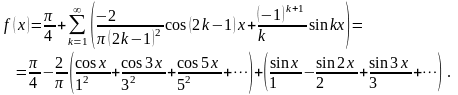
Сумма ряда

Пример 10. Разложить в ряд
Фурье периодическую с периодом
функцию
:

Решение. Построим график функции (рис.2.2):

Ясно, что
- нечетная функция,
поэтому
 ;
;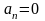 ;
;

Итак, ряд Фурье будет иметь вид:
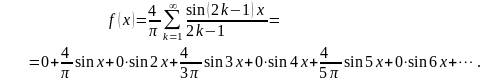 Пример 11. Разложить
в ряд Фурье периодическую функцию
Пример 11. Разложить
в ряд Фурье периодическую функцию
 ,
если
,
если
 .
.
Решение. Построим график функции (рис.2.3):

Так как,
- нечетная функция,
то
;
;
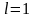 ;
;
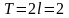 ;
;




Получим ряд Фурье:

Пример 12. Разложить функцию
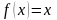 на отрезке
на отрезке
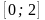 в ряд по косинусам.
в ряд по косинусам.
Решение. Продолжим эту функцию
четным образом на отрезок (рис.2.4). Получим
(рис.2.4). Получим
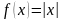 ,
,
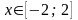 ,
,
 .
.
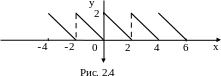
Так как
‑ четная, то
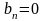 .
.
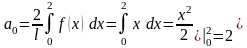 ;
;
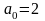 ;
;
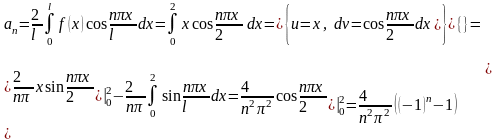
Получим ряд Фурье:
 ;
;
 .
.
Разложить следующие функции в ряд Фурье.
2.89.  ,
,
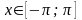
2.90. , , .
2.91. , , .
2.92.  ,
,
.
,
,
.
2.93. Периодическая с
функция

2.94. Периодическая с
функция
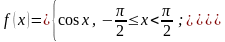
2.95.  ,
,
.
,
,
.
2.96. 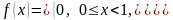
 .
.
2.97. 
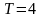 .
.
2.98. Разложите заданную функцию на указанном интервале в тригонометрический ряд: а) только по косинусам, б) только по синусам

2.99. Разложите заданную функцию на указанном интервале в тригонометрический ряд: а) только по косинусам, б) только по синусам
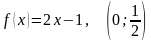
2.100. Постройте график функции , разложите заданную функцию на указанном промежутке в тригонометрический ряд Фурье
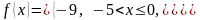
2.101. Постройте график функции , разложите заданную функцию на указанном промежутке в тригонометрический ряд Фурье

2.102. на отрезке . Разложить в ряд в ряд по синусам.
2.103.
 на отрезке
на отрезке
 .
Разложить в ряд по
синусам.
.
Разложить в ряд по
синусам.
2.104.
 на отрезке
.
Разложить в ряд по косинусам
на отрезке
.
Разложить в ряд по косинусам
 .
.
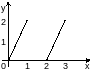 2.105. Разложите функцию
,
заданную на интервале
2.105. Разложите функцию
,
заданную на интервале
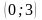 графически, в тригонометрический ряд
Фурье: а) только по косинусам, б) только
по синусам
графически, в тригонометрический ряд
Фурье: а) только по косинусам, б) только
по синусам
 2.106. Разложите функцию
,
заданную на интервале
графически, в тригонометрический ряд
Фурье: а) только по косинусам, б) только
по синусам
2.106. Разложите функцию
,
заданную на интервале
графически, в тригонометрический ряд
Фурье: а) только по косинусам, б) только
по синусам
