4.3. Дисперсійний аналіз

Розглянутий метод двовибіркового тестування розбіжностей середніх перетинається з методом дисперсійного аналізу, в яко­му аналогічна нульова гіпотеза висувається не для двох, а для /и-вибірок, кожна з яких представляє ідентифіковану у певний спосіб групу: Я_о : J, = х₂ = ...х_т . Тестування такої гіпотези ґрун­тується на порівнянні дисперсій, звідси і назва методу Диспер­сійний аналіз.

Сутність дисперсійного аналізу полягає в декомпозиції ва­ріації показника за джерелами формування. Кількість джерел варіації залежить від кількості факторів, за якими виокремлено групи. В однофакторному дисперсійному аналізі (скорочено ANOVA) виокремлюються дві компоненти варіації:

• міжгрупова, зумовлена дією фактору, покладеного в ос­ нову групування;

• внутрішньогрупова, випадкова варіація.

Основну тотожність однофакторного дисперсійного аналізу можна подати як взаємозв'язок між сумами квадратів відхилень:

Q = Qb + Qw,

т ⁿj т т ^п}

^аб°

де Q - сума квадратів відхилень окремих спостережень Ху від загальної середньої х ;

Qb - сума квадратів відхилень групових середніх Xj від за­гальної х (between);

Qw - сума квадратів відхилень окремих спостережень щ всередині груп від групових середніх (within);

nj - кількість спостережень у у-й групі; т - кількість груп, п = щт - загальна кількість спостережень.

На основі сум квадратів відхилень розраховуються три оцінки дисперсій за джерелами варіації:

я-1

міжгрупова _s\ = ', т-\

внутрішньогрупова

п-т

Знаменники оцінок дисперсії є ступенями свободи відповід­них джерел варіації. Очевидно, вони співвідносяться так само, як суми квадратів відхилень:

(п-і) = (т-\) + (п-т).

Перевірка нульової гіпотези в однофакторному дисперсій­ному аналізі ґрунтується на співвідношенні міжгрупової і внут-рішньогрупової варіації (в розрахунку на одну ступінь свободи). F-тест показує, у скільки разів оцінка міжгрупової варіації пере­вищує випадкову

UY

Q .

загальна

F =

Схема однофакторного дисперсійного аналізу подана в табл. 4.3.1.

Критичні значення F-тесту для рівня істотності а визнача­ються співвідношенням чисел ступенів свободи чисельника (т -1) і знаменника (п - т). Процедура тестування стандартна: коли F> F_x__a(m-\;n-m), нульова гіпотеза відхиляється. Якщо F<F_x__a(m-\;n-m), підстав для відхилення нульової гіпотези немає.

Тестування гіпотези щодо тотожності вибіркових середніх в пакеті Анализ данньїх здійснюється за опцією Однофакторньій дисперсионний анализ. Масив первинних даних об'єднує не менше двох суміжних діапазонів, які представляють виокремлені групи. Якщо чисельності груп неоднакові, діапазони даних бу­дуть різної довжини. У таких випадках усі діапазони виділяють до рівня найдовшого. Окрім єдиного вхідного інтервалу даних, усі інші аргументи діалогового вікна Однофакторного диспер-

сионного анализа такі самі, як Двохвьіборочного t-mecma (рис.4.2.1).

Таблиця 4.3.1. Схема однофакторного дисперсійного аналізу

Джерела варіації	Сума квадратів відхилень	Число ступенів свободи	Середній квадрат відхилень	F-тєст
Між групами	т ^njixj-I)2 7=1	т-\	sl
Всередині груп	т "j ./=1 (-1	п-т	sw
Загальна	т "і і і	п-\	s2

Наприклад, з метою виявлення впливу вмісту протеїну в ра­ціоні тварин на приріст живої ваги проведено експеримент. Було сформовано три групи молодняку свиней на відгодівлі по 5 тва­рин кожна: перша група отримувала 80 г протеїну, друга - 90, третя - 100. Середньодобовий приріст живої ваги становив, г:

1 група	430	425	440	435	440
2 група	445	450	465	460	455
3 група	470	465	480	475	460

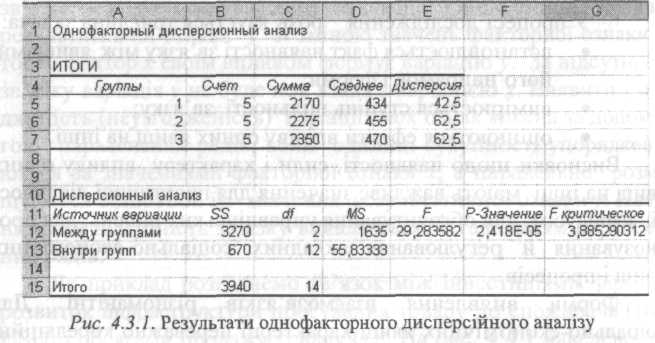
Результати дисперсійного аналізу представлено на рис. 4.3.1. В таблиці ИТОГИ подано характеристики груп: частоти (счет), сумарні і середні величини, дисперсії. Групові середні свідчать про те, що зі збільшенням вмісту протешу в раціоні се-

124

Розділ 4. Гіпотези і доведення у наукових дослідженнях

редньодобовий приріст живої ваги молодняку свиней зростає: у другій групі порівняно з першою на 21 г (455 - 434), у третій по­рівняно з другою - на 15 г (470 - 455).

В таблиці ДИСПЕРСИОННЬІЙ АНАЛИЗ наведено джерела варіації, оцінки дисперсій - міжгрупової (3270 : 2 = 1635) та внутрішньогрупової (670: 12 = 55,8). Вибіркове значення крите­рію F = 29,3 значно перевищує критичне F,_₀₀₅(2,12) - 3,88, що

дає підстави вважати розбіжності групових середніх не випадко­вими. З імовірністю 0,95 можна стверджувати, що кількість про­теїну в раціоні істотно впливає на середньодобовий приріст жи­вої маси поросят.

За принципом дисперсійного аналізу здійснюється обробка результатів складних наукових експериментів, коли вивчається вплив двох і більше факторів і шляхом оцінювання істотності розбіжностей групових середніх доводиться ефективність їхньої дії.

Отже, в усіх розглянутих прикладах результатом перевірки статистичних гіпотез є імовірнісне судження щодо значень па­раметрів однієї сукупності або істотності розбіжностей між па­раметрами різних сукупностей (груп).

125