
Основні поняття і аксіоми стереометрії та найпростіші наслідки з них
Стереометрія – це розділ геометрії, в якому вивчаються властивості просторових фігур.
Основними фігурами в просторі є точка (А, В, С,…), пряма (a, b, c,…) і площина (, β, ,…).
Способи задання точки в просторі |
Способи задання прямої в просторі |
||||||
Двома прямими, які перетинаються |
|
b
c Трьома попарно перетинаючимися площинами, якщо прямі перетину площин перетинаються |
Двома точками
|
Двома площинами, які перетинаються |
|||
Способи задання площини в просторі |
|||||||
Трьома точками, які не лежать на одній прямій |
Двома прямими, які перетинаються |
b
Двома паралельними прямими |
П
|
||||
Група аксіом, які виражають основні властивості площин у просторі
С1 |
С2 |
С3 |
Яка б не була площина, існують точки, які належать цій площині, і точки, які не належать їй.
, |
Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.
я а, |
Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.
а,b β |
Взаємне розміщення двох прямих у просторі
Прямі а і b |
|
|
|||
|
|
|
|
|
|
лежать в одній площині |
не лежать в одній площині |
|
|||
Прямі,
які не перетинаються і не лежать водній
площині, називаються мимобіжними.
Якщо одна з двох
прямих
лежить у площині,
а друга
перетинає цю
площину в точці,
яка
не лежить на першій прямій, то ці прямі
мимобіжні.
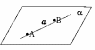
Ознака мимобіжності прямих




b
a
ab
a![]() b
b![]() b
b
Теореми існування площини |
Взаємна розміщення прямої ї площини |
1) яка проходить через дану пряму і дану точку Через пряму і точку, яка не належить їй, можна провести площину, і до того ж тільки одну.
2
А Через три точки, які не лежать на одній прямій, можна провести площину, і до того ж тільки одну.
|
Теорема про належність площині прямої, дві точки якої належать площині Якщо дві точки прямої належать площині, то вся пряма належить цій площині.
Н
А |


 Прямою
і площиною, які перетинаються
Прямою
і площиною, які перетинаються







 кщо
,
,
кщо
,
, b,
а
b,
а

 аслідок:
Площина
і пряма, яка не лежить на ній, або
аслідок:
Площина
і пряма, яка не лежить на ній, або