2.6 Система итерированных функций

Как отмечалось ранее, процедура построения фракталов представляет собой итерационный процесс – переход от одного множества к другому. На каждом шаге выполняются преобразования над множеством, полученном на предыдущем шаге. Данный алгоритм можно представить в виде следующей схемы:

(2.17)

Здесь – преобразования, выполняемые на -м шаге над множеством ( – исходное компактное множество).

На каждом шаге итерационного процесса выполняются однотипные преобразования. В общем же случае на каждом шаге могут выполняться различные преобразования, определяемые следующим образом:

. (2.18)

Преобразования вида (2.18) называются преобразованиями Хатчинсона. Преобразования Хатчинсона позволяют строить разнообразные фракталы за счет выбора элементарных преобразований .

Необходимо отметить, что если преобразования заранее определены, то получаемый результат совершенно не зависит от выбора исходного компактного множества . Кроме того, не любые преобразования Т порождают фракталы.

Если, например, преобразование Хатчинсона получено с использованием двух аффинных преобразований:

,

где

,

,

то можно построить фрактал под названием «лист» (рис. 2.15).

Рисунок 2.15 – Фрактал «лист»

Если использовать четыре аффинных преобразований вида:

,

,

,

то получим фрактал под названием «кристалл» (рис. 2.16).

Рисунок 2.16 – Фрактал «кристалл»

Задача построения предельного множества Е (аттрактора из исходного компактного множества Е_о) в результате итерационного процесса с заданным преобразованием является прямой задачей. Ее особенностью является то, что вид аттрактора определяется только коэффициентами аффинного преобразования (если такое используется) и не зависит от выбора исходного множества Е_о. В то же время можно поставить обратную задачу, а именно, определить совокупность отображений, для которых заданное множество является аттрактором. Обратная задача значительно сложнее прямой, однако имеет огромное прикладное значение, в частности, в области сжатия изображений.

Необходимость сжатия изображений обусловлена различными факторами. Основными являются:

• разгрузка каналов связи и, соответственно, снижение себестоимости передачи данных;

• экономия памяти компьютеров за счет архивации изображений и др.

2.7 Фракталы на комплексной плоскости

В системах автоматического управления процесс управления осуществляется итерационно – следующее состояние системы зависит от настоящего (и даже предыдущих):

(2.19)

Если функция управления содержит нелинейности, то процесс обычно представляется на комплексной плоскости, чтобы можно было отобразить мнимые корни уравнения n-ой степени.

Идея использования комплексных чисел вместо действительных была выдвинута Мандельбротом. Он поставил задачу пронаблюдать итерационный процесс не на прямой, а на плоскости. Процесс Мандельброта математически представляется выражением:

(2.20)

где .

Выбрав произвольное число , возведем его в квадрат и прибавим константу с для того, чтобы получить z₁. Затем повторим вычисления для того, чтобы получить и т. д.

Давайте начнем с простейшего из возможных значений константы с, а именно с = 0. Тогда при каждой итерации вычисляется точный квадрат числа: Для этой последовательности имеются три возможности:

1. При 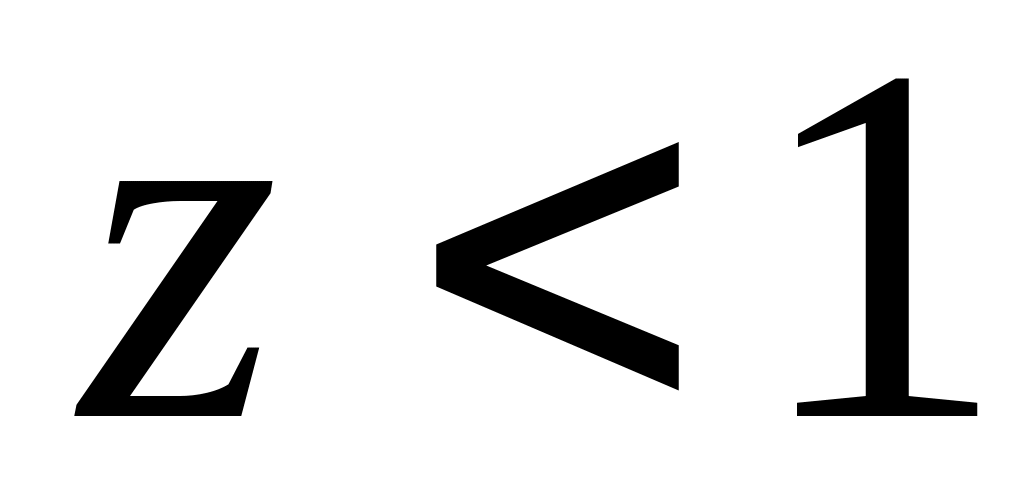числа получаются все меньшими и меньшими, их последовательность приближается к нулю. Таким образом, нуль является аттрактором этого процесса, так как все точки меньше 1 движутся к нему.

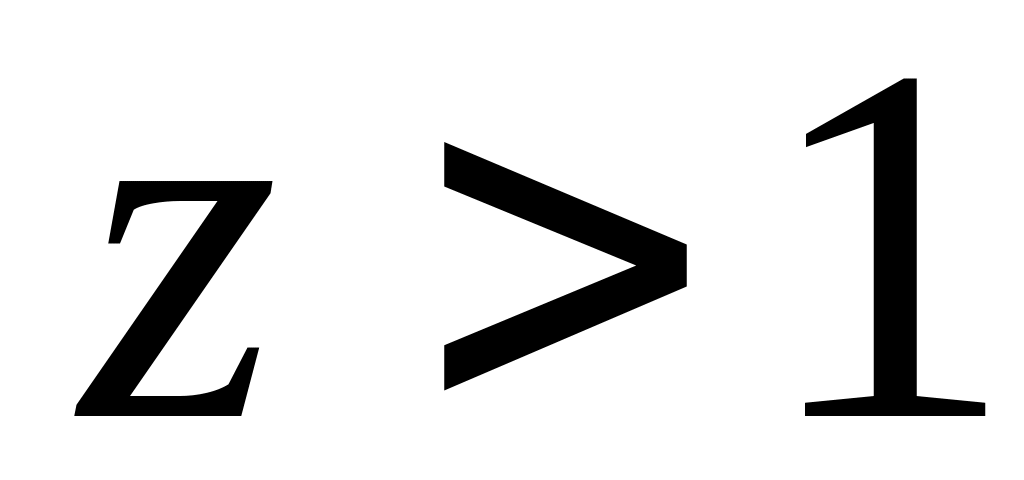2. При числа становятся все большими и большими, стремясь к бесконечности. Таким образом, для этого процесса аттрактором является бесконечность.

3. При z=1 точки находятся на расстоянии 1 от нуля. Их последовательности лежат на границе двух областей притяжения, в данном случае на окружности единичного радиуса с центром в нуле.

Ситуация ясна – плоскость делится на две зоны влияния, а границей между ними является просто окружность.

Сюрпризы начинаются, когда мы выберем ненулевое значение с, например с = - 0.12375 + 0.56508i. Здесь для последовательности z₀ — z₁ — z₂ ... также имеются три из перечисленных выше возможностей, но внутренний аттрактор уже не является нулем, а граница уже не является гладкой, то есть отличается от окружности. Эта граница показана на рисунке 2.17. Она сильно изломана, причем под лупой она выглядит так же изломанной, как и без нее.

Именно это Б. Мандельброт назвал фрактальной структурой такой границы. Она напоминает линию морского берега.

Изменяя значение с, Мандельброт получил множество точек, которые определяли границу перехода от устойчивости к хаосу (описаны в 1975 г.).

Одной из характерных особенностей этой границы является ее самоподобие. Если взглянуть на любой из ее поворотов или заливов, то можно обнаружить, что одна и та же форма встречается в различных местах и имеет разные размеры.

Множества Жюлиа (описаны в 1924 г.) строятся аналогично множеству Мандельброта, только величина c задается постоянной. Процесс итерационных вычислений для каждой точки продолжается до тех пор, пока z_n+1=z_n²+с не уйдёт из круга радиусом 2. Представленное на рисунке 2.18 множество получается при с=-0,20+0,75i.

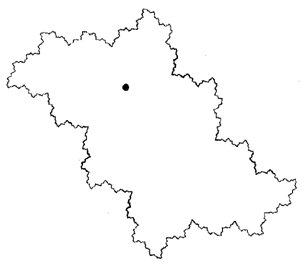
Рисунок 2.17 – Бассейн с одной притягивающей точкой

Здесь множество Жюлиа представляет собой не единственную деформированную окружность, а состоит из бесконечного числа деформированных окружностей, образующих, однако, связное множество. Внутренние точки этого множества притягиваются не одной неподвижной точке, а к множеству точек.

Рисунок 2.18 –Заполняющее множество Жюлиа для z²-0,20+0,75i

Ясно, что величина с будет определять вид множества Жюлиа. Правило, по которому множество Жюлиа будет принимать тот или иной вид, определяет граница множества Мандельброта М. Оно представлено на рисунке 2.19 как закрашенная черным цветом часть комплексной с-плоскости.

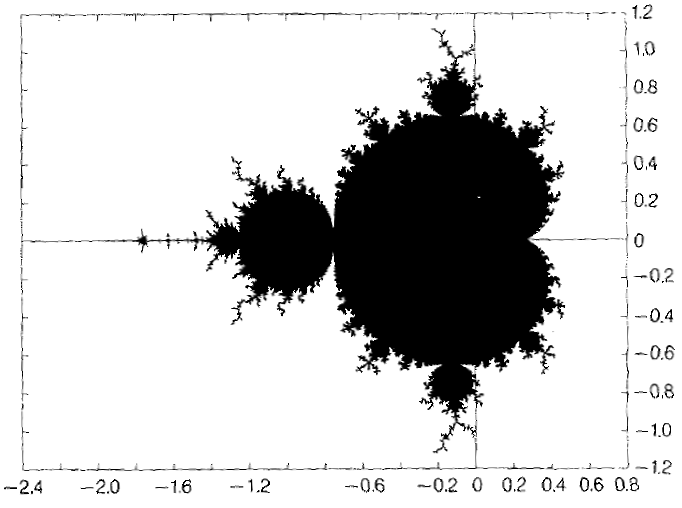
Рисунок 2.19 – Вид границы множества Мандельброта на комплексной плоскости

На рисунке 2.20 показаны изменения вида множества Жюлиа в различных граничных точках множества М.

Каждое комплексное число с либо принадлежит черной структуре М, либо нет. Соответствующие множества Жюлиа процесса х → х² + с существенно различаются. Они представляют собой связные структуры, когда с лежит внутри М, и рассыпаются на бесконечное число кусочков, когда с лежит снаружи.

Представим себе некоторый путь в с-плоскости, начинающийся внутри М и заканчивающийся вне его. Если менять с, двигаясь вдоль этого пути, то качественные изменения происходят с соответствующими множествами Жюлиа тогда, когда с пересекает границу М: они, как будто взорвавшись, превращаются в облако из бесконечного числа точек. В этом смысле граница множества М определяет момент математического фазового перехода для множеств Жюлиа отображения х → х² + іс.

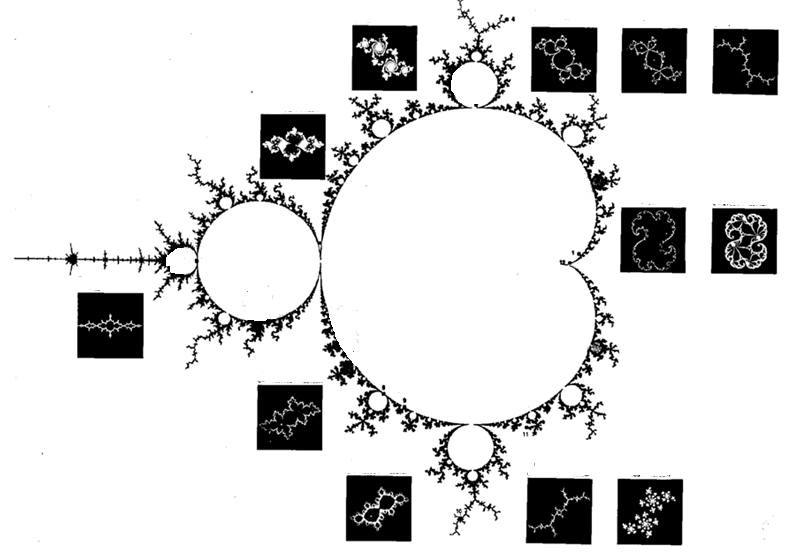
Рисунок 2.20 – Изменения вид множества Жюлиа по границе множества Мандельброта