4.2 От аналитичности к гладкости функций

Рассмотрим некоторую дифференцируемую функцию и разложим ее ряд Тейлора в окрестности некоторой точки :

(4.11)

По традиции представление этим рядом считается полезным только в том случае, если он сходится в некоторой окрестности и сумма его равна . В этом случае f(x) называют аналитической в точке х₀.

Ряд можно дифференцировать в некоторой (возможно) меньшей окрестности и его коэффициенты равны:

, (4.12)

где .

Для дальнейшего анализа нам потребуется ввести некоторые определения и обозначения.

Определения:

1. Отображение является дифференцируемым класса , если каждая из функций является раз дифференцируемой;

2. Отображение называется аналитическим, если каждая из функций является аналитической, то есть может быть разложена в сходящийся ряд Тейлора;

3. Отображение называется гладким (или бесконечно дифференцируемым), если для всякого неотрицательного целого отображение является дифференцируемым.

Рассмотрим теперь функцию . Данная функция является аналитической, и ее ряд Тейлора имеет вид:

. (4.13)

На рисунке 4.3 показаны графики полиномиальных функций, которые получаются, если ограничиться первыми членами .

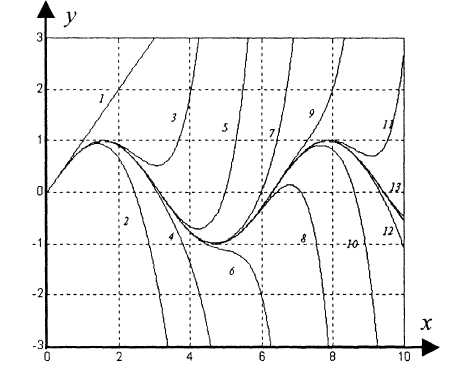
Рисунок 4.3 – Усечение ряда Тейлора для аналитической функции (цифры определяют число членов разложения)

Из рисунка 4.3 отчетливо видна сходимость ряда Тейлора. Однако замечаем, что даже при очень большом числе членов разложения приближение ухудшается с удалением от начала координат. С другой стороны, вблизи начала координат приближение очень хорошее. С увеличением числа членов разложения интервал, на котором точность приближения улучшается, также растёт. Это принципиальное отличие aнaлитических функций от другого класса функций, а именно гладких функций.

Для гладких функций ряд Тейлора может расходиться или сходиться, но не к той сумме.

Рассмотрим пример.

Пусть задана функция:

(4.14)

Данная функция имеет следующий вид (рис. 4.4).

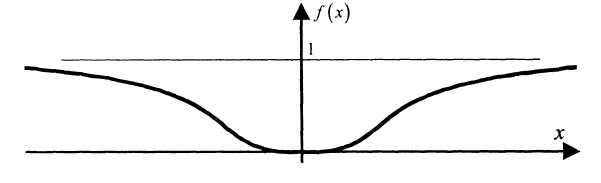
Рисунок 4.4 – Гладкая функция

Легко проверить, что для любого :

.

Действительно, например, для имеем:

.

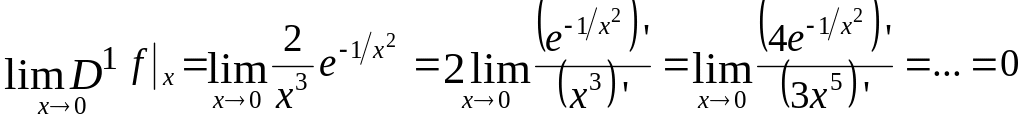Таким образом, для любого , ряд Тейлора вблизи начала координат имеет вид

0 + 0х² +0х³+ …

Этот ряд, конечно, сходится, но не к , а к , то есть является гладкой, но не аналитической функцией.

Однако из этого не следует, что гладкие функции не могут использоваться для приближений. Как остроумно заметил один из теоретиков теории катастроф Зиман, пора, когда сходимость остаточного члена при являлась основным инструментом приближений и когда «было дозволено, чтобы «хвост» ряда Тейлора вилял собакой», явно прошла. Так, например, ряд Тейлора хотя и не сходится к , хорошо приближает эту функцию в начале координат с качественной точки зрения. Он чётко улавливает, что очень плоская в нуле. Чего он не улавливает, так это то, что начало есть локальный минимум для .

Для любой гладкой функции определим ряд Тейлора в начале как формальный ряд:

. (4.15)

Ограничиваясь членами степени не выше , получаем -струю.

Определение.

-струей гладкой функции в точке х₀ (обозначение ) назовем усеченный ряд Тейлора данной функции в окрестности точки х₀, то есть:

. (4.16)

Если ввести замену переменных у = х–х₀ и перейти от функции f(x) к функции , то есть:

,

то получим:

. (4.17)

Поэтому без снижения общности точку х₀ можно принять за начало координат и в дальнейшем считать, если нет особой оговорки, что х₀ = 0, а формулу (4.17) запишем в следующем виде (индекс “0” у опущен):

. (4.18)

Обозначение для -струи взято по первой букве английского слова «jet» – «струя».

Усеченный ряд Тейлора (4.18) представляет собой многочлен, задающий полиномиальные функции независимо от того, сходится или нет ряд Тейлора.

Уместно напомнить некоторые определения.

Определение 1. Степенью одночлена называется сумма степеней всех переменных, входящих в данный одночлен.

Например: – многочлен 26-й степени.

Определение 2. Степенью многочлена (полинома) р(х) называется наивысшая из степеней одночленов, входящих в данный многочлен.

Определение 3. Порядком многочлена (полинома) р(х) называется наименьшая из степеней одночленов, входящих в данный многочлен.

Определение 4. Функция имеет в начале координат (то есть в точке ) порядок , если:

. (4.19)

Если многочлен степени , то многочлен имеет порядок . Другими словами, -е производные в нуле для и f(x) совпадают для .

Благодаря этому ряд Тейлора и его усечение в виде -струи оказывается удобным формальным средством для получения информации о производных функции и, значит, о ее форме вблизи начала координат, то есть при х₀ = 0.