
- •Теория с примерами (кратко)
- •Параметры оцкп
- •Типовая задача
- •Экспериментальные данные для оцкп
- •Уровни и интервалы варьирования факторов
- •3.1. Выполним предварительную обработку экспериментальных данных опытов (результаты расчётов внесены в таблицу 5):
- •4.3. Проверим полученное двухфакторное ортогонализированное уравнение регрессии второго порядка на адекватность по критерию Фишера (результаты расчета внесены в таблицу 6):
- •5. Проведем оптимизацию изучаемой технической системы.
Задача 5 +
Многофакторное ортогонализированное уравнение регрессии второго порядка. Ортогональный центральный композиционный план (ОЦКП)
Теория с примерами (кратко)
1.
Многофакторное
ортогонализированное
уравнение регрессии второго
порядка для
![]() – факторов
имеет вид
– факторов
имеет вид
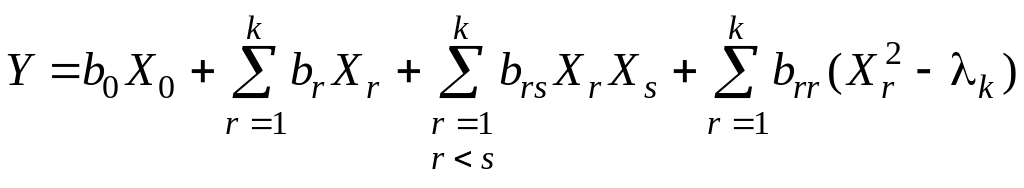 ,
,
![]() . (1)
. (1)
Моделирование
технической системы, описываемой
стохастическими закономерностями,
лучше всего проводить в ортогональных
факторах. Это даёт целый ряд преимуществ,
таких как независимое определение
коэффициентов уравнения регрессии и
их дисперсий значимости, позволяет
достаточно просто рассчитать абсолютную
погрешность прогнозирования параметра
![]() ,
а также облегчает интерпретацию
полученных результатов. Факторы
,
а также облегчает интерпретацию
полученных результатов. Факторы
![]() в уравнении (1), как будет показано
ниже, ортогональны.
в уравнении (1), как будет показано
ниже, ортогональны.
2.
Для построения многофакторного
ортогонализированного
уравнения регрессии второго
порядка будем использовать ортогональный
центральный композиционный план (ОЦКП),
который состоит из полного факторного
плана (ПФП), одного опыта в центре плана
(0, 0, …, 0) и 2k звёздных
точек
![]() ,
… ,
,
… ,
![]() (по 2 звёздные точки на каждый фактор).
(по 2 звёздные точки на каждый фактор).
Количество
опытов число опытов ПФП, в котором каждый
![]() ,
равно
,
равно
![]() , (2)
, (2)
Количество опытов ОЦКП
![]() . (3)
. (3)
2.1. Звёздное плечо
![]() и ортогонализирующий
коэффициент
и ортогонализирующий
коэффициент
![]() для ОЦКП равны
для ОЦКП равны
![]() ; (4)
; (4)
![]() . (5)
. (5)
2.2.
Параметры ОЦКП для
![]() приведены в таблице 1.
приведены в таблице 1.
Таблица 1
Параметры оцкп
Параметры |
Число факторов k |
||||||
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
4 |
8 |
16 |
32 |
64 |
128 |
256 |
|
4 |
6 |
8 |
10 |
12 |
14 |
16 |
|
9 |
15 |
25 |
43 |
77 |
143 |
273 |
|
1.0000 |
1.2154 |
1.4142 |
1.5960 |
1.7606 |
1.9095 |
2.0449 |
|
0.6667 |
0.7303 |
0.8000 |
0.8627 |
0.9117 |
0.9461 |
0.9684 |
|
0.3333 |
0.2697 |
0.2000 |
0.1373 |
0.0883 |
0.0539 |
0.0316 |
|
0.3333 |
0.7469 |
1.2000 |
1.6846 |
2.1882 |
2.7000 |
3.2133 |
|
9 |
15 |
25 |
43 |
77 |
143 |
273 |
|
6.000 |
10.954 |
20.000 |
37.094 |
70.200 |
135.292 |
264.363 |
|
4 |
8 |
16 |
32 |
64 |
128 |
256 |
|
2.000 |
4.364 |
8.000 |
12.977 |
19.218 |
26.589 |
34.973 |
3.
Матрица планирования (МП) для
построения многофакторного
ортогонализированного
уравнения регрессии второго
порядка для
факторов состоит из
![]() опытов с
опытов с
![]() дублями
в каждом опыте. МП
строится на
базе ОЦКП и включает в себя следующие
столбцы:
дублями
в каждом опыте. МП
строится на
базе ОЦКП и включает в себя следующие
столбцы:
![]() .
Значения
.
Значения
![]() позволяют провести предварительную
обработку экспериментальных данных
(расчёт выборочных средних
позволяют провести предварительную
обработку экспериментальных данных
(расчёт выборочных средних
![]() и дисперсий
и дисперсий
![]() в каждом опыте, проверку всех выборочных
дисперсий на однородность по критерию
Кохрена, расчёт дисперсии воспроизводимости
в каждом опыте, проверку всех выборочных
дисперсий на однородность по критерию
Кохрена, расчёт дисперсии воспроизводимости
![]() и её числа степеней свободы
и её числа степеней свободы
![]() ).
).
Для
построения МП
должны быть заданы диапазоны варьирования
факторов:
![]()
![]() .
Взаимосвязь
нормированных
.
Взаимосвязь
нормированных
![]() и натуральных
и натуральных
![]()
![]() значений факторов задаётся следующими
уравнениями:
значений факторов задаётся следующими
уравнениями:
![]() ,
,
![]() (6)
(6)
![]() ,
(7)
,
(7)
![]() ,
(8)
,
(8)
![]() ,
(9)
,
(9)
где
![]() – основной
уровень, интервал варьирования,
максимальное и минимальное натуральные
значения факторов хr,
соответственно. Из уравнений (6) – (9)
следует, что если
,
то
– основной
уровень, интервал варьирования,
максимальное и минимальное натуральные
значения факторов хr,
соответственно. Из уравнений (6) – (9)
следует, что если
,
то
![]() для всех
для всех
![]() .
Значения
фиктивного фактора
.
Значения
фиктивного фактора
![]() равны
равны
![]() для всех
для всех
![]() .
.
4. Предварительная
обработка экспериментальных данных МП
с числом опытов
![]() и n
дублей
и n
дублей
![]() в каждом опыте, включает в себя расчёт
выборочных средних
и выборочных дисперсий
в каждом опыте, проверку выборочных
дисперсий на однородность по критерию
Кохрена, расчёт дисперсии воспроизводимости
и её числа степеней свободы
.
Указанные процедуры выполняются по
уравнениям (10) – (16).
в каждом опыте, включает в себя расчёт
выборочных средних
и выборочных дисперсий
в каждом опыте, проверку выборочных
дисперсий на однородность по критерию
Кохрена, расчёт дисперсии воспроизводимости
и её числа степеней свободы
.
Указанные процедуры выполняются по
уравнениям (10) – (16).
4.1. Выборочные параметры:
‑ выборочное среднее в каждом опыте
 ,
; (10)
,
; (10)
‑ выборочная дисперсия в каждом опыте
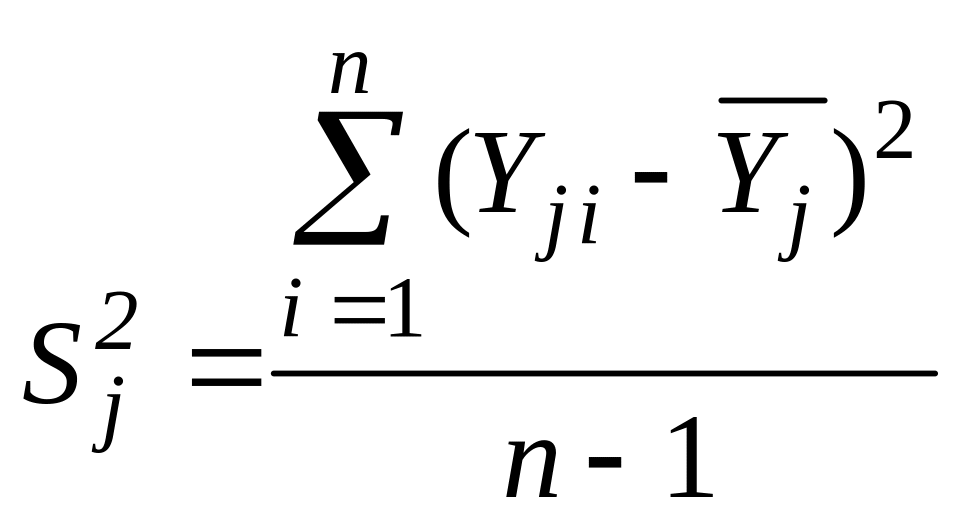 ,
. (11)
,
. (11)
4.2. Проверка всех
выборочных дисперсий на однородность.
Так как объём всех выборок одинаковый
![]() ,
то проверку дисперсий на однородность
можно провести по критерию Кохрена:
,
то проверку дисперсий на однородность
можно провести по критерию Кохрена:
‑ экспериментальное значение критерия Кохрена
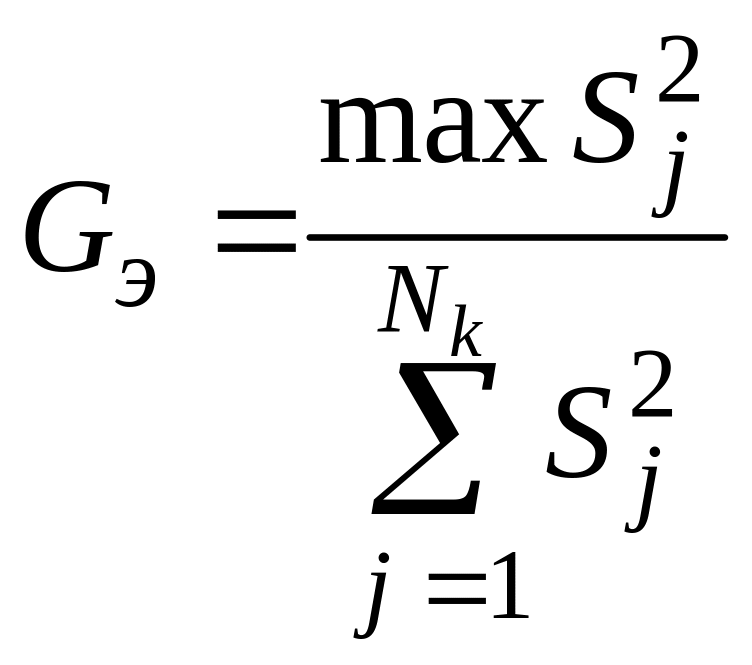 ; (12)
; (12)
‑ табличное
значение критерия Кохрена
![]() при числах степеней свободы
при числах степеней свободы
![]() ,
,
![]() и доверительной вероятности
и доверительной вероятности
![]() выбирается из таблицы приложения 5;
выбирается из таблицы приложения 5;
‑ выборочные
дисперсии
![]() с вероятностью не менее 95 % однородны,
если
с вероятностью не менее 95 % однородны,
если
![]() ; (13)
; (13)
‑ выборочные дисперсии неоднородны, если
![]() . (14)
. (14)
Если выборочные дисперсии неоднородны, то дальнейшее моделирование изучаемой технической системы предложенным математическим аппаратом некорректно. Необходимо переделать опыт, в котором выборочная дисперсия наибольшая.
4.3. Если
число дублей
![]() ,
то случайные значения каждого опыта
следует проверить на промах по критерию
Смирнова – Граббса, а также на
принадлежность их к нормальному закону
распределения по критерию среднего
абсолютного отклонения. В случае
обнаружения промаха или отклонения
экспериментальных данных от нормального
закона распределения в каком-либо опыте,
последний необходимо переделать. Если
число дублей
,
то случайные значения каждого опыта
следует проверить на промах по критерию
Смирнова – Граббса, а также на
принадлежность их к нормальному закону
распределения по критерию среднего
абсолютного отклонения. В случае
обнаружения промаха или отклонения
экспериментальных данных от нормального
закона распределения в каком-либо опыте,
последний необходимо переделать. Если
число дублей
![]() ,
то проверку случайных значений выборки
на промах и на принадлежность их к
нормальному закону распределения можно
не проводить.
,
то проверку случайных значений выборки
на промах и на принадлежность их к
нормальному закону распределения можно
не проводить.
4.4. Если все выборочные дисперсии однородны, то дисперсия воспроизводимости и её число степеней свободы рассчитывают следующим образом:
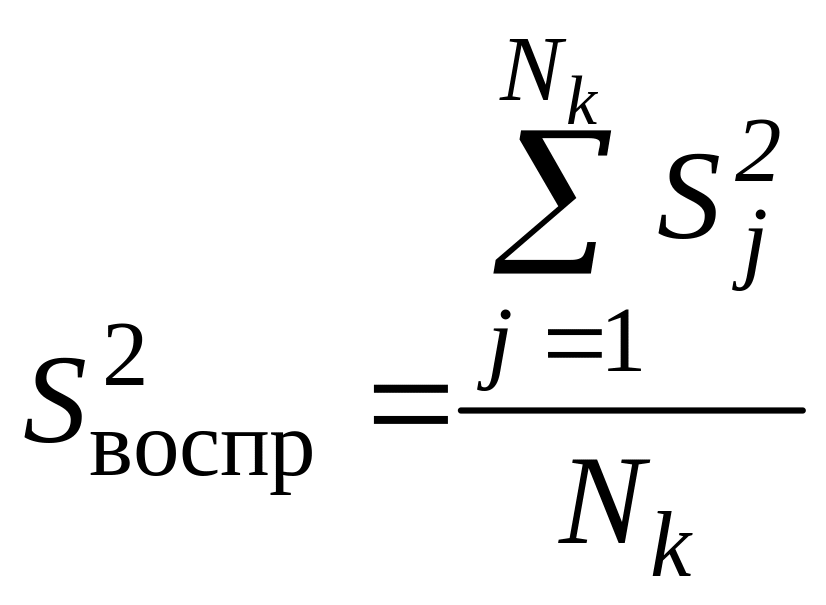 ; (15)
; (15)
![]() . (16)
. (16)
5.
Матрица моделирования (ММ) для
построения
многофакторного ортогонализированного
уравнения
регрессии
второго порядка
состоит
из
опытов
и
дублей
в каждом
опыте,
включает в себя следующие столбцы:
![]() ,
,
![]()
![]() ,
значения которых служат для окончательной
обработки экспериментальных данных
(расчёт
коэффициентов уравнения регрессии
,
значения которых служат для окончательной
обработки экспериментальных данных
(расчёт
коэффициентов уравнения регрессии
![]() ,
проверка их на значимость по критерию
Стьюдента, а само уравнение регрессии
на адекватность по критерию Фишера,
расчёт абсолютной погрешности
прогнозирования параметра
в случае адекватности уравнения
регрессии).
,
проверка их на значимость по критерию
Стьюдента, а само уравнение регрессии
на адекватность по критерию Фишера,
расчёт абсолютной погрешности
прогнозирования параметра
в случае адекватности уравнения
регрессии).
Покажем,
что
![]() взаимно ортогональны.
взаимно ортогональны.
Определение.
Факторы
![]() ортогональны, если
ортогональны, если
![]() .
.
Из таблицы 2 следует, что
![]() ,
(
,
(![]() );
);
![]() ;
;
ортогональность остальных факторов по данным таблицы 2 проверить самостоятельно.
Таблица 2
ММ для построения двухфакторного ортогонализированного
уравнения регрессии второго порядка на базе ОЦКП
|
|
|
|
|
|
|
|
|
|
1 |
+ |
– |
– |
+ |
1/3 |
1/3 |
|
|
|
2 |
+ |
+ |
– |
– |
1/3 |
1/3 |
|
|
|
3 |
+ |
– |
+ |
– |
1/3 |
1/3 |
|
|
|
4 |
+ |
+ |
+ |
+ |
1/3 |
1/3 |
|
|
|
5 |
+ |
0 |
0 |
0 |
‑ 2/3 |
‑ 2/3 |
|
|
|
6 |
+ |
– |
0 |
0 |
1/3 |
‑ 2/3 |
|
|
|
7 |
+ |
+ |
0 |
0 |
1/3 |
‑ 2/3 |
|
|
|
8 |
+ |
0 |
– |
0 |
‑ 2/3 |
1/3 |
|
|
|
9 |
+ |
0 |
+ |
0 |
‑ 2/3 |
1/3 |
|
|
|
|
9 |
6 |
6 |
4 |
2 |
2 |
|
|
|
6. Коэффициенты многофакторного ортогонализированного уравнения регрессии второго порядка для ММ на базе ОЦКП для ортогональных факторов рассчитывают по формулам:
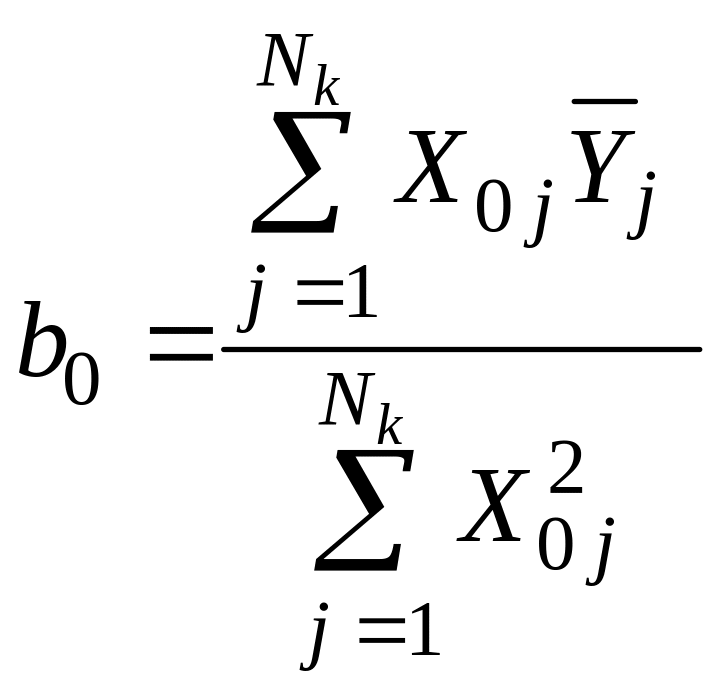 ; (17)
; (17)
 ,
,
![]() ; (18)
; (18)
 ,
,
![]() ; (19)
; (19)
 ,
. (20)
,
. (20)
6.1.
Значения
![]() ,
,
![]() ,
,
 ,
,
![]() ,
необходимые для определения
по уравнениям (17) – (20), для ММ на
базе ОЦКП рассчитывают по уравнениям,
приведённым в таблице 1.
,
необходимые для определения
по уравнениям (17) – (20), для ММ на
базе ОЦКП рассчитывают по уравнениям,
приведённым в таблице 1.
Значения
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
необходимые для определения
по уравнениям (17) – (20), рассчитывают
по суммам соответствующих столбцов ММ.
,
необходимые для определения
по уравнениям (17) – (20), рассчитывают
по суммам соответствующих столбцов ММ.
6.2. Дисперсии значимости коэффициентов многофакторного ортогонализированного уравнения регрессии второго порядка для ММ на базе ОЦКП для ортогональных факторов рассчитывают по формулам
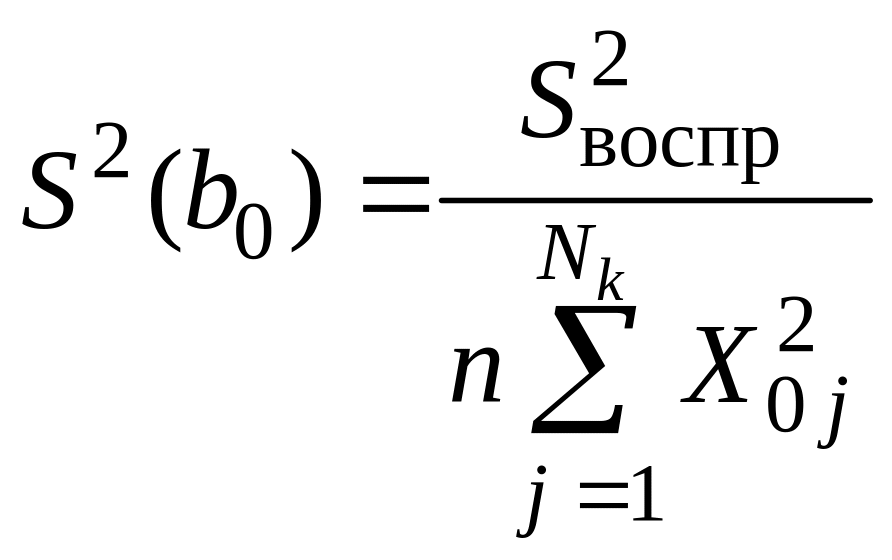 ; (21)
; (21)
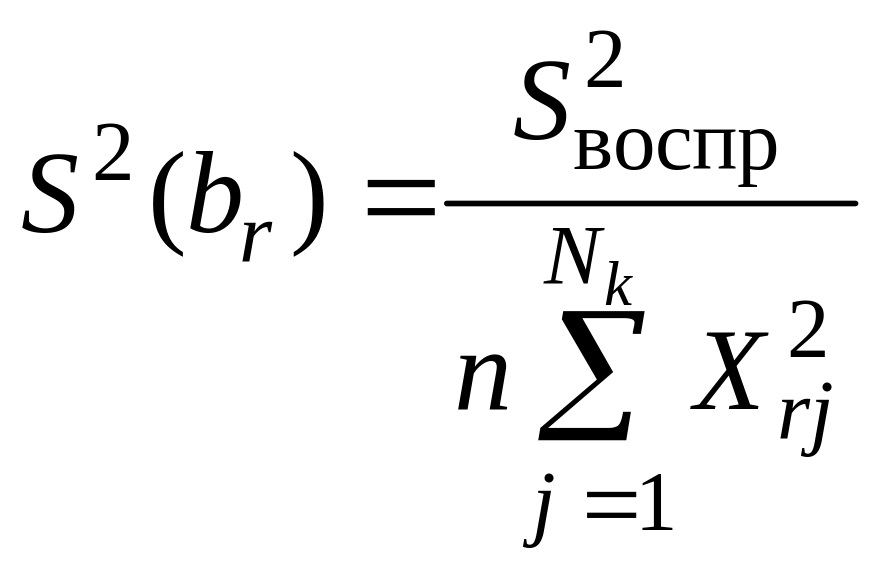 ,
,
![]() ; (22)
; (22)
 ,
,
![]() ; (23)
; (23)
 ,
. (24)
,
. (24)
Важным свойством ММ на базе ОЦКП является равенство дисперсий значимости
![]() ,
; (25)
,
; (25)
![]() ,
; (26)
,
; (26)
![]() ,
. (27)
,
. (27)
6.3. Доверительные интервалы коэффициентов многофакторного ортогонализированного уравнения регрессии второго порядка рассчитывают по формулам
![]() ; (28)
; (28)
![]() ,
; (29)
,
; (29)
![]() ,
; (30)
,
; (30)
![]() ,
; (31)
,
; (31)
где
![]() – табличное
значение критерия Стьюдента при числе
степеней свободы
– табличное
значение критерия Стьюдента при числе
степеней свободы
![]() и доверительной вероятности
выбирается из таблицы приложения 2.
и доверительной вероятности
выбирается из таблицы приложения 2.
Важным свойством ММ на базе ОЦКП является равенство доверительных интервалов
![]() ,
; (32)
,
; (32)
![]() ,
,
![]() ; (33)
; (33)
![]() ,
. (34)
,
. (34)
Коэффициенты многофакторного ортогонализированного уравнения регрессии второго порядка значимы, если
![]() ; (35)
; (35)
![]() ,
; (36)
,
; (36)
![]() ,
; (37)
,
; (37)
![]() ,
. (38)
,
. (38)
Если для какого-либо регрессионного коэффициента указанное неравенство не выполняется, то этот коэффициент незначим, и он исключается из полученного уравнения регрессии.
7. Дисперсию
адекватности
![]() и её число степеней свободы
и её число степеней свободы
![]() многофакторного
ортогонализированного
уравнения регрессии второго
порядка рассчитывают по формулам
многофакторного
ортогонализированного
уравнения регрессии второго
порядка рассчитывают по формулам
![]() ; (39)
; (39)
![]() ; (40)
; (40)
![]() ; (41)
; (41)
где
![]() – остаточная
сумма квадратов;
– число
опытов;
– число
дублей в каждом опыте;
– остаточная
сумма квадратов;
– число
опытов;
– число
дублей в каждом опыте;
![]() – значение
параметра Y,
рассчитанное по многофакторному
ортогонализированному
уравнению регрессии второго
порядка
– значение
параметра Y,
рассчитанное по многофакторному
ортогонализированному
уравнению регрессии второго
порядка
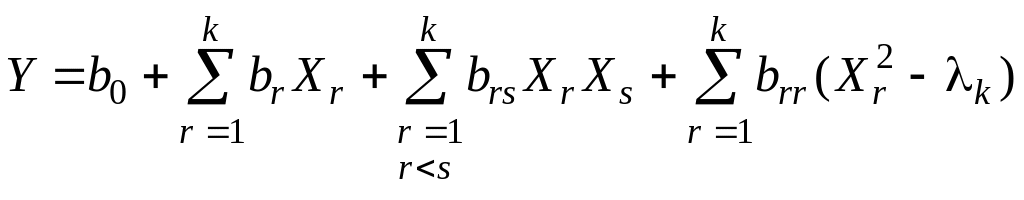 ,
,
в
котором оставлены только значимые
коэффициенты уравнения регрессии;
![]() – число
значимых коэффициентов многофакторного
ортогонализированного
уравнения регрессии второго
порядка.
– число
значимых коэффициентов многофакторного
ортогонализированного
уравнения регрессии второго
порядка.
8.
Проверка многофакторного
ортогонализированного
уравнения
регрессии любого
порядка
на адекватность производится по критерию
Фишера. В процессе построения уравнения
регрессии определяются дисперсия
воспроизводимости, дисперсия адекватности
и их числа степеней свободы:
![]() .
Проверка уравнения регрессии любого
порядка
на адекватность сводится к проверке
дисперсий
.
Проверка уравнения регрессии любого
порядка
на адекватность сводится к проверке
дисперсий
![]() на однородность по критерию Фишера:
на однородность по критерию Фишера:
‑ экспериментальное
значение критерия Фишера
![]() (отношение бльшей
дисперсии к мньшей)
(отношение бльшей
дисперсии к мньшей)
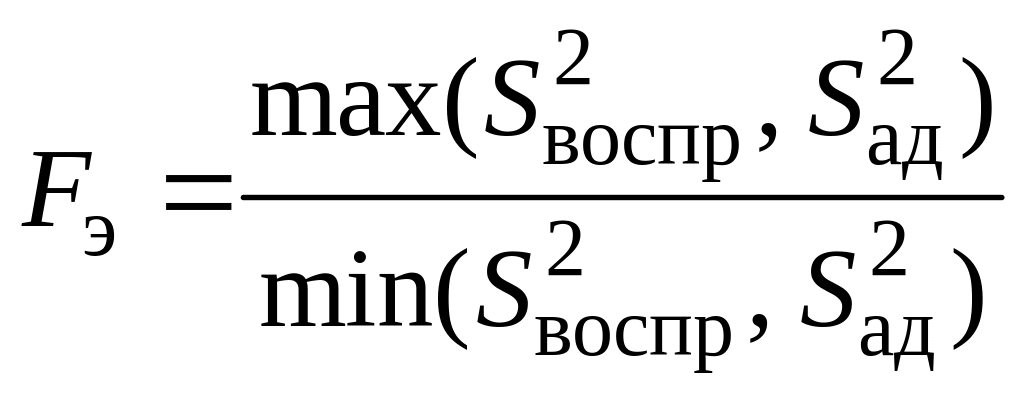 ; (42)
; (42)
‑ табличное
значение критерия Фишера
![]() ,
в котором на первом месте стоит число
степени свободы бльшей
дисперсии
,
в котором на первом месте стоит число
степени свободы бльшей
дисперсии
![]() ,
а на втором – число
степени свободы мньшей
дисперсии
,
а на втором – число
степени свободы мньшей
дисперсии
![]() ,
при доверительной вероятности
и выбирается
из таблицы приложения 4;
,
при доверительной вероятности
и выбирается
из таблицы приложения 4;
‑ величины и определяются следующим образом:
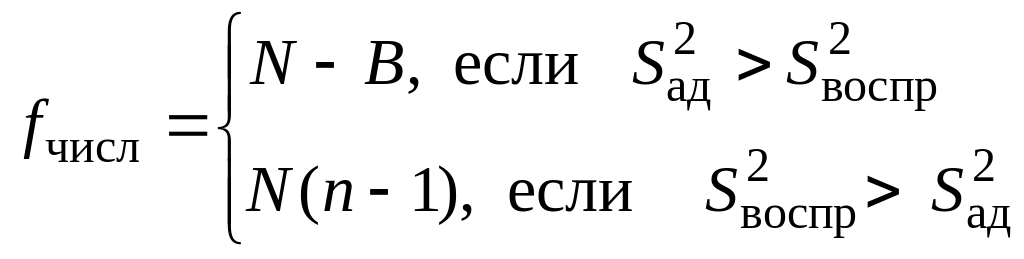 ; (43)
; (43)
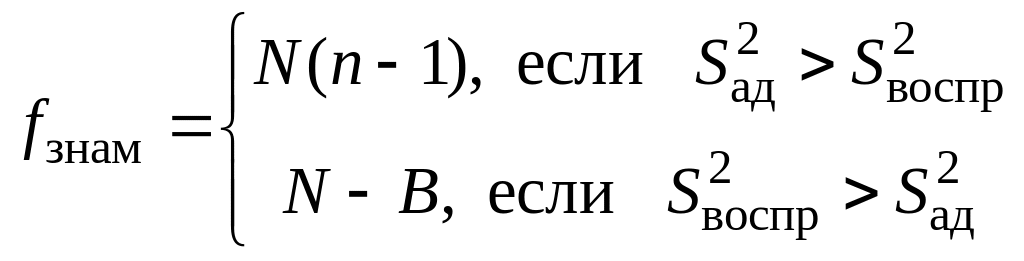 ; (44)
; (44)
‑ многофакторное ортогонализированное уравнение регрессии любого порядка с доверительной вероятностью не менее 95 % адекватно, если
![]() ; (45)
; (45)
‑ многофакторное ортогонализированное уравнение регрессии любого порядка неадекватно, если
![]() . (46)
. (46)
9. Предельную
абсолютную погрешность
![]() параметра
параметра
![]() ,
рассчитанного по многофакторному
ортогонализированному
уравнению регрессии второго
порядка
,
при условии, что все факторы ортогональны,
определяют по формуле
,
рассчитанного по многофакторному
ортогонализированному
уравнению регрессии второго
порядка
,
при условии, что все факторы ортогональны,
определяют по формуле
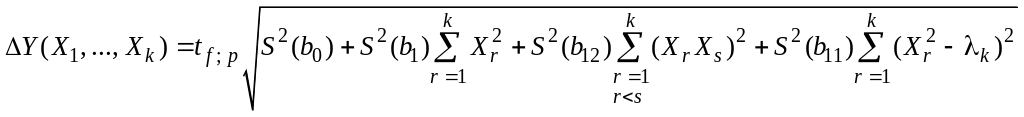 ,
(47)
,
(47)
где – табличное значение критерия Стьюдента при числе степеней свободы и доверительной вероятности выбирают из таблицы приложения 2.
10. Если многофакторное
ортогонализированное
уравнение регрессии второго
порядка, в котором оставлены только
значимые коэффициенты уравнения
регрессии
 ,
адекватно
и все коэффициенты при квадратичных
членах одного знака, то при
,
адекватно
и все коэффициенты при квадратичных
членах одного знака, то при
![]() уравнение регрессии имеет абсолютный
максимум, а при
уравнение регрессии имеет абсолютный
максимум, а при
![]() – минимум.
– минимум.
![]() ,
где
,
где
![]() – оптимальные
значения факторов, являющиеся корнями
системы уравнений:
– оптимальные
значения факторов, являющиеся корнями
системы уравнений:
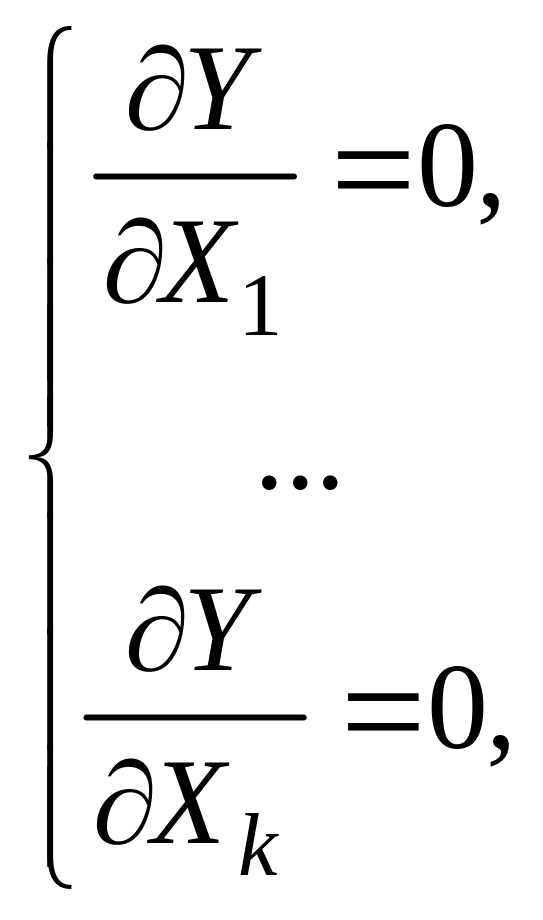 (48)
(48)
или
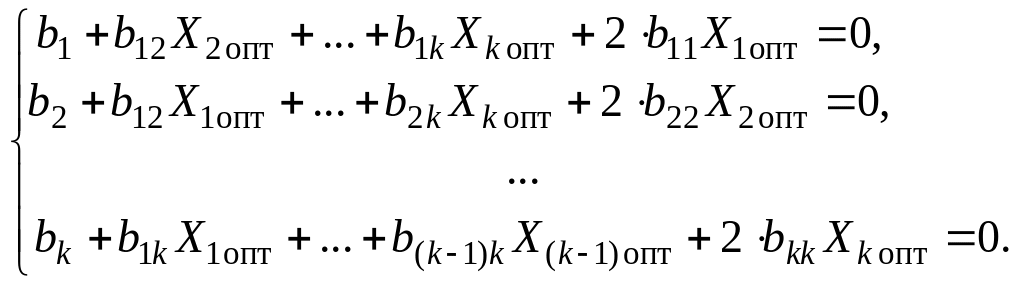 (49)
(49)
Соответствующие
натуральные значения факторов![]() рассчитывают по уравнениям (7) – (10)
рассчитывают по уравнениям (7) – (10)
![]() ,
. (50)
,
. (50)
Максимум (минимум)
параметра
![]() и его предельную
абсолютную погрешность
и его предельную
абсолютную погрешность
![]() рассчитывают по уравнениям (1) и (47)
рассчитывают по уравнениям (1) и (47)
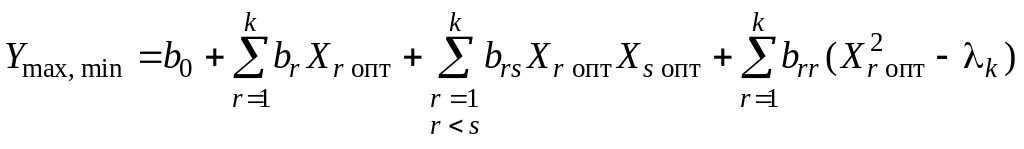 ; (51)
; (51)
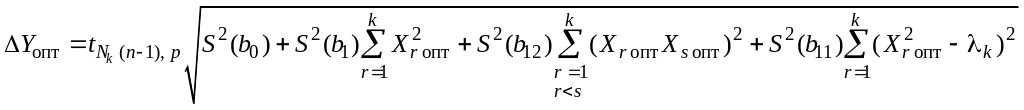 .(52)
.(52)
Если все смешанные
коэффициенты
![]() незначимы, то система уравнений (48)
приобретает диагональный вид и оптимальные
значения факторов можно рассчитать по
формулам
незначимы, то система уравнений (48)
приобретает диагональный вид и оптимальные
значения факторов можно рассчитать по
формулам
![]() ,
. (53)
,
. (53)
