БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Приборостроительный факультет

Кафедра экспериментальной и теоретической физики

ИЗУЧЕНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

Методическое указание к лабораторной работе №1

по дисциплине «Общая физика»

раздел «Механика. Молекулярная физика»

Минск 2011 г.

Введение

Физические законы устанавливаются и проверяются путем накопления и количественного сопоставления изменений экспериментальных данных, характеризующих изучаемое физическое явление. Таким образом, физика - это количественная наука, устанавливающая физические закономерности, которые выражаются в виде математических формул, связывающих между собой числовые значения физических параметров. Практически такая же методика измерений используется и в инженерных исследованиях и испытаниях. Поэтому целью физического практикума является выработка навыков правильного проведения измерений числовых значений различных физических параметров и умения оценивать погрешности и сопоставлять полученные данные с математическими формулами.

I Физические измерения и погрешности

Прежде всего, поясним, что вообще понимается под измерением. Измерением называется сравнение интересующей нас физической величины с соответствующим эталоном или измерительным прибором, проградуированным по эталону. По характеру проведения измерений их делят на прямые и косвенные. Под прямыми измерениями понимают такие измерения, при котором в ходе опыта непосредственно измеряется интересующая нас величина. Однако далеко не все величины можно определить путем прямого измерения. Например, плотность тела, определить непосредственным измерением весьма затруднительно. Но известно, что известно, что плотность определяется по формуле

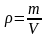(1)

где m и - V масса и объем,. Измерение массы тела и его объема уже не представляет существенных трудностей, поэтому, измерив на опыте величины m и V, мы можем подставить их в (1) и рассчитать интересующее нас значение ρ. Такие измерения, при которых интересующая нас величина не измеряется непосредственно, а рассчитывается по некоторой формуле, на основе результатов прямых измерений, называются косвенными измерениями.

2 Абсолютная и относительная погрешности измерений

Истинное значение физической величины определить абсолютно точно практически невозможно, т.к. любая операция измерения связана с рядом ошибок или, иначе, погрешностей. Причины погрешностей могут быть самыми различными. Их возникновение может быть связано с неточностями изготовления и регулировки измерительного прибора, обусловлено физическими особенностями исследуемого объекта (например, при измерении диаметра проволоки неоднородной толщины результат случайным образом зависит от выбора участка измерений), причинами случайного характера и т.д.

Задача экспериментатора заключается в том, чтобы уменьшить их влияние на результат, а также указать, насколько полученный результат близок к истинному.

Существуют понятия абсолютной и относительной погрешности.

Под абсолютной погрешностью измерений будет понимать разницу между результатом измерения и истинным значением измеряемой величины:

∆x_i=x_i-x_и (2)

где ∆x_i – абсолютная погрешность i-го измерения, x_i_- результат i-го измерения, x_и – истинное значение измеряемой величины.

Результат любого физического измерения принято записывать в виде:

x =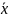 ± 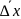(3)

где – среднее арифметическое значение измеряемой величины, наиболее близкое к истинному значению ( справедливость x_и≈ будет показана ниже), - абсолютная ошибка измерений.

Равенство (3) следует понимать таким образом, что истинное значение измеряемой величины лежит в интервале [ - , + ].

Абсолютная погрешность – величина размерная, она имеет ту же размерность, что и измеряемая величина.

Абсолютная погрешность не полностью характеризует точность произведенных измерений. В самом деле, если мы измерим с одной и той же абсолютной ошибкой ± 1 мм отрезки длиной 1 м и 5 мм, точность измерений будут несравнимы. Поэтому, наряду с абсолютной погрешностью измерения вычисляется относительная погрешность.

Относительной погрешностью измерений называется отношение абсолютной погрешности к самой измеряемой величине:

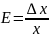(4)

Относительная погрешность – величина безразмерная. Она выражается в процентах:

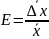100 (5)

В приведенном выше примере относительные ошибки равны 0,1 и 20. Они заметно различаются между собой, хотя абсолютные значения одинаковы. Относительная ошибка дает информацию о точности