Лекция 26. Переходные процессы в нэц

ВВЕДЕНИЕ

Методы анализа переходных процессов в НЭЦ разделяются на графические и аналитические. Под графическим (графо-аналитическими) понимают методы, в которых основными операциями по определению искомых токов или напряжений являются графические построения. (Например, метод графического интегрирования.)

Аналитическими называют методы, в которых используется аппроксимация ВАХ НЭ и точное или приближенное решение дифференциальных уравнений цепи (например, метод кусочно-линейной аппроксимации, метод интегрируемой нелинейной аппроксимации и т.д.).

Графические методы свободны от погрешностей, связанных с аппроксимацией ВАХ, они позволяют учесть нелинейность ВАХ для конкретных значений параметров.

Аналитические методы позволяют получить решение в общем виде. Анализ такого решения выявляет особенности процесса при изменении всех параметров цепи.

1. Анализ переходных процессов методом

ГРАФИЧЕСКОГО ИНТЕГРИРОВАНИЯ

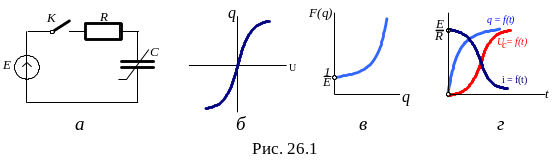
Метод применим к НЭЦ постоянного тока. Рассмотрим метод на примере анализа электрической цепи, приведенной на рис. 26.1, а. Цепь содержит последовательно соединенные источники ЭДС-Е, ключ К, линейное сопротивление R и нелинейную емкость С. Кулонвольтная характеристика емкости приведена на рис. 26.1, б.

Полагая, что в схеме нулевые начальные условия, построить графики:

Решение:

Составляем дифференциальное уравнение

Разделим переменные

(26.1)

где

. (26.2)

Для построения графика F(q) используем кулонвольтную характеристику. Задаемся произвольным значением q по характеристике q=f(U) определяем U_C и по формуле (26.2) рассчитываем F(q). Так, при q=0, U_C=0 и .

При U_C=Е . График f(q) приведен на рис. 26.1, в.

Определяем кривую q=f(t). Для этого левую часть выражения (26.1) интегрируем по t от 0 до t; а правую- по q от 0 до q. Получаем

. (26.3)

Интеграл представляет площадь, ограниченную кривой F(q), осью ординат и значением q. Значит, для определения времени t, соответствующего конкретному значению q надо подсчитать площадь, выраженную интегралом и умножить её на значение R (см. рис. 26.1, г).

С помощью кривых q=f(U) и q=f(t) строят зависимость U_C=f(t). Для этого по кулонвольтной характеристике задаваясь произвольным значением U_C находят соответствующее значение q. Далее переходят к графику q=f(t) и по заданному q находят соответствующее значение t. Качественный график зависимости U_C=f(t) приведен на рис. 26.1, г.

Зависимость i=f(t) рассчитывается по формуле

с использованием графика U_C=f(t).

2. Анализ нэц методом кусочно-линейной

АППРОКСИМАЦИИ

В основу этого метода положено применение классического метода анализа переходных процессов в ЛЭЦ на линейных участках ВАХ НЭ.

Пусть анализу подлежат цепи, приведенные на рис. 26.2, а и 26.2, в.

Цепи содержат нелинейное сопротивление, ВАХ которого приведена на рис. 26.2, б. Необходимо определить закон изменения тока в цепях.

Суть метода заключается в том, что ВАХ НС заменяется отрезками прямых. На интервале каждого отрезка применяется классический метод анализа переходных процессов. Поэтому на первом этапе ВАХ НЭ заменяем двумя отрезками прямых линий. Пусть на участке 0 < i < i₁.

а на участке i > i₁

Для анализируемых цепей справедливы уравнения:

для цепи с индуктивностью для цепи с емкостью

В цепи с индуктивностью ток после коммутации будет возрастать от 0 до максимального. Поэтому изображающая точка на ВАХ НЭ будет перемещаться сначала по первому участку 0 < i < i₁ , а затем по второму i > i₁.

Решение для первого участка цепи с индуктивностью имеет вид:

;

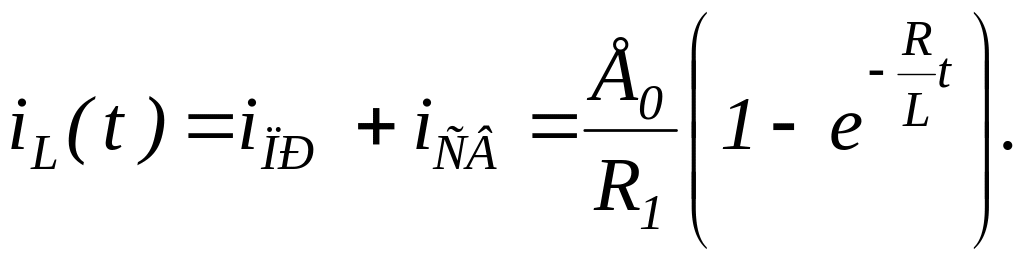
В цепи с емкостью движение изображающей точки будет противоположным, т.е. для этой цепи первым станет участок i > i₁.

; .

Постоянную интегрирования А_С находим из начального условия: при t = 0 напряжение U_C = 0. Поэтому

.

Следовательно при работе на участке i > i₁

.

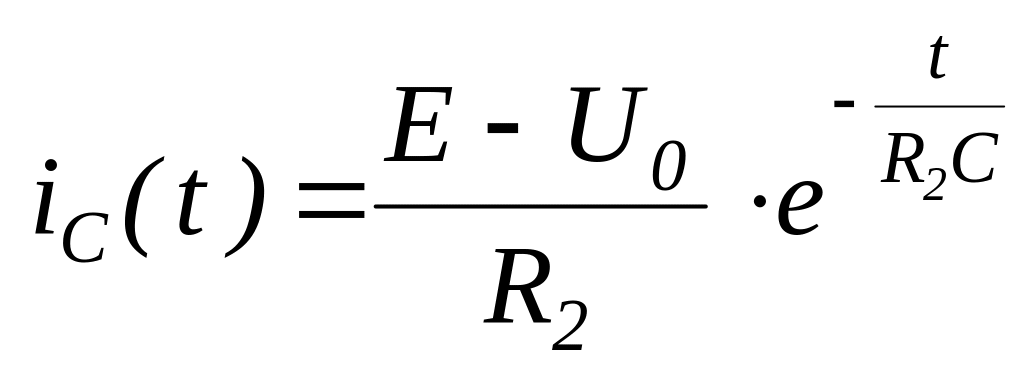Обозначим момент перехода изображающей точки от первого участка ВАХ НС ко второму t₁.

Ток через НС в этот момент равен i₁. Подставив значения t₁ и i₁ в полученные выражения и решив их относительно t₁ определим момент перехода

.

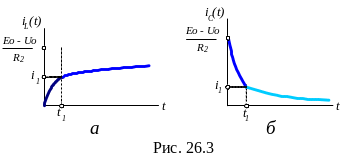
Теперь можно переходить к анализу цепей на вторых участках, но уже с ненулевыми начальными условиями. Графики зависимости приведены на рис. 26.3, а и 26.3, б соответственно.

Пример:

Для цепей, приведенных на рис. 26.2, а и 26.2, в, построить зависимость i=f(t), если,

Решение: Значение токов после коммутации

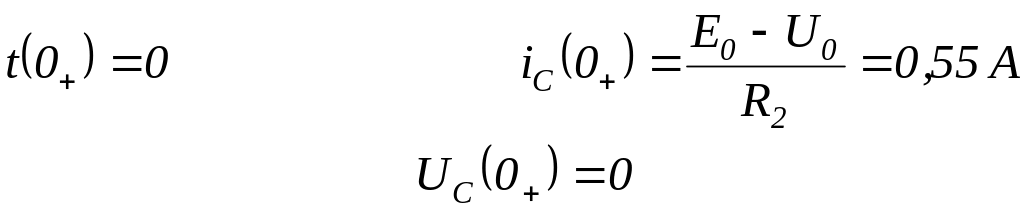
Определяем момент времени t₁, при котором токи в цепях

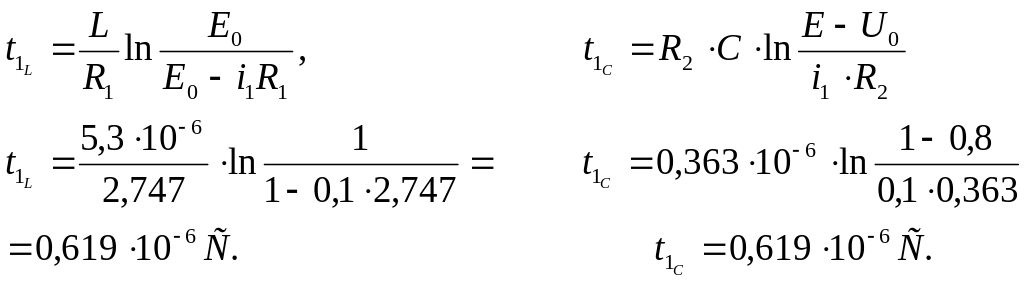
Второй участок: