Лекция 17. Анализ линейных электрических цепей при несинусоидальных воздействиях

1. Параметры несинусоидальных токов

И НАПРЯЖЕНИЙ

К основным параметрам несинусоидального тока или напряжения относятся их мгновенные, амплитудные, действующие и средние по модулю значения, а также активная и полная мощность.

Несинусоидальный ток (напряжение) можно представить суммой постоянной составляющей и гармоник. Действующее значение каждой i – ой гармоники определяется известным выражением

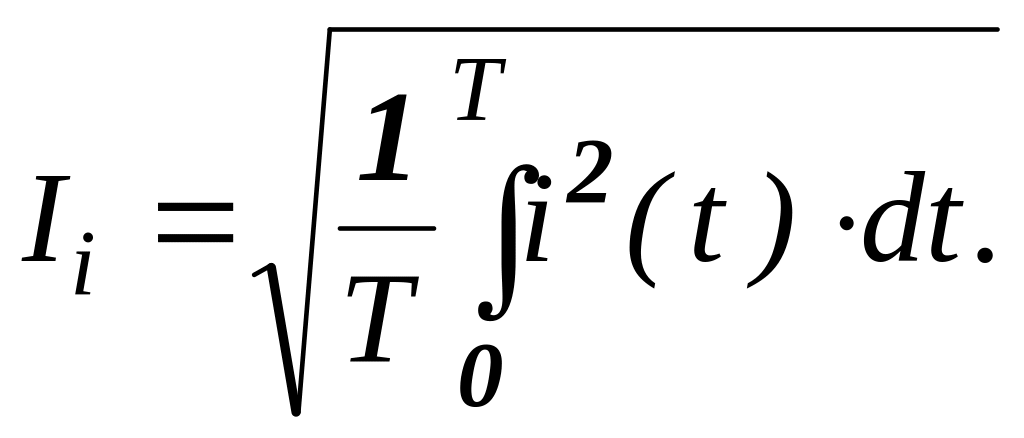
Действующее значение несинусоидального тока (напряжения) определяется геометрической суммой постоянной и действующих значений отдельных гармоник

. (17.1)

От сдвигов фаз φ_i действующее значение не зависит.

Пример. На входе двухполюсника напряжение и ток равны:

u(t) = 100 + 80·sin(ωt + 30°) + 60 sin(3ωt + 20°) + 50 sin(5ωt + 45°)B,

i(t)=33,3 + 17,87 sin(ωt - 18°) + 5,59 sin(5ωt + 120°)A/

Найти их действующие значения.

Решение.

Среднее по модулю значение несинусоидальной функции I_ср определяется выражением:

. (17.2)

Под активной мощностью Р несинусоидального тока понимают среднее значение мгновенной мощности за период первой гармоники:

Если представить напряжение и ток рядами Фурье (16.4) и проинтегрировать, то получим

Р= U₀·I₀ + U₁·I₁·cosφ₁ + U₂·I₂·cosφ₂ +…. (17.3)

Видим, что активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник.

Полная мощность S равна произведению действующего значения несинусоидального напряжения на действующее значение несинусоидального тока:

S = U·I,

где

.

Пример. Найти Р и S, если

u(t) = 25,9·sin(ωt – 11,66°) + 6·sin(3ωt + 53,83°)B;

i(t) = 3·sin(ωt – 40°) + 2,31·sin(ωt + 125°)A.

Решение.

2. Применение принципа наложения к расчету

ТОКОВ И НАПРЯЖЕНИЙ

Если на вход линейной цепи воздействуют несинусоидальные источники электрической энергии, то их токи и напряжения должны быть представлены рядом Фурье.

Согласно принципу наложения, мгновенное значение тока в любой ветви схемы равно сумме мгновенных значений токов отдельных гармоник. Аналогично, мгновенное значение напряжения на любом участке схемы равно сумме мгновенных значений напряжений отдельных гармоник на этом участке. Расчёт производят для каждой из гармоник в отдельности известными для линейных цепей методами.

Сначала рассчитывают токи и напряжения, возникающие от действия постоянной составляющей ЭДС или источника тока, затем токи и напряжения от действия первой гармоники, второй, третьей и т. д. Каждую гармонику выражают комплексным числом. Суммирование одноимённых гармоник производят путём сложения комплексных чисел или векторов на комплексной плоскости, т. е. так же как это делалось при синусоидальных воздействиях.

Пример. В левой ветви схемы рис. 17.1, а имеется источник тока i₂(t) = I_2m·cos 2ωt, во второй – источник ЭДС e(t) = E₀ + E_m·sinωt. Между индуктивностями L₃ и L₄ установлена взаимная индуктивность М.

Определить мгновенное значение тока i₃ и напряжения u_ba на зажимах L₄, если известно, что I_2m = 5А, ω = 1000 рад/сек, Е₀ = 3В, Е_m = 6В, R₁ = 3 ОМ, L₃ = 3 мГн, M = 1мГн.

Решение. Положительное направление токов в цепи показано стрелками. Для выходного контура справедливо равенство

Так как i₄ = 0, то

Чтобы использовать принцип наложения, найдём составляющие тока i₃ от каждого из источников в отдельности.

Для расчёта тока от постоянной составляющей Е₀ разомкнём ветвь с источником тока (рис. 17.1, б). Сопротивление индуктивности постоянному току равно нулю, поэтому ветвь с L₃ на рис. 17.1, б короткозамкнута. Поэтому

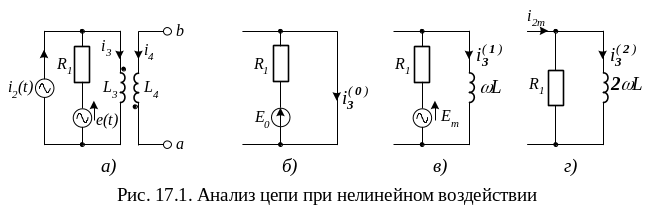
Первую гармонику тока найдём, используя схему рис. 17.1, в.

Чтобы определить вторую гармонику тока, исключим источник ЭДС и перейдём к схеме рис. 17.1, г. Согласно правилу деления токов запишем:

Мгновенное значение тока i₃ равно сумме мгновенных значений

Определяем напряжение u_ba: