3.2. Переход от изображения к функции времени.

Переход от изображения к функции времени можно проводить использованием программного продукта Mathcad, формул соответствия, приведенных в п. 1.8 или применением формулы разложения.

Применении формул соответствия между функциями оператора р и функциями времени целесообразно при наличии кратных корней в решении характеристических уравнений. Ограниченный перечень формул приводит к необходимости использования специальной литературы, что не всегда возможно.

На практике, для перехода от изображения к функции времени широко применяют формулу разложения. Рассмотрим этот путь более подробно. Изображение тока или напряжения в общем случае можно представить как отношение двух полиномов

(25.27)

Из курса математики известно, что если полином М(р) не имеет кратных корней, то правая часть (25.27) может быть представлена в виде суммы простых дробей

Оригиналом левой части полученного выражения является i(t). - производная М(р), множители у слагаемых суммы правой части - постоянные числа (не функции р), а функциями р в правой части являются только множители . Им соответствуют функции времени вида . Поэтому

(25.28)

Число слагаемых в правой части (25.28) равно числу корней уравнения М(р)= 0.

Рассмотрим несколько примеров.

Пример 4. Найти ток i₁(t) в схеме рис. 25.8 с помощью формулы разложения и сравнить с результатом решения классическим методом, если Е = 150 В, , C = 100 мкФ, u_C(0) = 50 В.

Р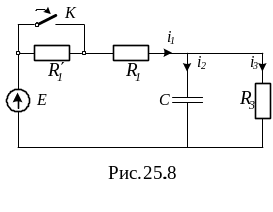 ешение. Система уравнений для изображений токов по законам Кирхгофа для схемы после коммутации (в схеме ненулевые начальные условия) имеет вид

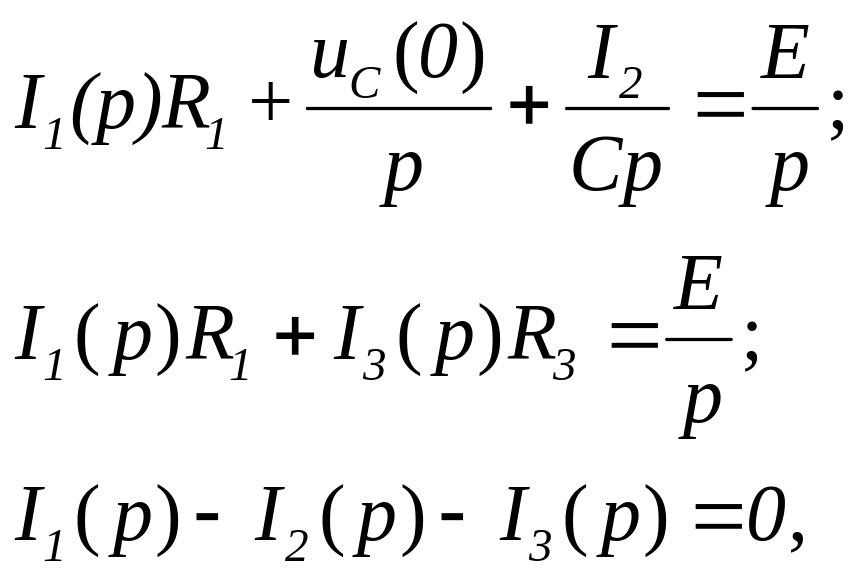
где ^_ _{внутренняя Э.Д.С., обусловленная запасом энергии в электрическом поле конденсатора к началу переходного процесса.}

_{Из системы трех уравнений найдем I1(p):}

_{Уравнение М(р) = 0 имеет корни}

_{р1 = 0 и р2 = = -400с}^-1_;

_{поэтому}

_.

_{Ток в схеме рис. 25.8 определяется выражением}

_.

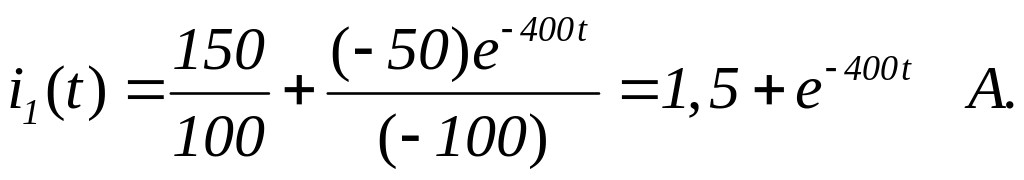_{Полученный результат совпадает} с результатом решения классическим методом.

_{Пример 5. Определить ucd(t) в схеме рис. 25.7 с помощью формулы разложения полагая R1 = R2 = 100 Ом, L1 = 1 Гн, С = 1 мкФ, а Е = 150 В.}

_{Решение.} Изображение напряжения на зажимах cd определено в примере 3 и имеет вид:

_{Находим корни полинома .}

_.

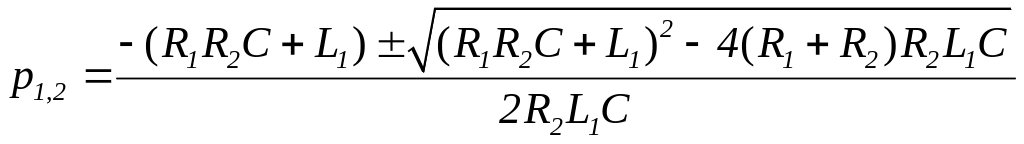_{Так как ; ,}

_то

_.

_{Следовательно р1 = -250 с}^-1_{, р2 = - 9850 с}^-1_.

_{Поэтому N(p1) = N(p2) = 1,5 10}⁴_{, производная , , ,}

_а

_.

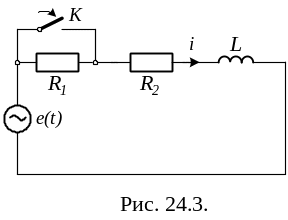
_{Пример 6. В лекции 24, стр. 99 рассмотрен пример анализа переходных процессов в схеме рис. 24.3. Проведем анализ переходных процессов в этой цепи операторным методом, применением формулы разложения и сравним трудозатраты и результаты анализа.} В схеме рис. 24.3 заданы R1 = R2 = 2 Ом; ω·L = 3 Ом; ω = 314 с^-1; Е = 127sin(ωt - 50º) В. Найти ток i(t).

Решение. Изображение синусоидальной Э.Д.С.

_{имеет вид:}

_,

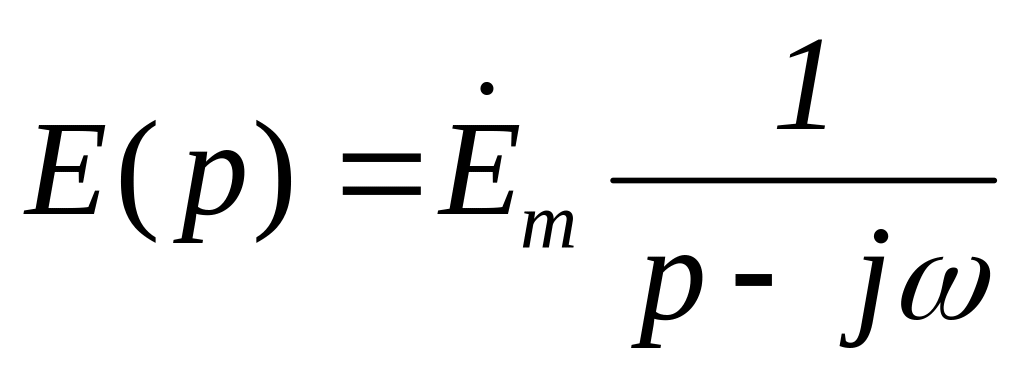_{где В.}

_{В схеме ненулевые начальные условия. Поэтому уравнение по второму закону Кирхгофа запишем в виде:}

_{. (25.29)}

_{Ток в цепи до коммутации}

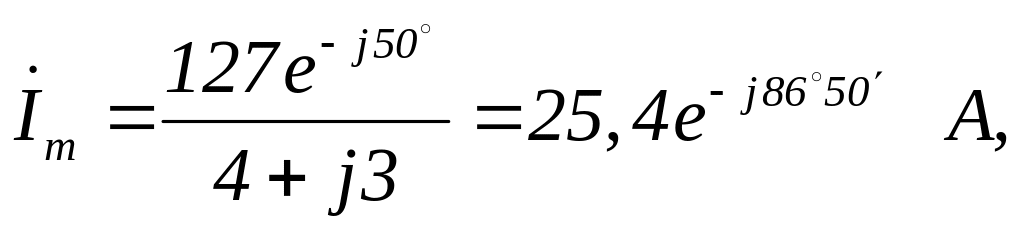
_{поэтому}

Так как действующая в схеме Э.Д.С. синусоидальна и изображение ее взято в виде 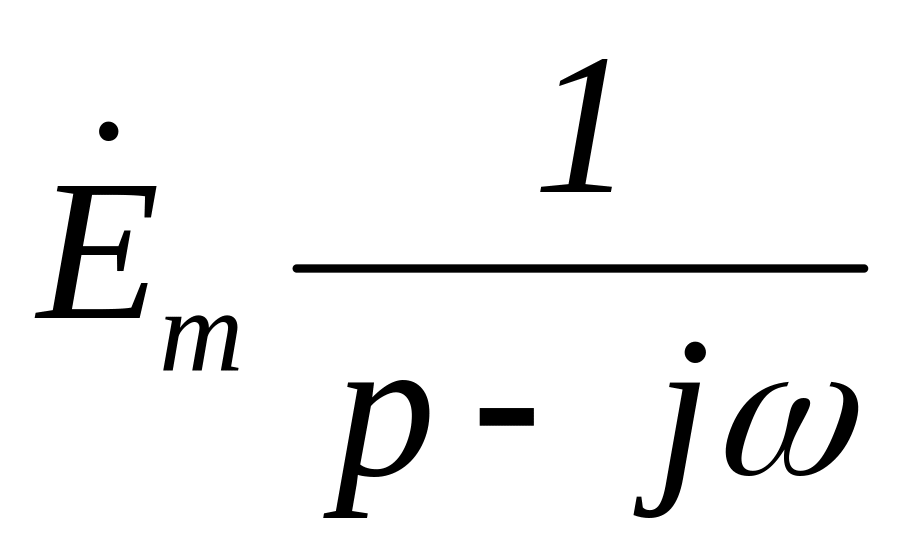, то умножим внутреннюю Э.Д.С. Li(0) на j. После преобразований из (25.29) находим I(p):

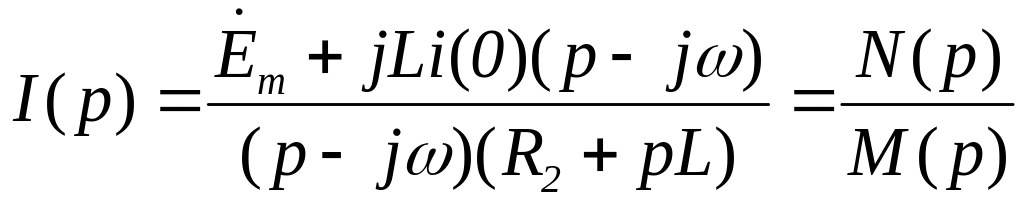
В этом выражении М(р) = 0 имеет корни:

и .

Производная от М(р)

.

Ее значения при корнях р₁ и р₂ равны:

; ;

;

.

Ток

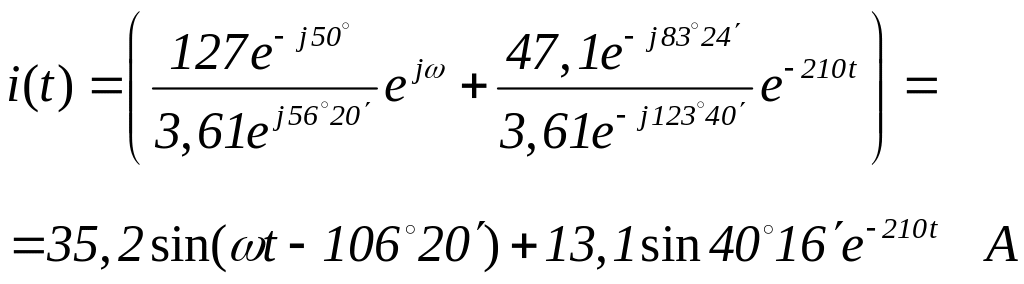
Слагаемое

.

_{Полученный результат совпадает} с результатом решения классическим методом.