2. Анализ линейных электрических цепей
ПРИМЕНЕНИЕМ КЛАССИЧЕСКОГО МЕТОДА
В этом вопросе лекции на конкретных примерах рассмотрим возможности алгоритмизации процедуры анализа переходных процессов.
2.1. Анализ переходного процесса в цепи с источником
постоянной Э.Д.С. и одним накопителем энергии
В схеме рис. 24.1
заданы
;
С = 100 мкФ; Е = 150 В.
В исходном состоянии ключ К
разомкнут, цепь находится в установившемся
режиме. При замыкании ключа в цепи
протекает переходный процесс.
Т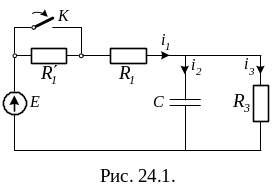
ребуется:
а) найти полные, принужденные и свободные составляющие токов и напряжения на конденсаторе, начальное значение производной от свободного напряжения на конденсаторе;
б) определить токи i1, i2, i3 и напряжение uC в функции времени.
Решение.
1. Условно положительные направления токов показаны на схеме стрелками.
2. Определяем значения токов и напряжений в схеме цепи непосредственно до коммутации и после коммутации, в установившемся режиме.
До коммутации цепь находится в установившемся режиме. В этом режиме в цепи протекают принужденные токи, а на ее участках действуют принужденные напряжения.
Постоянный ток через конденсатор не протекает, т. е.
i2пр(0-) = 0,
Токи первой и третьей ветвей равны
Принужденное напряжение на конденсаторе до коммутации равно падению напряжения на сопротивлении R3:
После коммутации цепь также переходит в установившийся режим. При этом:
i2пр(0+)
= 0,
Для определения полных токов и напряжений цепи применяем второй закон Кирхгофа. Составим уравнение для контура, образованного первой и второй ветвями при t = 0+:
i1(0+)·R1 + uC(0+) = E.
По второму закону коммутации uC(0+) = uCпр(0-) = 50 В. Поэтому полный ток первой ветви, непосредственно после коммутации, определим отношением:
Из уравнения uC(0+) = i3(0+)·R3 следует, что полный ток третьей ветви определится отношением:
Полный ток второй ветви определим на основании первого закона Кирхгофа:
Свободные составляющие найдем как разности между полными и принужденными величинами:
Чтобы определить
начальное значение производной от
свободного напряжения на конденсаторе
воспользуемся известным выражением
.
Тогда
Требования пункта а задания и пункта 2 алгоритма анализа выполнены.
3. Характеристическое уравнение для послекоммутационной схемы имеет вид
рR1R3C + R1 + R3 = 0.
Уравнение первой степени, его корень
4. Определяем выражения для искомых токов и напряжения в функции времени.
С учетом (24.1) свободные токи и напряжение uC имеют вид:
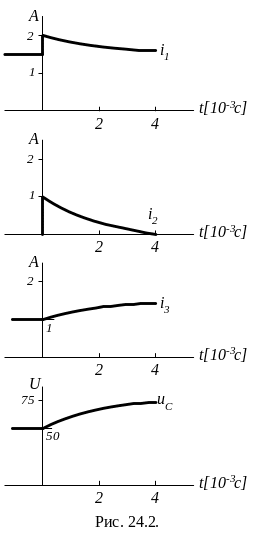
Выражения для полных токов и напряжения на емкости:
,
Графики искомых токов и напряжения приведены на рис. 24.2.
2.2. Анализ переходного процесса в цепи с источником
синусоидальной Э.Д.С. и одним накопителем энергии
В схеме рис. 24.3 заданы R1 = R2 = 2 Ом; ω·L = 3 Ом; ω = 314 с-1; Е = 127sin(ωt - 50º) В.
В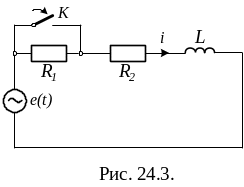
исходном состоянии ключ К
разомкнут, цепь находится в установившемся
режиме. При замыкании ключа в цепи
протекает переходный процесс.
Требуется:
а) найти iсв(0+);
б) определить закон изменения тока в цепи после коммутации.
Решение.
1. Условно положительное направление тока показано на схеме стрелкой.
2. Определяем значения токов и напряжений в схеме цепи непосредственно до коммутации и после коммутации, в установившемся режиме.
До коммутации цепь находится в установившемся режиме. В этом режиме в цепи протекают принужденные токи, а на ее участках действуют принужденные напряжения.
Комплексная амплитуда тока цепи определяется отношением:
Мгновенное значение тока до коммутации
(24.13)
В момент непосредственно до коммутации (при ωt = 0)
Определяем комплексную амплитуду принужденного тока после коммутации
Мгновенное значение принужденного тока после коммутации
(24.14)
В момент непосредственно после коммутации (при ωt = 0)
По первому закону коммутации в ветви с индуктивностью ток в момент коммутации сохраняет значение, которое он имел до коммутации, а после коммутации плавно изменяется от этого значения:
Но
Следовательно
3. Характеристическое уравнение для схемы после коммутации имеет вид рL + R2 = 0. Это уравнение первой степени, его корень
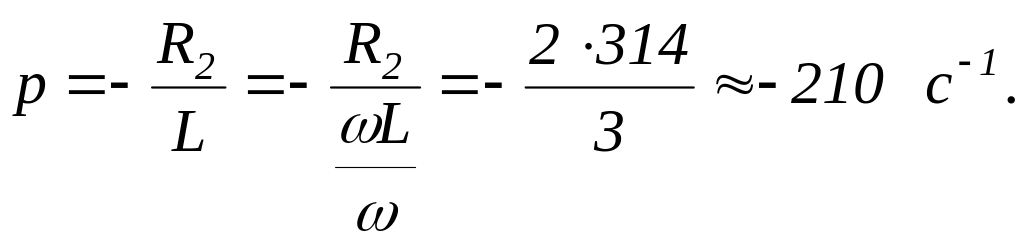
4. Определяем выражения для искомых токов в функции времени.
С учетом (24.1) свободный ток цепи равен
График этого тока представлен кривой 1 на рис 24.4.
П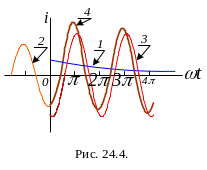
ринужденный
ток цепи до коммутации определяется
выражением (24.13), а его график представлен
кривой 2
на рис. 24.4.
Принужденный ток после коммутации определяется выражением (24.14), а его график представлен кривой 3 на рис. 24.4.
Полный ток цепи
График этого тока представлен кривой 4 на рис.24.4 (ординаты кривой 4 при ωt > 0 равны сумме ординат кривых 1 и 3).