2. Анализ переходных процессов в неразветвленных
ЦЕПЯХ
Выражения (22.1) и (22.2) называют линейными дифференциальными уравнениями. Решение таких уравнений позволяет определить значение тока через индуктивность или напряжения на емкости как функцию времени. В настоящее время разработано несколько методов решения линейных дифференциальных уравнений: классический, операторный и метод с использованием интеграла Дюамеля.
Приемы расчета переходных процессов в простейших неразветвленных электрических цепях, рассматриваемые в данном вопросе лекции следует рассматривать как введение к классическому методу анализа переходных процессов.
2.1. Заряд и разряд ёмкости через резистор
П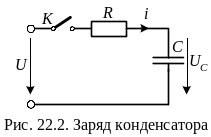
усть
задана цепь, приведенная на рис. 22.2.Для
такой цепи справедливо равенство
(22.3)
Полученное выражение представляет собой линейное дифференциальное уравнение. Интеграл от такого уравнения представляет сумму частного решения неоднородного уравнения и общего решения однородного уравнения. Токи и напряжения, полученные в результате частного решения, называют установившимися или принуждёнными iу, uу, iпр, uпр.
Однородное уравнение получаем при равенстве нулю правой части (22.3). Токи и напряжения, полученные в результате общего решения, определяются лишь параметрами элементов цепи и называются свободными iсв, uсв.
Сумма установившихся и свободных токов и напряжений определяют переходные токи и напряжения:
uпер = uу +uсв.
Частное решение находят для установившегося режима, когда переходный процесс закончен. Для рассматриваемой цепи при t→∞
uсу = U.
Выражение для свободного напряжения uсв определяется решением однородного дифференциального уравнения
Преобразуем его к виду:
Решением этого
уравнения является функция
.
Здесь А –
постоянный коэффициент, р – корень
характеристического уравнения
.
Нетрудно видеть,
что корень этого уравнения
.
Таким образом
.
Видим, что свободная составляющая напряжения на емкости в момент коммутации скачком принимает значение А. Величину τ = RC называют постоянной времени. Она имеет размерность времени и характеризует длительность переходного процесса, т. е. время, в течение которого uСсв уменьшается в е раз по сравнению с начальным значением uСсв (0) = А.
С учётом полученных выражений можем записать
.
Для определения А воспользуемся вторым законом коммутации. В момент , предшествующий коммутации, конденсатор С был разряжен. Следовательно, и в первый момент после коммутации напряжение на емкости останется без изменения. Значит, можем записать
UC(0+) = U + A = 0
и
А = -U.
Теперь очевидно, что
.
Ток в цепи во время переходного процесса
,
т. е., ток в цепи с
емкостью изменяется скачком до значения
.
Графики напряжения и тока анализируемой цепи приведены на рис. 22.3.
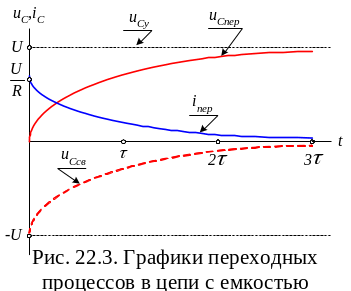
Переходный ток цепи с ёмкостью может изменяться скачком. Если активное сопротивление цепи мало, то ток в момент включения источника напряжения может быть значительно больше номинального значения.
При разряде
конденсатора
ёмкостью С,
заряженного
до напряжения U0,
на резистор
R
необходимо учитывать, что и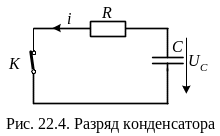
сточник
в цепи отсутствует и
.
Напряжение
.
Ток при разряде конденсатора не совпадает
по направлению с напряжением uС,
поэтому
Согласно второму закону Кирхгофа
uСсв - R·i = 0.
или
.
Это однородное дифференциальное уравнение. Его решение имеет вид
.
В момент t = 0 uСсв = U0, поэтому А = U0. Следовательно
.
Переходной ток определяется выражением
.
Длительность переходного процесса при разряде, так же как и при заряде ёмкости, определяется постоянной времени τ.