3. Феррорезонансный стабилизатор напряжения

Для стабилизации напряжения переменного тока широко применяют различные феррорезонансные схемы. Одна из них представлена на рис.20.5, а. Схема содержит параллельный феррорезонансный контур и последовательно с ним включенную линейную индуктивность L.

На рис. 20.5, б приведены: ВАХ нелинейной индуктивности 1, ВАХ емкости 2, ВАХ параллельного феррорезонансного контура 3, ВАХ линейной индуктивности 4. Результирующая ВАХ всей схемы – кривая 5. Ее ординаты равны алгебраической сумме ординат кривой 3 и прямой 4.

Принцип стабилизации напряжения заключается в том, что выходное напряжение U_вых снимается с такого элемента цепи, на котором оно по величине остается постоянным или изменяется незначительно, при изменении входного напряжения U_вх. В рассматриваемом примере выходное напряжение снимается с нелинейной индуктивности, а его изменение определяется участком а-б кривой 5. Очевидно, что изменение U_вых остается существенным.

Для улучшения качества стабилизации в схему включается дополнительная линейная индуктивность с числом витков (на схеме показана пунктиром). Теперь напряжение на выходе стабилизатора равно напряжению на зажимах а-б минус Э.Д.С., наводимая на обмотке . Последняя линейно зависит от тока I (прямая 6 рис. 20.5, б). Напряжение на выходе стабилизатора изобразится кривой 7. Ординаты кривой определяются разностью соответствующих ординат кривой 5 и прямой 6.

Зависимость напряжения на выходе стабилизатора U_вых от напряжения на входе U_вх при холостом ходе приведена на рис. 20.5, в. Для построения характеристики необходимо задавать току произвольные значения и для каждого из них по кривым 7 и 5 находить соответствующие величины U_вых и U_вх.

Стабилизация имеет место только при U_вх > U₁. Поэтому в область значений U_вх < U₁ график рис. 20.5, в не продолжен.

Лекция 21. Трансформатор. Основные соотношения.

Принцип работы трансформатора с ферромагнитным сердечником рассмотрен в лекции 7. Определены результирующий магнитный поток

(21.1)

и коэффициент трансформации

.

Однако вопросам учета потерь на активных сопротивлениях обмоток, потерь, возникающих в результате потоков рассеяния реальных устройств, учету нелинейности цепи не было уделено внимание. Кроме того, не оценены основные параметры трансформатора, не рассмотрены режимы его работы.

1. Основные параметры трансформатора

Помимо основного магнитного потока Ф (по 21.1) в реальном трансформаторе существуют потоки рассеяния первичной и вторичной обмоток. Для количественной оценки потоков и вводят понятие эквивалентной индуктивности рассеяния так, что

; .

Кроме того, обмотки реального трансформатора обладают активными

сопротивлениями R₁ и R₂. Чтобы учесть перечисленные величины при анализе работы трансформатора, переходят к его схеме замещения (рис. 21.1).

.

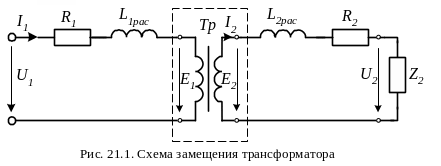
Часть схемы, выделенная на рис. 21.1 пунктиром, не имеет активных сопротивлений и потоков рассеяния, а поэтому называется идеализированным трансформатором. К нему применимы все соотношения, полученные в лекции 7. Однако для получения простых и наглядных соотношений параметров трансформатора необходимо преодолеть еще одну трудность.

Дело в том, что трансформатор в расчетном эквиваленте представляет со­бой нелинейную цепь. Значит, к его анализу необходимо применять теорию не­линейной алгебры. Чтобы уйти от этого, гистерезисную зависимость В = f(H) заменяют эквивалентным эллипсом (рис. 21.2), построенным так, что его пло­щадь не менее чем на 95% перекрывает площадь петли гистерезиса. Если те­перь зависимости B = f(H), ; выражать через параметры эллипса, то возникающие за счет отклонения от петли гистерезиса погрешно­сти оказываются пренебрежимо малыми для практических целей.

Г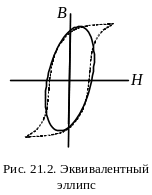 лавное в том, что переход к параметрам эквивалентного эллипса позволяет получить простые линейные выражения в представлении величин В(t) и Н(t) с помощью тригонометрических функций:

, (21.2)

, (21.3)

где - сдвиг фазы между Н(t) и В(t).

От выражений (21.2) и (21.3) легко перейти к показательной комплексной форме представления. Тогда

; , (21.4)

Учитывая соотношения (5.10), (18.1) и (21.4), связь между напряжением и магнитной индукцией представим в виде:

,

а связь между током и напряженностью магнитного поля выражением:

. (21.5)

Теперь можно перейти к оценке основных параметров трансформатора. Учитывая (5.10), (18.1) и (21.4), определяем напряжение на первичной и вторичной обмотках трансформатора:

, (21.6)

. (21.7)

Эти напряжения полностью уравновешиваются Э.Д.С. первичной и вторичной обмоток:

, (21.8)

. (21.9)

Отношение (21.6) к (21.7):

(21.10)

называется коэффициентом трансформации.

Подставим в выражение для значение Ф из (21.1):

. (21.11)

Если разомкнуть цепь вторичной обмотки, то ее ток I₂ станет равным

нулю. При этом в цепи первичной обмотки будет протекать ток холостого хода, т.е. I₁ = I_1x , а выражение (21.11) примет вид:

. (21.12)

Но - это напряжение источника. Оно не зависит от режима работы трансформатора. Значит, левые части равенств (21.11) и (21.12) равны.

Отсюда следует, что равны и правые части. Приравнивая их, определим ток

холостого хода трансформатора.

. (21.13)

Последнее выражение показывает, что ток холостого хода равен разности токов первичной и вторичной обмоток, причем ток вторичной обмотки пересчитан к виткам первичной обмотки. Ток холостого хода мал и у мощных трансформаторов составляет единицы процентов от номинального значения.

Произведение

называют приведенным током вторичной обмотки. Для оценки качества трансформатора кроме пользуются приведенным сопротивлением нагрузки и приведенным напряжением вторичной обмотки . Определим их значения. Для этого выразим магнитный поток Ф из (21.7)

. (21.14)

Подставим (21.14) в (21.6):

.

Помножим и разделим последнее выражение на коэффициент Перегруппировав множители, получим:

. (21.15)

В выражении (21.15) - приведенный ток, а - приведенное, т.е. пересчитанное к виткам первичной обмотки, сопротивление нагрузки. Произведение

(21.16)

называется приведенным напряжением вторичной обмотки. Очевидно, что

. (21.17)

С учетом введенных понятий выражение (21.13) для тока холостого хода принимает вид:

. (21.18)

В выражении (21.12) множитель

определяет индуктивность первичной обмотки. Поэтому можно записать:

,

что полностью соответствует закону Ома для цепи с индуктивностью.

Для завершения анализа принципа работы построим векторную диаграмму идеализированного трансформатора (рис.21.3). На диаграмме в качестве исходного принимаем вектор магнитного потока . Векторы Э.Д.С. отстают от вектора на 90⁰. Это очевидно из (21.8) и (21.9) по наличию множителя (-j). Векторы и равны по величине векторам и соответственно, но противоположны им по направлению.

Вектор тока холостого хода опережает вектор на угол . Это

хорошо видно из (21.5), т.к.

.

Вектор тока вторичной обмотки трансформатора сдвинут относительно вектора на угол ₂, что определяется характером нагрузки

.

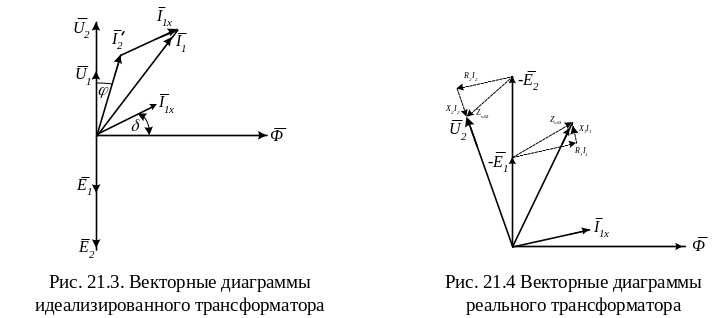
Значение вектора легко найти по (21.18)

,

что и выполнено на диаграмме.

Для перехода к реальному трансформатору обратимся к рис. 21.1. Схема рис. 21.1 содержит два электрически не связанных замкнутых контура – цепь первичной и цепь вторичной обмоток. Для каждой из них справедлив второй закон Кирхгофа. Поэтому для цепи первичной обмотки трансформатора справедливо равенство

. (21.19)

Равенство (21.19) показывает, что напряжение источника уравновешивается падением напряжения на комплексном сопротивлении первичной обмотки и наводящейся в ней ЭДС самоиндукции . Эпюры напряжений, соответствующие (21.19), приведены на рис. 21.4.

Для цепи вторичной обмотки трансформатора можно записать равенство

. (21.20)

Эпюры напряжения, соответствующие (21.20), приведены на рис. 21.4.