161

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Инженерно технический институт

Кафедра электропривода и электротехники

Теоретические основы электротехники

Часть II.

Для студентов специальностей

220201, 220301 ЧГУ.

ЧЕРЕПОВЕЦ

2009

Нохрин А. Н.

Теоретические основы электротехники. Курс лекций. Часть II. Череповец, 2009.

Курс лекций «Теоретические основы электротехники» часть II соответствует утвержденным учебным планам по специальности 140604 – “Электропривод и автоматика промышленных установок и технологических комплексов”.

Курс рассчитан на 38 часов лекций. В нем представлено 14 лекций по пяти темам. Достаточно подробно рассмотрены воздействия несинусоидальных токов и напряжений на ЛЭЦ, НЭЦ переменного тока, переходные процессы в линейных и нелинейных электрических цепях, параметры и режимы работы линий с распределенными параметрами и электрические фильтры.

Лекции рассмотрены и одобрены на заседании кафедры ЭП и ЭТ, протокол № 4 от 24.12.09, одобрены редакционной комиссией ИТИ, протокол № 4 от 10.02.10.

Рецензенты: А. М. Водовозов – к. т. н., доцент, зав. кафедрой управляющих

вычислительных систем ВГТУ;

В, А. Шабалов – к. т. н., профессор кафедры ВТ и СУ ИЭИ ЧГУ.

Тема VI

Несинусоидальные токи и напряжения

В линейных электрических цепях

Лекция 16. Представление несинусоидальных токов и напряжений

1. Определение периодических несинусоидальных

ТОКОВ И НАПРЯЖЕНИЙ

Периодические токи и напряжения, изменяющиеся во времени по закону отличному от гармонического, называются несинусоидальными. Несинусоидальные токи и напряжения возникают в электрической цепи при следующих условиях:

– когда источник ЭДС или тока даёт несинусоидальные колебания, а все элементы цепи линейны;

– если источник ЭДС или тока даёт синусоидальные колебания, но один или несколько элементов цепи нелинейны;

– когда источник ЭДС или тока даёт несинусоидальные колебания, а в составе цепи один или несколько элементов цепи нелинейны;

– если источник ЭДС или тока даёт синусоидальные колебания, все элементы цепи линейны, но один или несколько элементов изменяются во времени.

В лекции рассматриваются способы представления несинусоидальных сигналов, особенности работы и анализа линейных электрических цепей при воздействии таких сигналов.

2. Представление периодических несинусоидальных

ТОКОВ И НАПРЯЖЕНИЙ РЯДОМ ФУРЬЕ

Из курса математики известно, что любую периодическую функцию u(t) c периодом T, удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье. В электротехнике все практически используемые функции удовлетворяют условиям Дирихле, поэтому производить проверку не требуется.

Обозначим основную частоту

ω₀ =

Таким образом, период функции по переменной (ωt) равен 2π, а во времени период той же функции равен Т.

Представление функции рядом Фурье имеет вид:

(16.1)

где U₀ – постоянная составляющая, а_i, b_i – амплитудные значения синусных и косинусных гармоник соответственно.

Постоянная составляющая U₀ и амплитуды гармоник определяются выражениями:

(16.2)

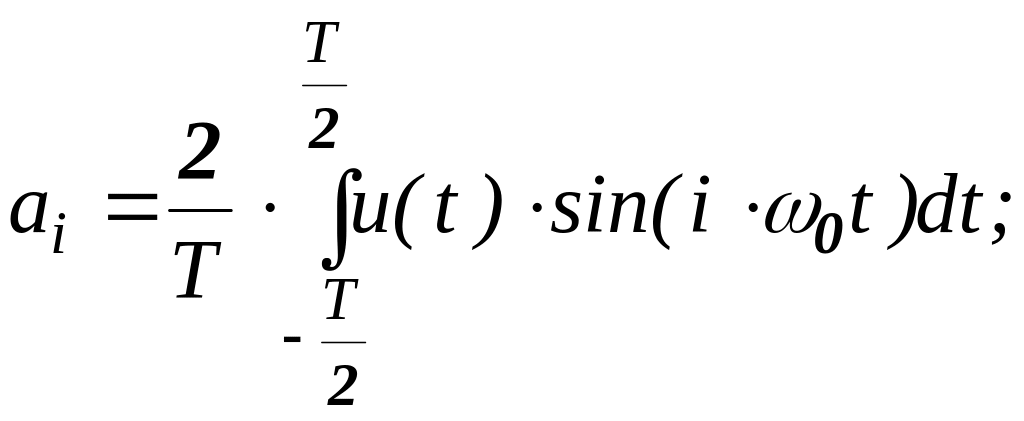(16.3, а)

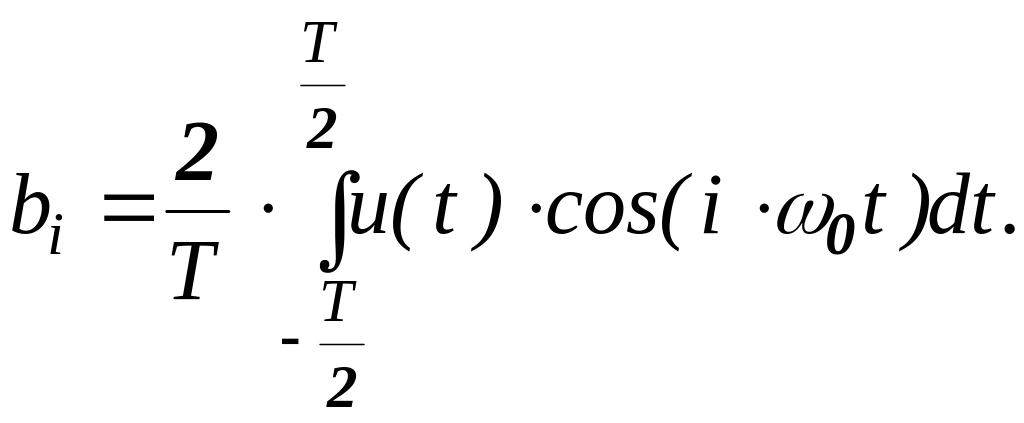(16.3, б)

Так как

где

, а ,

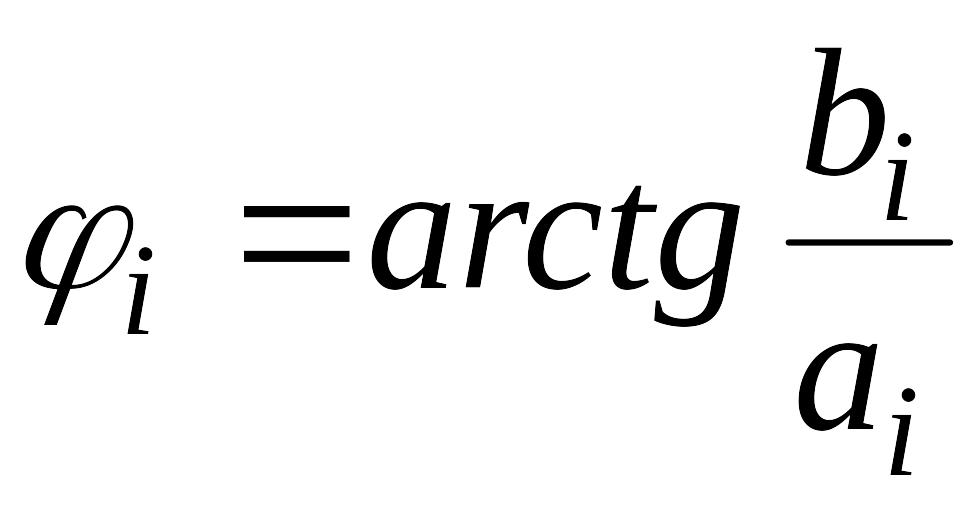то ряд Фурье можно записать в другой форме:

(16.4)

где U_i – амплитуда i – й гармоники ряда Фурье.

Гармоники, для которых i – нечётное число, называют нечётными, для которых i – чётное число, называют чётными.

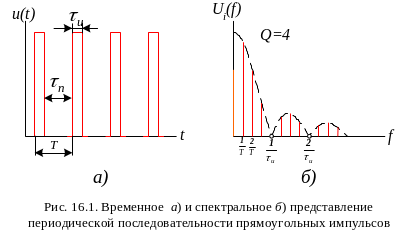
Представление сигналов в зависимости от времени позволяет наблюдать их в плоскости амплитуда – время. Представление сигналов рядом Фурье позволяет наблюдать их в плоскости амплитуда – частота. Так, временное представление периодической последовательности прямоугольных импульсов (рис. 16.1, а) имеет вид

, (16.5)

где U_i – амплитуда i – го импульса, – фронт, – срез, а τ_i – длительность i – го импульса. Этот же сигнал можно представить рядом (16.4), т. е. наблюдать его спектр (рис. 16.1, б).

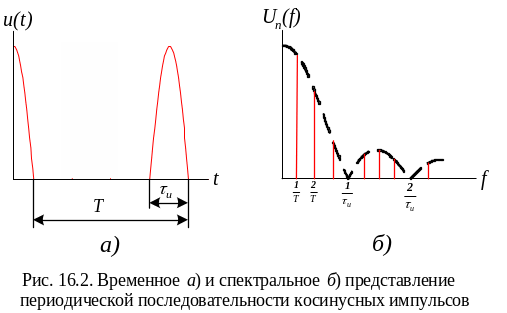
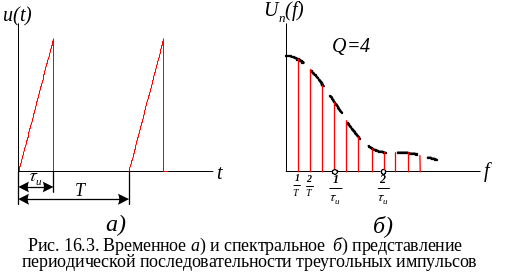
Для примера и взаимного сравнения на рис. 16.2 и рис. 16.3 приведены спектры периодической последовательности косинусных и треугольных импульсов.

Совокупность в (16.4) модулей U_i образуют амплитудно-частотный спектр периодической функции u(t), а совокупность фаз φ_i – фазо-частотный. Амплитудный спектр периодических функций является дискретным или линейчатым. В нём отдельные спектральные составляющие следуют с частотным интервалом .

Определим комплексную форму ряда Фурье. Для этого учтём, что

Следовательно,

. (16.6)

Подставив (16.6) в (16.4) получим

. (16.7)

Обозначим

Тогда ряд (16.7) можно записать в виде

(16.8)

Формула (16.8) представляет собой ряд Фурье в комплексной форме. В ней индекс i может принимать все целые числовые значения от - ∞ до + ∞, но не может равняться нулю, так как постоянная составляющая ряда выделена в виде отдельного слагаемого.

Модуль комплексной амплитуды спектральной составляющей можно переписать в алгебраической форме:

(16.9)

Но а_i и b_i определяются выражениями (16.3). Применяя их к выражению (16.9) получим

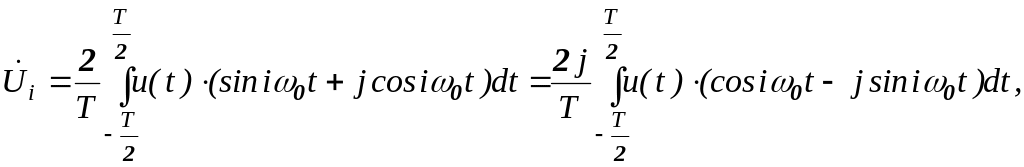
или

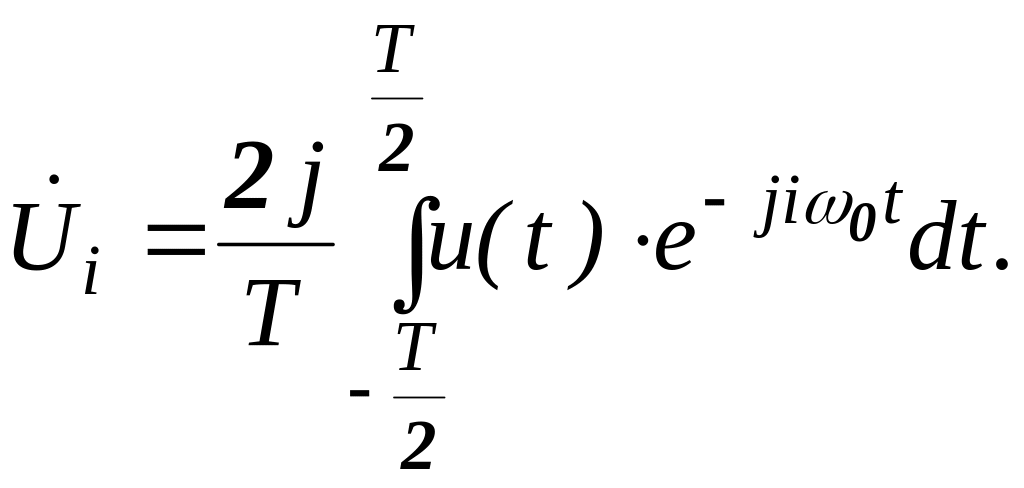(16.10)

Подставляя правую часть формулы (16.10) в формулу (16.8) будем иметь

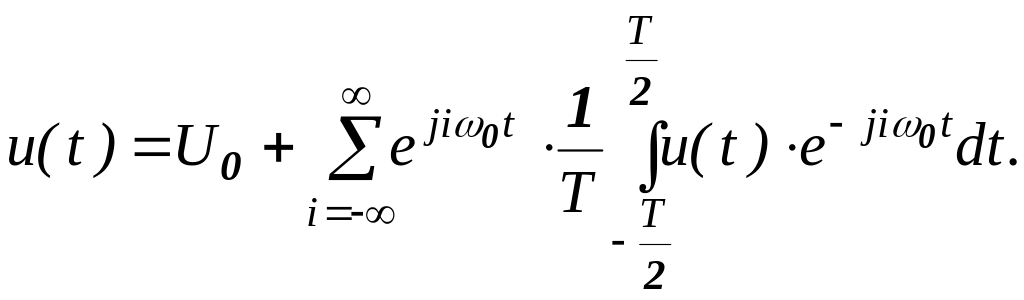(16.11)