Приложение. Как переносить данные в Ехсеl и отображать графики зависимостей
Пусть Вам необходимо отобразить в виде графика данные, которые находятся в файле. Вначале Вам необходимо скопировать эти данные в буфер обмена, используя, к примеру, Far. Для этого выберите режим редактирования файла, нажав клавишу F4 на имени файла, выделите необходимые Вам данные клавишами управления курсором (с прижатой Shift), нажатием Ctrl+Ins скопируйте помеченный блок в буфер обмена. Далее определите, какой вид у этих данных:
одна строка произвольной длины
один столбец произвольной длины
два столбца произвольной длины, первый из которых содержит независимую переменную, а второй – зависимую.
две строки произвольной длины, первая из которых содержит независимую переменную, а вторая – зависимую.
две строки длины до 64 чисел каждая, первая из которых содержит независимую переменную, а вторая – зависимую.
Случаи большего числа строк (столбцов) сводятся к этим пяти.
Запустите редактор Word и комбинацией Shift+Ins вставьте содержимое буфера обмена. Произведите замену точек на запятые: нажатием Ctrl+H вызовите диалоговое окно Найти и заменить, в поле Найти ввести точку, в поле Заменить на – запятую и нажать на клавишу Заменить все.
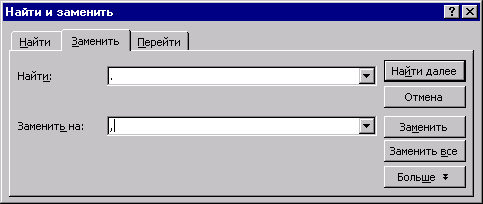
Рассмотрим возможные случаи:
Этот случай сводится ко второму заменой пробелов на символы абзаца:
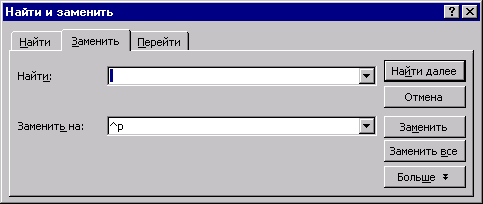
3, 5. Комбинацией Ctrl+А выделите весь текст в окне. Затем в пункте меню Таблица выберите пункт Преобразовать в таблицу.
В появившемся диалоговом окне в качестве символа разделителя введите пробел (поле другой) и нажмите на клавишу ОК.
4. А не транспонировать ли Вам данные перед выводом в файл? Сводится к случаю 3.
Следующий этап – выделение всего содержимого окна (Ctrl+А) и копирование выделенного фрагмента в буфер обмена (Ctrl+Ins), затем – запуск табличного процессора Excel и вставка содержимого буфера обмена нажатием Shift+Ins. Не снимая пометки, выберите пункт меню Вставка, а в нём – подпункт Диаграмма:
1, 2. В списке Тип выберите пункт График, а в разделе Вид – первый из предложенных видов графиков и нажмите на кнопку Готово.
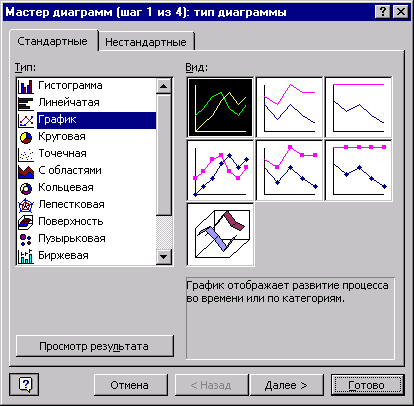
3, 4, 5. В списке Тип выберите пункт Точечная, а в разделе Вид – третий из предлагаемых видов графиков и нажмите на кнопку Готово.
Литература
Алгоритмы и программы восстановления зависимостей. – М.: Наука, 1984.
Анго А. Математика для электро- и радиоинженеров. – М.: Наука, 1964.
Бабак В.П., Хандецький В.С., Шрюфер Е. Обробка сигналів. – К.: Либідь, 1996.
Боглаев Ю.П. Вычислительная математика и программирование: Учебное пособие для студентов втузов. – М.: Высшая школа, 1990.
Вайнер Р., Пинсон Л. С++ изнутри. – Киев: ДиаСофт, 1993.
Вентцель Д.А., Вентцель Е.С. Элементы теории приближенных вычислений. – М.: Издательство ВВИА им. Н.Е. Жуковского, 1949.
Вентцель Е.С. Исследование операций. – М.: Радио и связь, 1970.
Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969.
Гавурин М.К. Лекции по методам вычислений. – М.: Наука, 1971.
Гантмахер Ф.Р. Теория матриц. – М.: Государственное издательство технико-теоретической литературы, 1953.
Гринчишин Я.Т., Ефимов В.И., Ломакович А.Н. Алгоритмы и программы на Бейсике. – М.: Просвещение, 1988.
Гринчишин Я.Т. TURBO PASCAL: Чисельні методи в фізиці та математиці: Навч. посібник – Тернопіль, 1994.
Гулд Х., Тобочник Я. Компьютерное моделирование в физике: В 2-х частях. Часть 2: Пер. с англ. – М.: Мир, 1990.
Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. – М.: Наука, 1970.
Дамбраускас А.П. Симплексный поиск. – М.: Энергия, 1979.
Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Физматгиз, 1963.
Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. – М.: Наука, 1967.
Джордж А., Лю Дж. Численное решение больших разряжённых систем уравнений. – М.: Мир, 1984.
Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. – М.: Наука, 1987.
Иванов В. В. Методы вычислений на ЭВМ: Справочное пособие. – К.: Наукова думка, 1986.
Кантор И.Л., Солодовников А.С. Гиперкомплексные числа. – М. Наука, 1973.
Лукас П. С++ под рукой. – Киев: ДиаСофт, 1993.
Лукомский Я.И. Теория корреляции и её применение к анализу производства. – М.: Госстатиздат ЦСУ СССР, 1961.
Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир, 1977.
Маликов В.Т., Кветный Р.Н. Вычислительные методы и применение ЭВМ: Учебное пособие. – К.: Выща школа, 1989.
Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. – Томск: Раско, 1991.
Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. – М.: Наука, 1986.
Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике. – М.: Высшая школа, 1983.
Полищук А.П. Персональный компьютер и его программирование (С, С++, Паскаль). Учебно-справочное пособие. – Кривой Рог: КГПИ, 1997.
Попов В.С., Мансуров Н.Н., Николаев С.А. Электротехника. – М.: Издательство Министерства коммунального хозяйства РСФСР, 1958.
Смирнов В.И. Курс высшей математики. Т. 1-5. – М.: Наука, 1974.
Статистическая обработка результатов экспериментов на микро-ЭВМ и программируемых калькуляторах. – Л.: Энергоатомиздат, 1991.
Страуструп Б. Язык программирования С++: В 2-х частях. – К.: Диасофт, 1993.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. Учебное пособие для вузов. – М.: Наука, 1986.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.-Л.: Государственное издательство технико-теоретической литературы, 1951.
Уилкинсон Дж., Райнш К. Справочник алгоритмов на языке Алгол. Линейная алебра. – М.: Машиностроение, 1976.
Уткіна С.В., Наришкіна Л.С. Алгебра і числові системи: Навч. посібник. – К.: Вища школа, 1995.
Фаддеева В.Н. Вычислительные методы линейной алгебры. – М.: Гостехиздат, 1950.
Фейсон Т. Объектно-ориентированное программирование на Borland C++ 4.5. – Киев: Диалектика, 1996.
Форсайт Д., Малькольм М., Моллер К. Машинные методы математических вычислений. – М.: Мир, 1980.
Форсайт Д., Моллер К. Численное решение систем линейных алгебраических уравнений. – М.: Мир, 1968.
Хемминг Р.В. Численные методы. – М.: Наука, 1968.
Шуп Т.Е. Прикладные численные методы в физике и технике. – М.: Высшая школа, 1990.
Шуп Т.Е. Решение инженерных задач на ЭВМ. Практическое руководство. – М.: Мир, 1982.
Учебное пособие
Александр Павлович Полищук
Сергей Алексеевич Семериков
Методы вычислений в классах языка С++
Подп. к печати 28.12.98 Бумага офсетная №1 Усл. кр.-от. 18,38 Тираж 500 |
Формат 80х84 1/16. Усл. печ. л. 18,38 Уч.-изд. л. 22,29 Зак. №12-2483 |
КГПИ, 324086, Кривой Рог-86, пр. Гагарина, 54
Криворожская городская типография