Глава IX

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ТЕЛ ПРОЕЦИРУЮЩИМИ ПЛОСКОСТЯМИ.

ПОСТРОЕНИЕ ОРТОГОНАЛЬНЫХ

ПРОЕКЦИЙ, ЛИНИЙ СРЕЗА, АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ И РАЗВЕРТОК ПОВЕРХНОСТЕЙ УСЕЧЕННЫХ ГЕОМЕТРИЧЕСКИХ ТЕЛ

Многие детали, применяемые в технике, имеют различные срезы, выполненные, напри­мер, фрезерованием, строганием, обрезкой и т. п. Выработка умения строить срезы в ортогональных проекциях, в аксонометрии и на развертках является одной из важных за­дач обучения черчению. Так как форма любой детали представляет собой совокупность геометрических тел, вопросы построения сре­зов рассматривают сначала на геометриче­ских телах.

При построений геометрических тел со срезами условимся, что отсеченная плоско­стью часть геометрического тела, отбрасы­вается, а оставшуюся усеченную часть гео­метрического тела ограничивает фигура сре­за (срез).

§ 31. Пересечение многогранников проецирующей плоскостью

Если многогранник рассечь плоскостью, то линия пересечения поверхности многогранника с плоскостью будет замкнутой плоской лома­ной линией, т. е. многоугольником. Каждая вер­шина этого многоугольника есть точка, в кото­рой плоскость пересекла его ребро. Каждая сторона многоугольника есть отрезок прямой линии, по которой плоскость пересекла грань многогранника. Значит для того, чтобы по­строить линию пересечения плоскости с поверхностью многогранника, необходимо по­строить линии пересечения плоскости с граня­ми. А это есть не что иное, как построение линии пересечения двух плоскостей: секущей плоскости с плоскостью грани. Для построения линии пересечение двух плоскостей, т. е. одной стороны многоугольника, достаточно построить две ее точки. Этими точками будут точки пере­сечения прямой с плоскостью, где прямая — ребро многогранника. Итак, построение линии пересечения многогранника с плоскостью сво­дится к нахождению точек пересечения ребер многогранника с секущей плоскостью. Затем эти точки соединяют отрезками и получают стороны многоугольника, лежащего в плоскости пересекающей многогранник.

Пересечение призмы проецирующей плоскостью

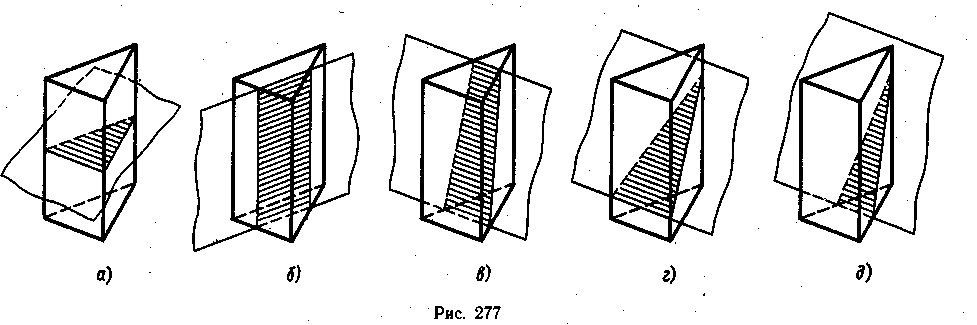
Форма линии пересечения зависит от формы призмы и от направления секущей плоскости. На рис. 277 показаны примеры пересечения треугольной призмы плоскостями различного положения.

Ортогональные проекции усеченной призмы

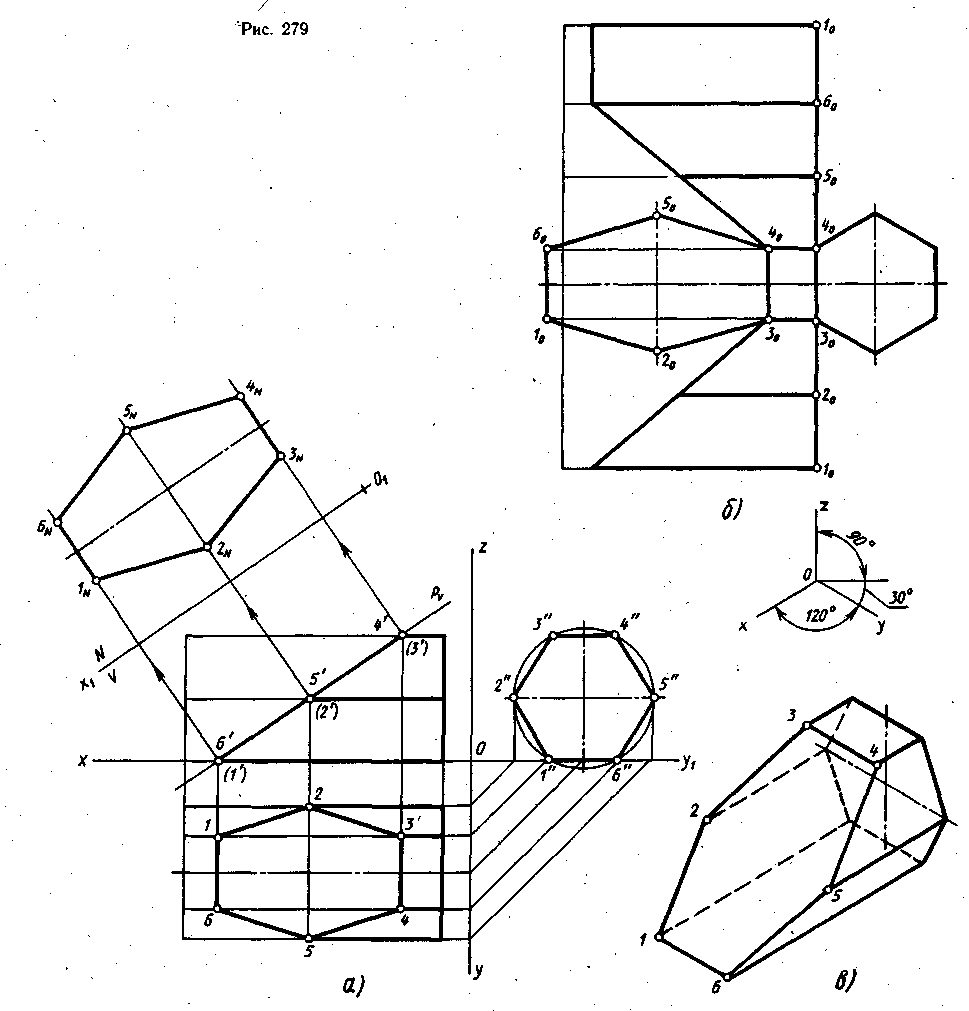
На рис. 278 изображена шестиугольная пра­вильная прямая призма, лежащая одной гра­нью на плоскости проекций Н. Основания призмы расположены параллельно плоскости проекций W. Призма пересечена фронтально-проецирующей плоскостью Р, которая задана следом Рѵ (рис. 279). Требуется построить ортогональные проекции усеченной призмы, натуральную величину фигуры среза, усечен­ную призму в изометрии и развертку боко­вой поверхности усеченной призмы. Будем считать, что плоскость Р отсекла левую часть призмы, которую на проекциях и развертке изобразим тонкими линиями. Оставшуюся (пра­вую) часть называют усеченной призмой и обво­дят сплошной основной линией.

Так как плоскость Р перпендикулярна плоско­сти проекции V, то она спроецируется на эту плоскость в прямую линию. На эту же линию спроецируется и фигура среза, лежащая в плоскости Р. Длина отрезка от точек 6'(1') до точек 4' (3') будет натуральной длиной фигуры среза. На профильной плоскости проекций боковые грани призмы проецируют­ся в отрезки, совпадающие со сторонами шестиугольника, лежащего в основании, а ребра боковой поверхности проецируются в точки, совпадающие с вершинами углов основа­ния. Фигура среза на профильной проекции совпадает с проекцией основания и изображает­ся как правильный шестиугольник, так как линии среза принадлежат боковым граням призмы, которые проецируются на профильную плоскость проекций отрезками. Отрезки 3-4, 2-5 и 1-6 проецируются на профильную плоскость проекции без искажения, так как они парал­лельны оси Оу, т. е. плоскости W. Значит на профильной проекции видна натуральная шири­на среза.

Н а горизонтальную плоскость проекций срез проецируется с искажением, так как плоскость Р, в которой лежит фигура среза, наклонена к плоскости проекций Н. Отрезки 13 и 64 проеци­руются с искажением. Отрезки 16, 25 и 34 па­раллельны оси Оу1 на профильной проекции, следовательно, параллельны плоскости Н, по­этому проецируются без искажения. Значит ширина среза и здесь спроецировалась в нату­ральную величину.

Ни на одной из трех плоскостей проекцій фигура среза не проецируется в натуральную величину, так как плоскость, в которой она ле­жит, не параллельна ни одной из плоскостей проекций. Для того чтобы построить ее нату­ральную величину, необходимо расположить фигуру среза параллельно какой-либо плоскос­ти проекции. На рис. 279, а это выполнено спо­собом перемены плоскостей проекций, где плос­кость Н заменена на плоскость N, параллельную плоскости Р. Для этого на фронтальной плоскости проекций параллельно фронтальному следу Рѵ плоскости Р на некотором расстоянии от него проведена новая ось О1х1. В этой системе плоскостей проекций плоскость Р, с лежащей в ней фигурой среза, расположена параллельно плоскости N, и новая проекция среза будет иметь натуральную величину.

Из точек 6', 2', 4' перпендикулярно оси О1х1 проводят линии проекционной связи, переносящие на плоскость N расстояния по длине среза. Затем от оси О1х1 откладывают отрезки, взятые с горизонтальной проекции призмы от оси Ох до точек 1...6, точки 1N...6N соединяют отрезками, получают нату­ральную величину среза.

Построение усеченной призмы в аксонометрии.

На рис. 279, в показана усеченная призма в изометрической проекции. Построение начина­ют с основания призмы. Проводят центровые линии основания в плоскости zOy параллельно осям Оу и Oz. Затем на центровой линии, па­раллельной оси Оу, откладывают отрезок 2-5, а на центровой линии, параллельной оси Oz,— расстояние между серединами сторон 3" 4" и 1" 6". Через точки, построенные на центровой линии, параллельной оси Oz, про­водят прямые (направление будущих сторон основания), параллельные оси Оу, и на них строят стороны основания, размер которых берут с профильной проекции. Концы построен­ных двух сторон соединяют отрезками с точка­ми, отложенными на центровой линии, парал­лельной оси Оу. Получили основание призмы. От вершины каждого угла основания, парал­лельно оси Оу проводят прямые, на которых откладывают соответствующие длины усечен­ных ребер, взятые с фронтальной или гори­зонтальной проекции. Построенные точки соединяют отрезками и получают фигуру сре­за.

Развертка поверхности усеченной призмы

Сначала проводят прямую, на которой от­кладывают шесть отрезков, равных стороне основания (ширина грани), размер отрезка берется с профильной проекции (рис. 279, б). Затем из полученных точек /о...6о проводят пря­мые,перпендикулярные этой прямой. На прове­денных перпендикулярах откладывают длины соответствующих усеченных ребер, которые измеряют на фронтальной или горизонтальной проекции. Построенные точки соединяют отрез­ками и получают ломаную линию среза. Затем пристраивают основание, а к одной из линий среза — натуральную величину среза.