
- •1.2. Матрицi
- •1.3. Вектори
- •1.4. Векторний простір
- •1.5. Множення матрицi на вектор
- •1.6. Елементарнi перетворення матриць
- •1.7. Матричне означення системи лiнiйних рiвнянь
- •1.8. Лiнiйне вiдображення, пов'язане з матрицею
- •2. Множення матриць, обернені матриці
- •2.1. Суперпозиція лінійних відображень
- •2.2. Розбиття матрицi на рядки I стовпчики та множення матриць
- •2.3. Множення на елементарнi матрицi
- •2.4. Обернені матриці
- •2.4.1. Як знайти обернену матрицю?
- •2.4.2. Як розкласти оборотну матрицю в добуток елементарних?
- •2.4.3. Способи зведення матриці до одиничної
- •2.5. Задачі для самостійного розв'язання
- •3. Ранги
- •3.1. Лiнiйна залежнiсть векторiв
- •3.2. Абстрактний векторний простiр
- •3.3. Ранг системи векторiв
- •3.4. Ранг матрицi
- •3.5. Поняття лiнiйної оболонки
- •3.6. Розв'язування систем лінійних рівнянь
- •3.7. Методика розв'язування задач
- •3.8. Задачі для самостійного розв'язання
- •4. Визначник
- •4.1. Функція визначника
- •4.2. Обчислення визначника за методом Гаусса
- •4.3. Пiдстановки та перестановки
- •4.4. Формула для обчислення визначника
- •4.5. Мiнори
- •4.6. Задачі для самостійного розв'язання
- •Відповіді на задачі для самостійного розв'язання
- •Рекомендована лiтература
- •1.1. Вступ
2.5. Задачі для самостійного розв'язання
Знайдіть обернені до матриць
1.
![]() 2.
2.
![]() 3.
3.
 4.
4.
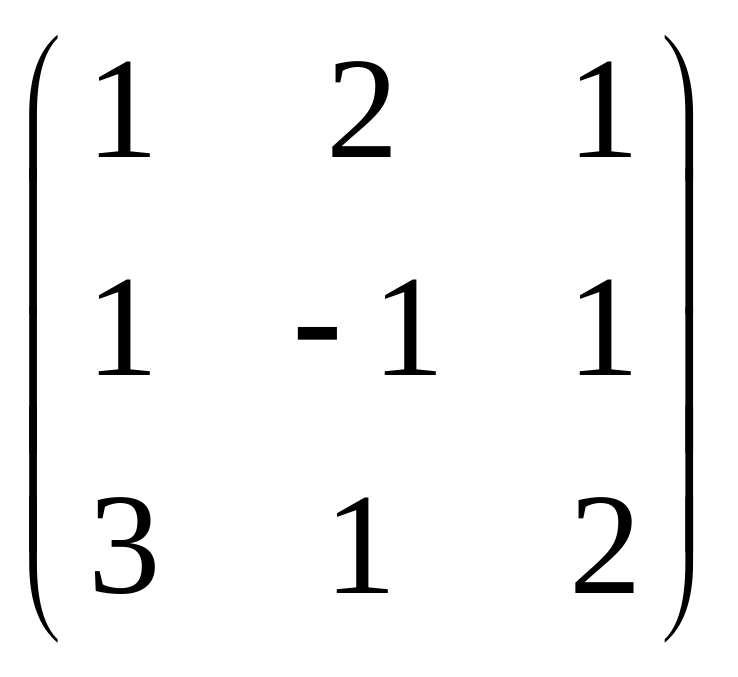
![]()
5.
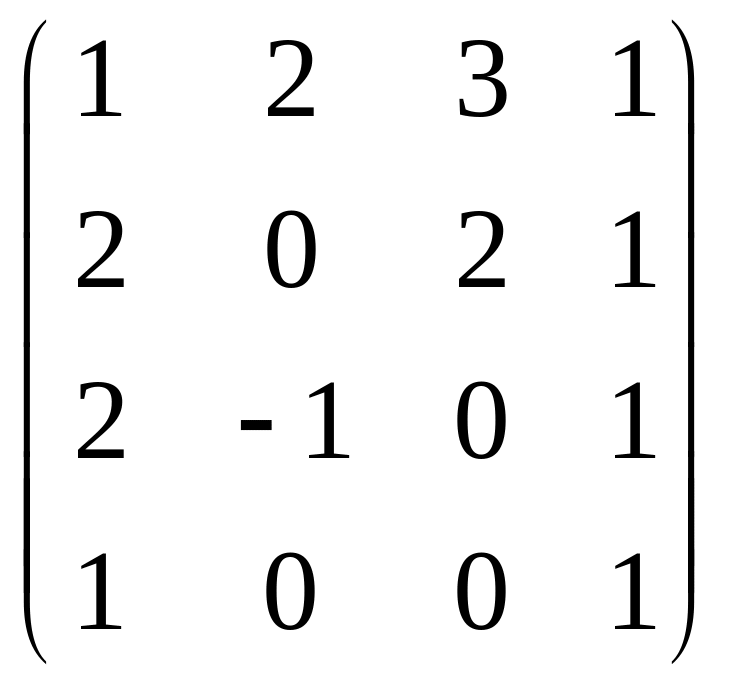 6.
6.
 7.
7.
 .
.
3. Ранги
3.1. Лiнiйна залежнiсть векторiв
Означення.
Зафiксуємо
деяке число
![]() .
Лiнiйною комбiнацiєю векторiв
.
Лiнiйною комбiнацiєю векторiв
![]() з коефiцiєнтами
з коефiцiєнтами
![]()
![]() називається вектор вигляду
називається вектор вигляду
![]()
![]()
![]() де
де
![]() –
деякi числа (з
).
–
деякi числа (з
).
Скiнченна
послiдовнiсть, або набiр векторiв однакового
розмiру
![]()
![]() називається системою
векторiв.
Iнодi
використовують позначення
називається системою
векторiв.
Iнодi
використовують позначення
![]() ,
де
,
де
![]() .
.
Нехай
![]() –
деяка система векторiв. Система векторiв
називається лiнiйно
залежною,
якщо iснує набiр
чисел
–
деяка система векторiв. Система векторiв
називається лiнiйно
залежною,
якщо iснує набiр
чисел
![]() ,
серед яких є щонайменше одне відмінне
0, таких, що
,
серед яких є щонайменше одне відмінне
0, таких, що
![]() .
.
Система
векторiв
називається лiнiйно
незалежною,
якщо для довiльного набору з
чисел
рiвнiсть
має мiсце тiльки тодi, коли
![]()
![]()
![]()
![]() .
.
Зауваження. Лiнiйна комбiнацiя, що дорівнює нулю, iснує завжди – коли всi коефiцiєнти дорiвнюють нулю. У визначеннi лiнiйної залежностi хоча б один з коефiцiєнтiв не рiвний нулю!
Означення.
Нехай
![]() деяка система векторiв. Ненульовий
вектор-стовпчик
деяка система векторiв. Ненульовий
вектор-стовпчик
![]() разом зi спiввiдношенням
разом зi спiввiдношенням
![]() називається лiнiйною залежнiстю мiж
векторами
називається лiнiйною залежнiстю мiж
векторами
![]() .
.
Приклади.
1. Припустимо, що система складається з
двох векторiв
![]() ,
таких, що
,
таких, що
![]() .
Тодi ця система є лiнiйно залежною. Дiйсно,
покладемо
.
Тодi ця система є лiнiйно залежною. Дiйсно,
покладемо
![]()
![]() Тодi
Тодi
![]()
![]() .
.
2.
Деяке узагальнення попереднього
прикладу. Припустимо, що система
мiстить два рiвні вектори
![]() ,
.
Тодi ця система є лiнiйно залежною. Якщо
покладемо
,
.
Тодi ця система є лiнiйно залежною. Якщо
покладемо
![]() ,
,
![]() ,
,
![]() для всiх iнших
для всiх iнших
![]() ,
то
,
то
![]() .
.
3.
Припустимо, що система складається з
одного вектора
![]() Перевiрте (це просто), що ця система буде
лiнiйно незалежною, коли
Перевiрте (це просто), що ця система буде
лiнiйно незалежною, коли
![]() та лiнiйно залежною, коли
та лiнiйно залежною, коли
![]() .
.
Отже,
система
![]() є лiнiйно незалежною, а система
є лiнiйно незалежною, а система
![]() – лiнiйно залежною.
– лiнiйно залежною.
4. Система векторiв, що мiстить нульовий вектор, завжди лiнiйно залежна.
Покажіть це.
Означимо
в
-вимірному
числовому просторі
вектори
![]() :
:![]() є такий вектор з
,
у якого всi координати, крiм
-тої,
дорiвнюють нулю, а
-та
координата дорiвнює
.
Через
є такий вектор з
,
у якого всi координати, крiм
-тої,
дорiвнюють нулю, а
-та
координата дорiвнює
.
Через
![]() позначається символ
Кронекера. Вiн залежить
вiд двох iндексiв
та
і визначається формулою:
позначається символ
Кронекера. Вiн залежить
вiд двох iндексiв
та
і визначається формулою:
![]() .
.
Наприклад,
![]()
![]()
![]() Використовуючи символ Кронекера, можемо
записати формулу для координат вектора
Використовуючи символ Кронекера, можемо
записати формулу для координат вектора
![]()
![]() ,
,
![]() .
.
Задачa.
Довести, що система векторiв
![]() для довiльного
для довiльного
![]() є лiнiйно незалежною.
є лiнiйно незалежною.
Розв'язання.
Припустимо, що
![]() .
Але тоді
.
Але тоді
![]()
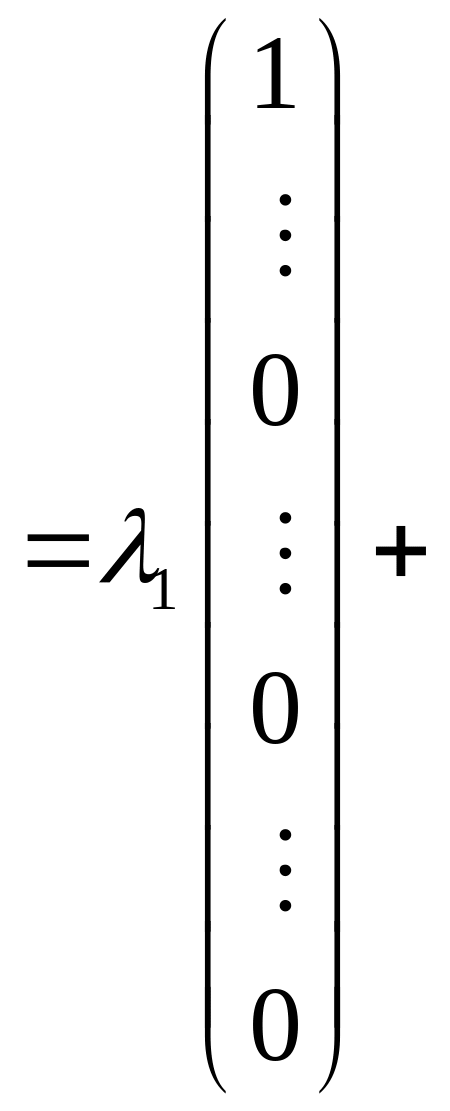

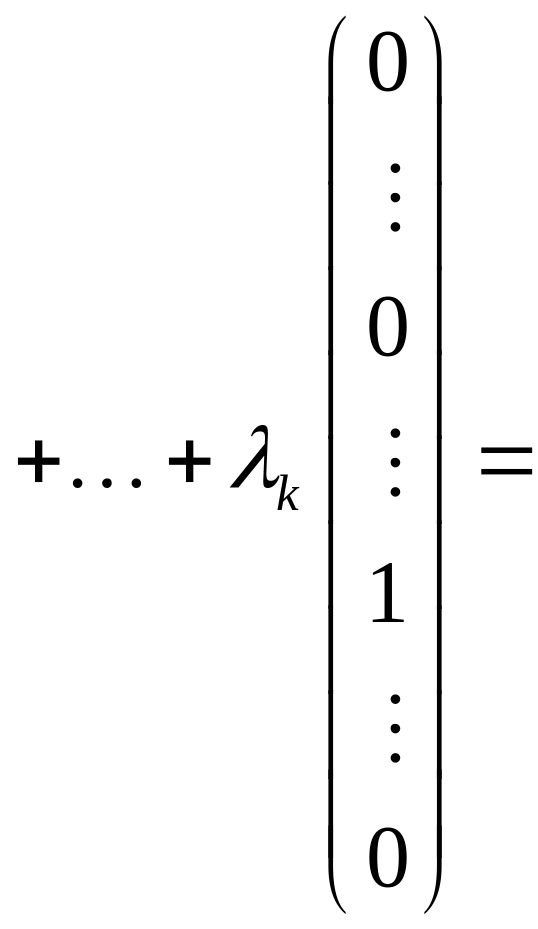
![]()
![]() .
.
Оскiльки
у рiвних векторiв однойменнi координати
дорівнюють одна одній, одержуємо
![]()
![]()
![]() .
.
Приклад.
Нехай заданi
векторiв
![]() розмiрностi
.
Як перевiрити, чи є вони лiнiйно залежними?
Як знайти всi лiнiйнi залежностi мiж цими
векторами?
розмiрностi
.
Як перевiрити, чи є вони лiнiйно залежними?
Як знайти всi лiнiйнi залежностi мiж цими
векторами?
Розв'язання. Щоб розв'язати цю задачу, запишемо вектори як вектори-стовпчики:
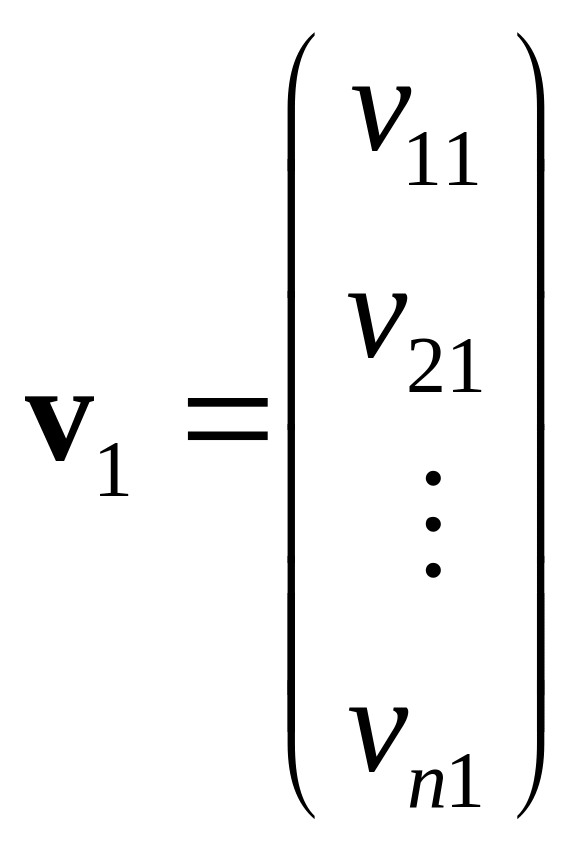 ,
, ,
,
![]() ,
,
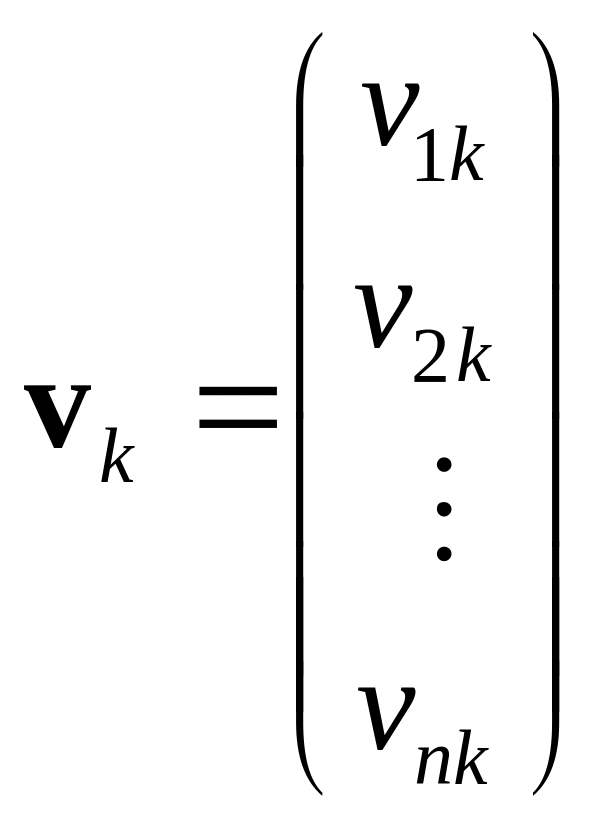 .
.
Перший iндекс у цьому запису означає номер координати, а другий – позначає номер вiдповiдного вектора.
Запишемо
умову
![]() ,
використовуючи координати векторiв:
,
використовуючи координати векторiв:


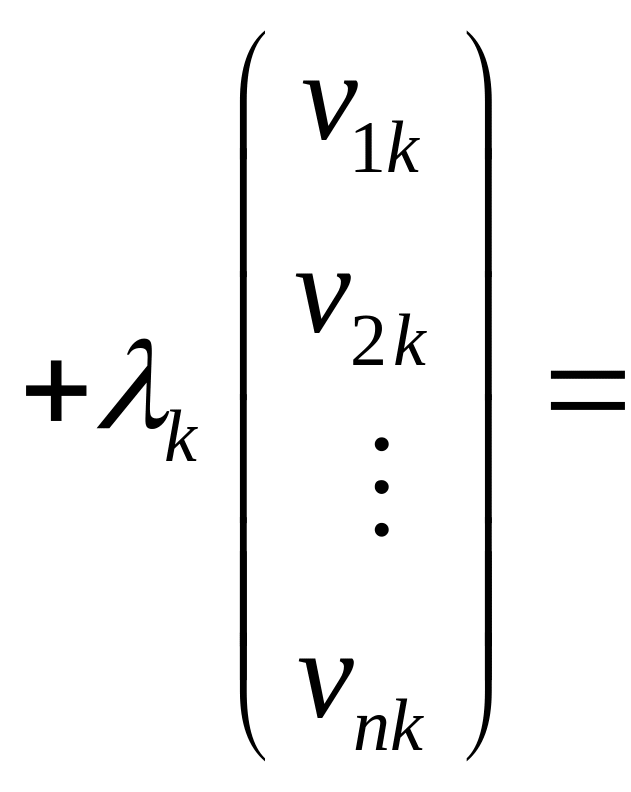
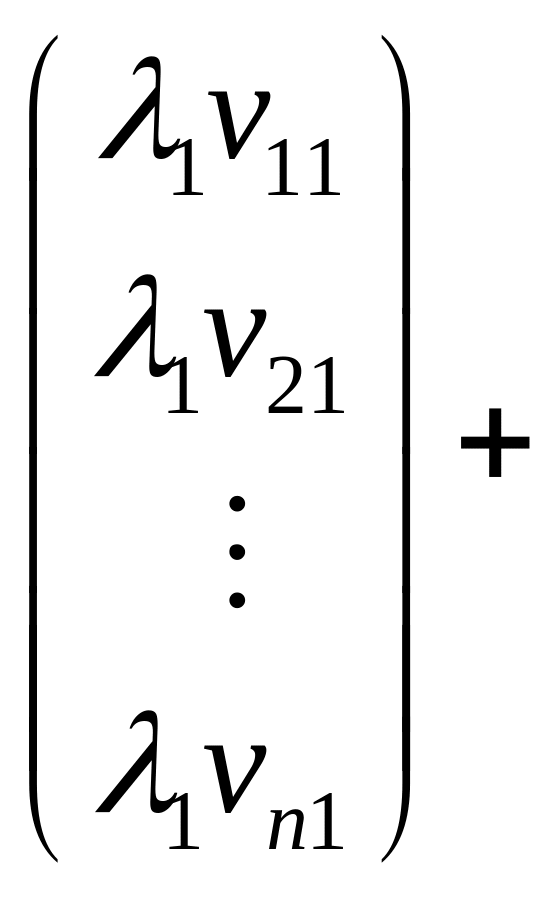
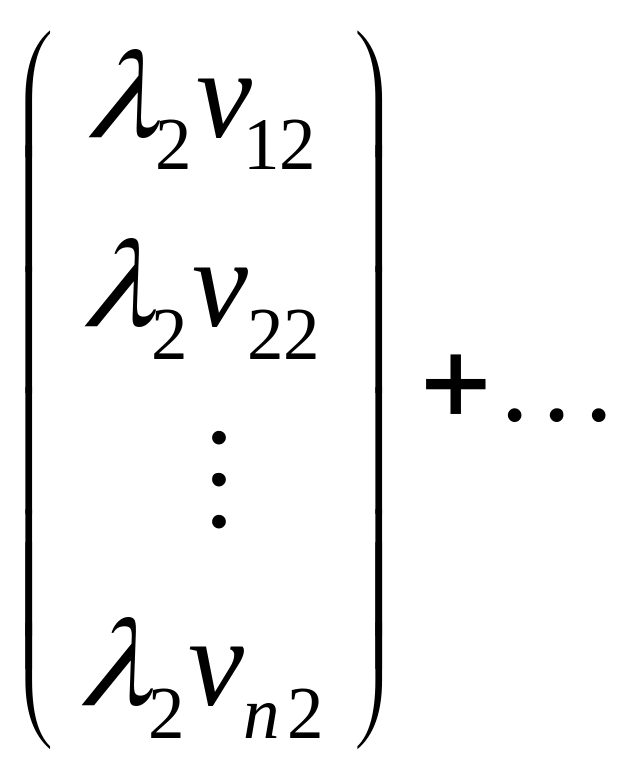
 .
.
![]()
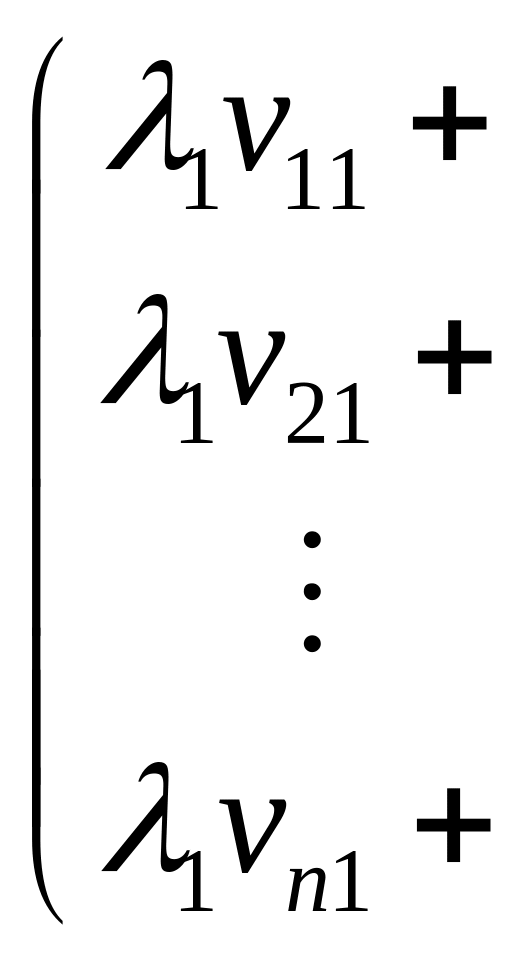

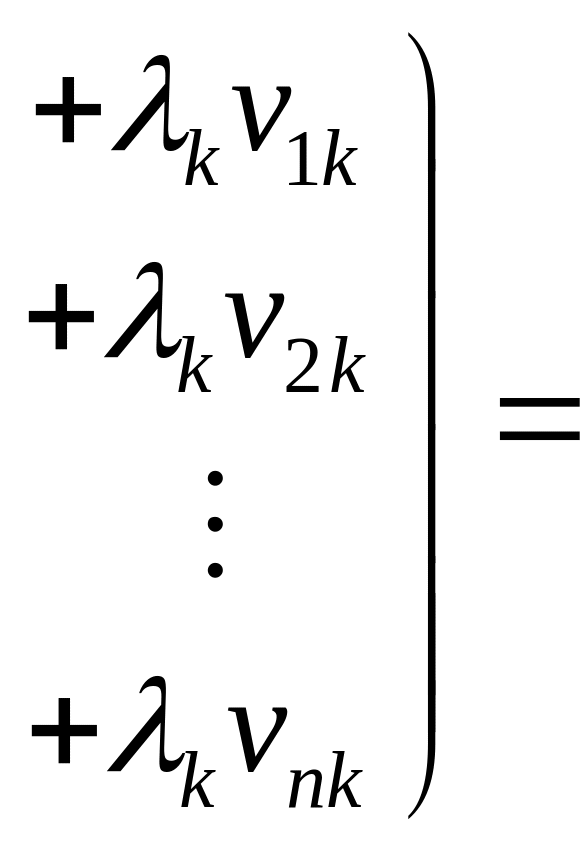
![]() .
.
Два вектори рiвнi тодi i тiльки тодi, коли рiвнi їх однойменнi координати. Тому останню рiвнiсть переписуємо як систему лiнiйних рiвнянь вiдносно невiдомих :

 (3)
(3)
Наведенi вище мiркування дозволяють сформулювати таке правило.
Правило. Система векторiв є лiнiйно залежною тодi i тiльки тодi, коли система лiнiйних рiвнянь (3) має ненульовий розв'язок. Знайти всi лiнiйнi залежностi мiж векторами означає: знайти всi ненульовi розв'язки системи (3).
Розширена
матриця
![]() системи (3) одержується так: її першi
стовпчикiв збiгаються з векторами-стовпчиками
системи (3) одержується так: її першi
стовпчикiв збiгаються з векторами-стовпчиками
![]()
![]() ,
а останнiй стовпчик є нульовим, тобто
,
а останнiй стовпчик є нульовим, тобто
![]()
![]() .
.
Нагадаємо,
що в однорiднiй системi рiвнянь нульовий
стовпчик правих частин для спрощення
не пишеться. Тому розглядаємо в наступному
прикладi тiльки матрицю системи
![]() ,
а не розширену матрицю системи.
,
а не розширену матрицю системи.
Задачa. Знайти всi лiнiйнi залежностi мiж векторами
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Розв'язання. Згдіно з наведеним вище правилом, для знаходження всiх лiнiйних залежностей мiж указаними векторами необхiдно знайти всi ненульовi розв'зки однорiдної системи з матрицею
![]() .
.
Систему розв'язуємо за допомогою методу Гаусса:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Отже,
одержаний розв'язок буде:
![]()
![]()
![]()
![]()
![]() Лiнiйнiй залежностi вiдповiдає будь-який
ненульовий розв'язок.
Лiнiйнiй залежностi вiдповiдає будь-який
ненульовий розв'язок.
Вiдповiдь.
Коефiцiєнти
лiнiйної залежностi визначається так:
![]()
![]() є довiльними, такими, що не дорівнюють
одночасно нулю,
Наприклад, поклавши
є довiльними, такими, що не дорівнюють
одночасно нулю,
Наприклад, поклавши
![]() ,
,
![]() ,
одержимо
,
одержимо
![]() ,
,
![]() ,
а отже, маємо лінійну залежність:
,
а отже, маємо лінійну залежність:
![]() .
.
Укажемо на зв'язок між множенням матрицi на вектор та лiнiйними комбiнацiями.
Припустимо,
що матриця
![]() зображена у виглядi
векторiв-стовпчикiв. Тодi утворити лiнiйну
комбiнацiю цих векторiв
зображена у виглядi
векторiв-стовпчикiв. Тодi утворити лiнiйну
комбiнацiю цих векторiв
![]() з коефiцiєнтами
з коефiцiєнтами
![]() –
це те саме, що помножити матрицю
справа на вектор
–
це те саме, що помножити матрицю
справа на вектор
 :
:
![]() .
.
Нехай
матриця
![]() зображена як об'єднання своїх рядкiв.
Тодi утворити лiнiйну комбiнацiю цих
векторiв
зображена як об'єднання своїх рядкiв.
Тодi утворити лiнiйну комбiнацiю цих
векторiв
![]() з коефiцiєнтами
з коефiцiєнтами
![]() –
це те саме, що помножити матрицю
зліва на вектор
–
це те саме, що помножити матрицю
зліва на вектор
![]() :
:
![]() .
.
