1.7. Матричне означення системи лiнiйних рiвнянь

Позначимо через вектор-стовпчик висоти , -тою координатою якого є невiдоме , тобто . Тодi за формулою , де – -та координата, можна формально означити добуток матрицi на вектор-стовпчик невiдомих . У цьому випадку систему лiнiйних рiвнянь (1) перепишеться у виглядi

де є вектор-стовпчик, складений з правих частин.

Розв'язок системи  – це такий вектор , для якого виконується . Розв'язати систему рiвнянь означає: знайти всi розв'язки цiєї системи або ж показати, що таких розв'язкiв немає.

Позначимо через нульовий вектор-стовпчик. Тодi однорiдна система лiнiйних рiвнянь запишеться у виглядi

Твердження. Множина розв'язкiв системи не змiниться, якщо виконуватимуться елементарні перетворення над рядками розширеної матриці системи

.

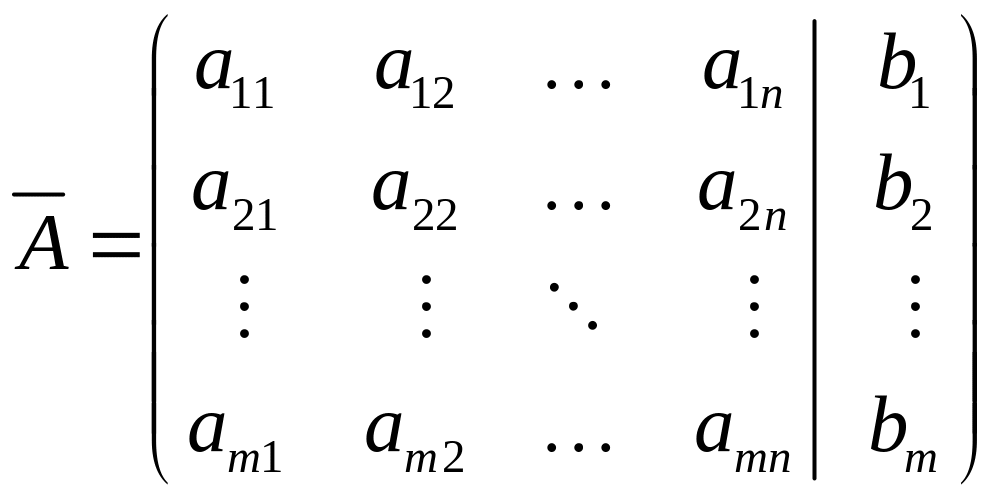Метод Гаусcа розв'язування систем лінійних рівнянь полягає в тому, що елементарними перетвореннями рядків розширена матриця системи зводиться до найпростішого східчастого вигляду. Після цього розв'язок системи виписується просто.

1.8. Лiнiйне вiдображення, пов'язане з матрицею

Кожна матриця розмiру визначає вiдображення з -вимiрного простору в -вимiрний, при якому вектор переходить в У цьому разі пишуть також . Ще один еквiвалентний спосiб запису .

Властивостi вiдображення . Вiдображення є лiнiйним. Це означає, що для довільних , виконуються рівності

.

Одиничній -матриці відповідає тотожне відображення , при якому .

Образом вектора відносно лінійного відображення є вектор . Множина образів усіх векторів називається образом лінійного оператора .

Прообразом вектора відносно лінійного відображення назива-ється довільний вектор такий, що . Множина всіх прообразів вектора утворює його повний прообраз, який позначається :

.

Повниий прообраз нульового вектора називається ядром лінійного відображення, яке позначається .

Задачa. Нехай – лiнiйне вiдображення, що визначається за допомогою матрицi . Чому дорiвнює образ вектора ?

Розв'язання. За визначенням, образ вектора обчислюється як

.

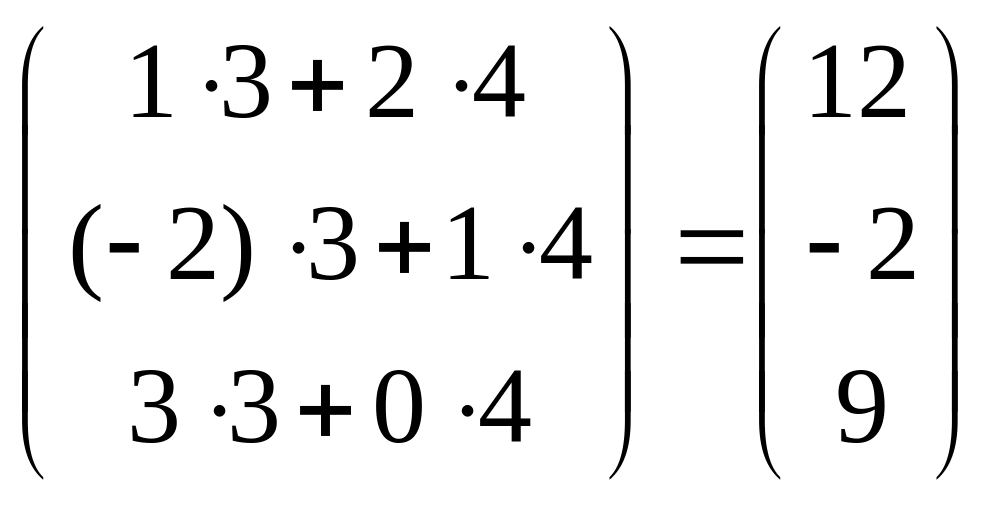Вiдповiдь. Образом вектора є вектор .

Правило. Якщо є лiнiйне вiдображення, визначене за допомогою матрицi , то знайти прообраз вектора :

1) є те саме, що знайти всi вектори , для яких ;

2) або ж те саме, що знайти всi , для яких ;

3) або ж те саме, що розв'язати систему лiнiйних рiвнянь

з розширеною матрицею .

Приклад. Нехай є те саме лiнiйне вiдображення, що й у попередньому прикладі. Завдання: знайти прообраз вектора .

Згідно з правилом, знайти прообраз вектора вiдносно вiдображення з матрицею – це те саме, що розв'язати лiнiйну систему з розширеною матрицею

.

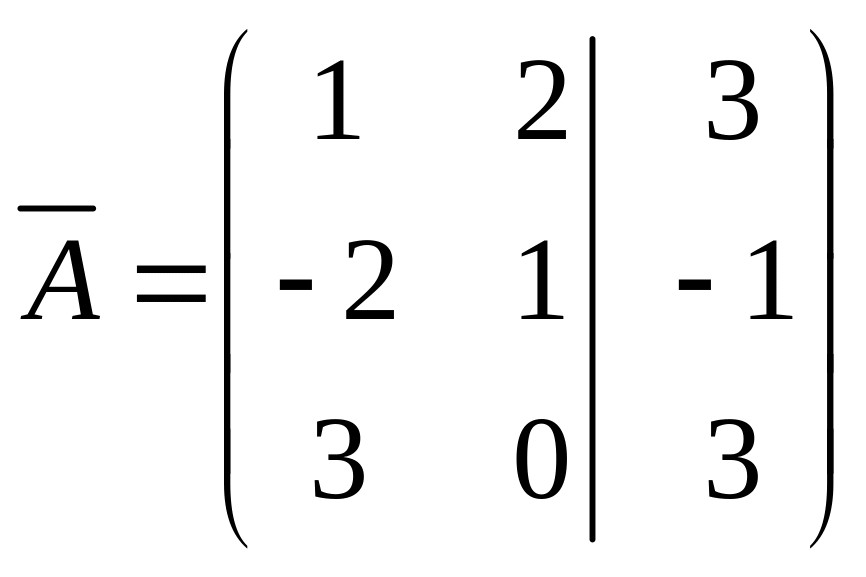Розв'язуємо цю систему методом Гаусса.

.

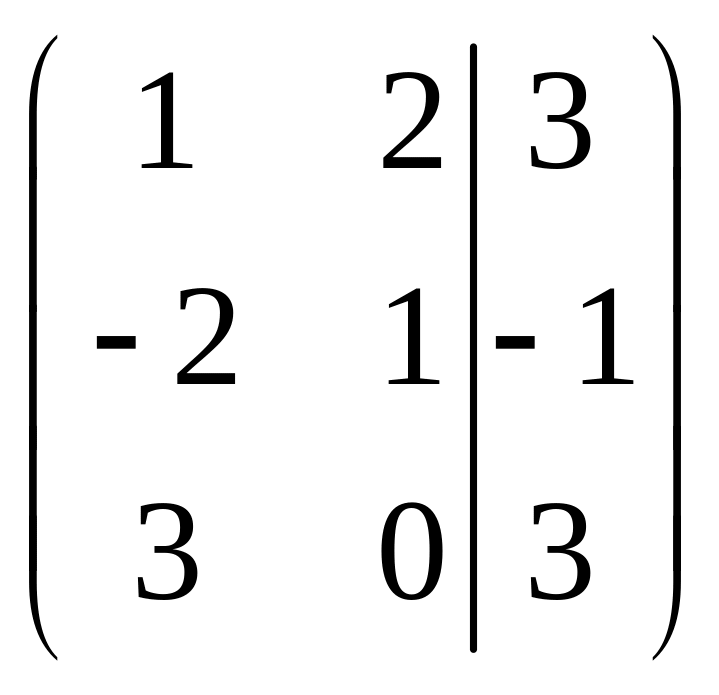
Вiдповiдь. Прообраз вектора дорiвнює .

Зауваження. Задача пошуку прообразу повнiстю еквiвалентна задачi розв'язування системи лiнiйних рiвнянь, тому прообрази поводять себе як розв'язки вiдповiдної лiнiйної системи. Отже, можливi такi варiанти:

1. Вектор має один прообраз (вiдповiдна система визначена).

2. Вектор має нескiнченно багато прообразiв (вiдповiдна система сумiсна, але невизначена).

3. Вектор не має прообразiв (вiдповiдна система несумiсна).