Київський національний університет імені Тараса Шевченка

С.А.Овсієнко

В.С.Мазорчук

Н.С.Головащук

ЛІНІЙНА АЛГЕБРА

МАТРИЦІ Й ДЕТЕРМІНАНТИ

Навчальний посібник

Київ - 2001



1. Загальнi факти про матриці та вектори

1.1. Вступ

Зi шкiльної математики вiдомо, що вектори з початком у вибранiй точцi простору можна множити на дiйсне число та додавати за правилом паралелограма. Це найперший і найпростiший приклад лiнiйного простору, який ще прийнято називати векторним. Оголосивши основнi властивостi цих векторiв аксiомами та замiнивши тривимiрнiсть -вимiрнiстю, приходимо до загального означення -вимiрного числового лiнійного простору.

У стандартному фiзичному векторному просторi можливi вiдображення векторiв – наприклад, зсуву або повороту – якi переводять один такий векторний простiр в iнший. У випадку лiнiйних просторiв одержимо узагальнююче поняття лiнiйного оператора, або лiнiйного вiдображення, якi постулюються також деякими аксiомами.

Предметом вивчення лiнiйної алгебри є, в основному, лiнiйнi простори та лiнiйнi вiдображення, а основним засобом є застосування матриць та векторів.

1.2. Матрицi

Означення. Матрицею з рядками та стовпчиками називається прямокутна числова таблиця

Числа називаються елементами матрицi.

Таку матрицю називають також  – матрицею або матрицею розмiру . Вона мiстить елементiв. У випадку матриця називається квадратною.

Указану вище матрицю iнколи записують у виглядi

Цей запис цiлком еквiвалентний попередньому.

Кажуть, що на -тому мiсцi в матрицi знаходиться -тий елемент , який ще називають елементом з iндексом або чи , де перший iндекс вказує номер рядка, а другий iндекс указує номер стовпчика, в якому знаходиться цей елемент. Елементи матриці , в яких обидва iндекси збiгаються, називаються дiагональними елементами матрицi .

Двi матрицi

та

розмiру називаються рiвними тодi i тiльки тодi, коли вони дорівнюють один одному поелементно, тобто для довiльних двох iндексiв виконується .

Укажемо деякi спецiальнi матрицi та вектори.

Для кожної пари натуральних чисел i iснує нульова матриця. Нульовою матрицею (розмiру ) назвемо матрицю , усi елементи якої дорiвнюють нулю:

.

Нульова матриця часто позначається просто . Цiкавішою є одинична матриця, яка завжди квадратна. Спочатку визначимо дiагональ квадратної матрицi.

Дiагоналлю (або головною дiагоналлю) квадратної матрицi , , називається послiдовнiсть усiх дiагональних елементiв цiєї матрицi.

Одинична матриця – це така квадратна матриця , у якої всi дiагональнi елементи дорiвнюють одиницi, а решта – нулю: , , .

Для кожного натурального iснує одинична матриця розмiру

Дiагональна матриця – це така квадратна матриця , у якої всi недiагональнi елементи дорiвнюють нулю: , якщо ; .

Кожна одинична матриця є, звичайно, дiагональною матрицею. Зворотне твердження неправильне. Нульова квадратна матриця є дiагональною.

1.3. Вектори

Матрицi розмiру та видiляються окремо i називаються вiдповідно векторами-рядками та векторами-стовпчиками. Наведемо незалежне означення.

Означення. Упорядкований набiр з чисел, записаних у стовпчик , називається вектором-стовпчиком висоти . Упорядкований набiр з чисел, записаних у рядок , називається вектором-рядком довжини .

Елементи вектора називають координатами. У вектора-рядка , елемент , що знаходиться на -тому мiсцi, називається -тою координатою вектора . Аналогiчно у вектора-cтовпчика

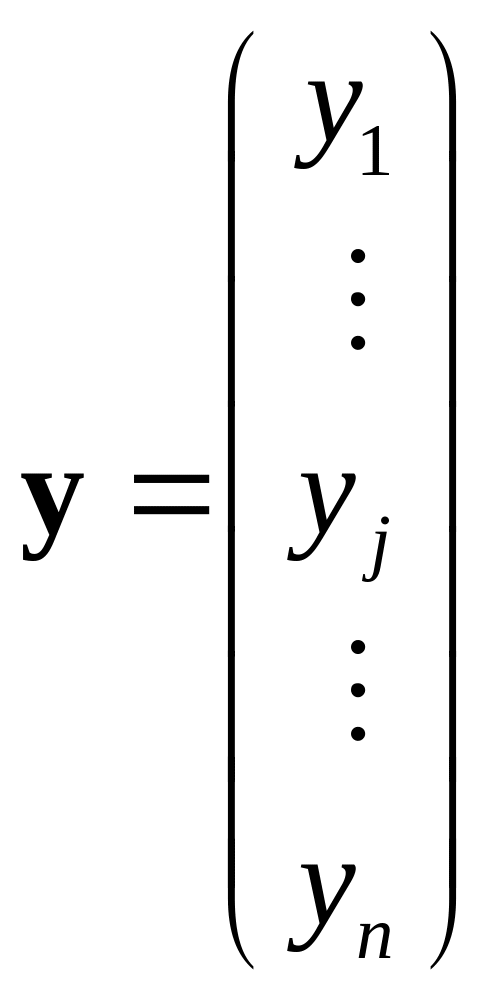
елемент , що знаходиться на -тому мiсцi, називається -тою координатою вектора .

Так само, як i матрицi, два вектори-рядки (або два вектори-стовпчики) вважаються рiвними, якшо вони рiвнi покоординатно.

Довiльну матрицю , , можна розглядати як складену з векторiв-рядкiв довжини :

.

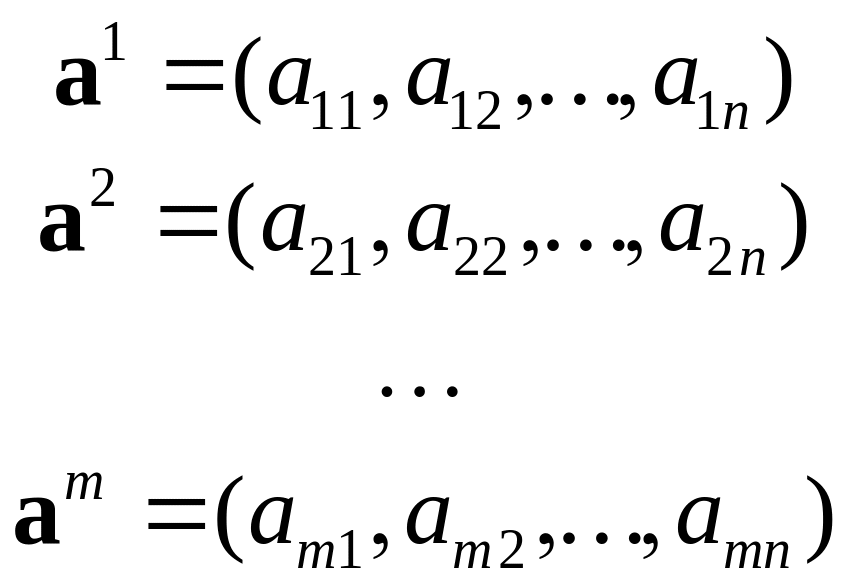
Горизонтальнi риски в указаному запису матрицi вiддiляють рядки один вiд одного, але інколи ми їх не писатимемо.

Аналогiчно, матрицю можна розглядати як складену з векторiв-стовпчикiв висоти :

, , … ,

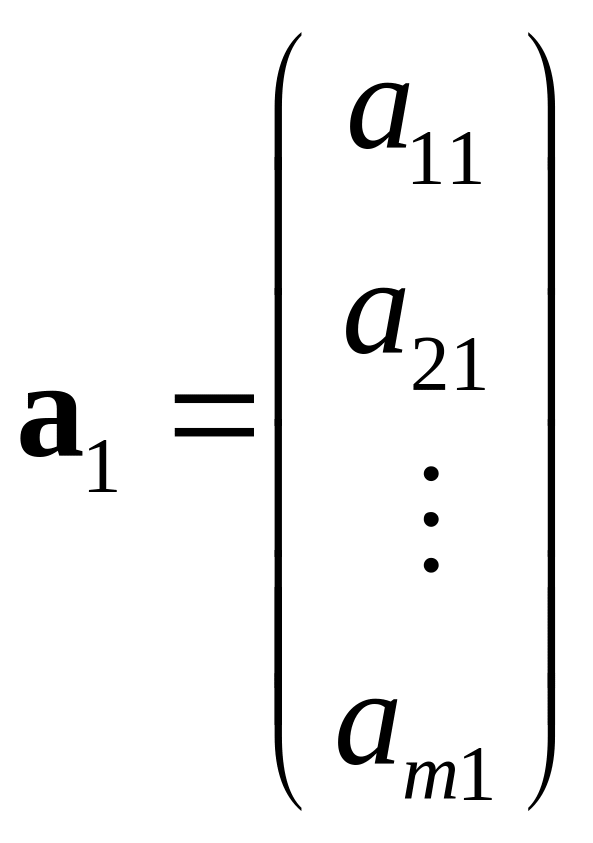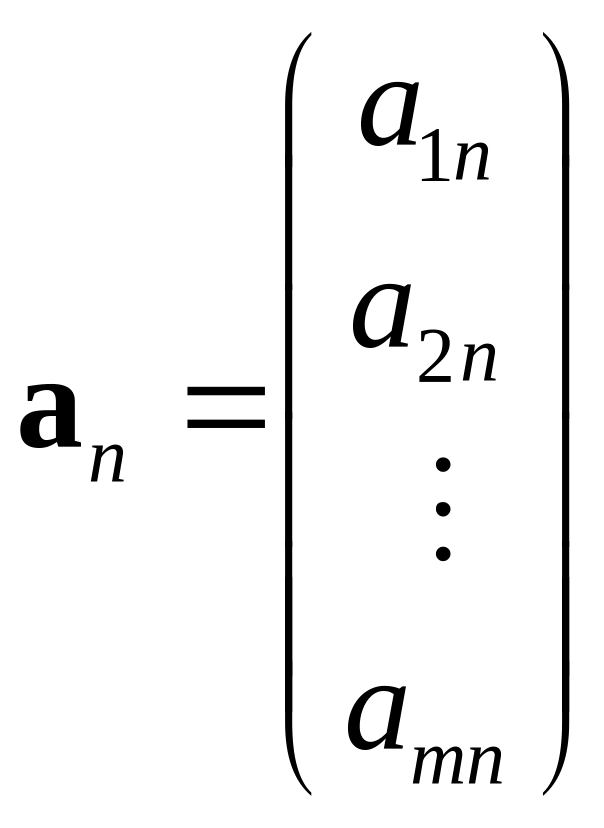
Вертикальнi риски у вказаному запису матрицi вiддiляють стовпчики один вiд одного.