
- •Індивідуальні завдання за темою:
- •Завдання 1
- •19) Побудуйте точки, що зображують комплексні числа з модулем рівним 1, аргументи яких дорівнюють: . Доведіть, що сума цих чисел дорівнює нулю.
- •23) Надайте в алгебраїчній формі числа:
- •Завдання 2
- •Завдання 3
- •Індивідуальні завдання за темою: «Лінійна алгебра» Завдання №1
- •Завдання №2
- •Індивідуальні завдання за темою: «Елементи векторної алгебри та аналітичної геометрії»
- •Варіанти
- •Завдання №2
- •Індивідуальні завдання за темою: «Диференціальне числення функції однієї змінної»
- •Завдання №1
- •Завдання №2
- •Завдання №3
- •Завдання №4
- •Завдання №5
- •Завдання №6
- •Завдання №7
- •Завдання № 8
- •Завдання 9
- •Індивідуальні завдання за темою «Невизначений інтеграл та визначений інтеграл»
- •Індивідуальні завдання за темою Диференціальне числення функцій багатьох змінних
- •Індивідуальні завдання за темою за темою «Числові та функціональні ряди. Ряди Фур’є»
- •Індивідуальні завдання за темою Векторний аналіз Завдання №1
- •Завдання № 2
- •Завдання № 3
- •Завдання № 4
- •Індивідуальні завдання за темою Диференціальні рівняння та системи диференціальних рівнянь
- •Індивідуальні завдання за темою
- •Індивідуальні завдання за темою
- •Індивідуальні завдання за темою «Випадкові події та ймовірність» Завдання 1.
- •Завдання 2.
- •Завдання 3
- •Завдання 4
- •Завдання 5
- •Індивідуальні завдання за темою «Випадкові величини їх закони розподілу» Завдання 1.
- •Завдання 2
- •Література
Міністерство освіти та науки, молоді та спорту України
Одеська державна академія технічного регулювання та якості
Кафедра загальнотехнічних та фундаментальних дисциплін
Вища математика
Збірник завдань до виконання
розрахунково-графічних
робіт
для студентів 1-3 курсів
Одеса
2012 р.
Укладачі: кандидат технічних наук, доцент Зборовська І.А.
старший викладач Лінкова О.В.
оформлення Лубманенко В.Б., Лебзяк В.Л.
Методичний посібник призначений для студентів всіх форм навчання, та містить варіанти розрахунково–графічних робіт з усіх тем навчальної програми з дисципліни “Вища математика”. Посібник відповідає сучасним методам контролю знань студентів.
Виконанння розрахунково-графічних робіт допомогає студенту підготуватися до здачі заліку та екзамену з цієї дисципліни.
Індивідуальні завдання за темою:
”КОМПЛЕКСНІ ЧИСЛА”
Завдання 1
1)
Що означає кожне з наступних тверджень:
а) комплексне число
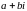 дорівнює нулю;
б) комплексне число
не дорівнює нулю?
дорівнює нулю;
б) комплексне число
не дорівнює нулю?
2)
Що означає кожне з наступних тверджень:
а) комплексні числа
та
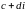 дорівнюють одне одному; б) комплексні
числа
та
не дорівнюють одне одному?
дорівнюють одне одному; б) комплексні
числа
та
не дорівнюють одне одному?
3) Чи можуть бути спряженими: а) два дійсних числа; б) дійсне та уявне число; два суто уявних числа?
4)
Яке число є спряженим до числа
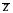 ?
?
5) При якій умові сума двох комплексних чисел є: а) дійсне число; б) суто уявне число?
6) Що можна сказати про два комплексних числа, якщо сума та різниця одночасно уявляють собою: а) деяке число; б) суто уявне число?
7) Наведіть приклади комплексних чисел та дій над ними, результат яких є дійсне число.
8) Чи може сума квадратів двох комплексних чисел бути від’ємною?
9)
Чи може квадратне рівняння з дійсними
коефіцієнтами мати корені
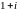 та
та
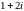 ?
?
10)
В якій чверті координатної площини
розташовані точки, що відображують
числа
 ?
?
11) Що можна сказати про комплексні числа, для яких відповідні точки розташовані на прямій, паралельній: а) вісі ОХ4 б) вісі ОУ ?
12)
Що можна сказати про модулі двох спряжених
комплексних чисел? Знайдіть модулі
чисел
 ?
?
13) Чому дорівнює аргумент: а) суто уявного числа; б) будь-якого від’ємного числа; в) будь-якого додатного числа; г) нуля ?
14)
Які знаки мають числа а та b, якщо аргумент
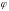 комплексного числа
задовільняє умові: а)
комплексного числа
задовільняє умові: а)
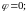 б)
б)
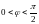 ;
в
;
в
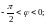 г)
г)
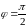
15)
Нехай
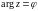 .
Чому дорівнює
.
Чому дорівнює
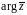 ,
,
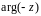 ?
?
16) В яких границях міститься головне значення аргументу комплексного числа, що розташоване у: а) першій чверті; б) другій чверті?
17) В яких границях міститься головне значення аргументу комплексного числа, що розташоване у: а) третій чверті; б) четвертій чверті?
18)
Побудуйте точки, що зображують комплексні
числа з модулем рівним 1, аргументи яких
дорівнюють:
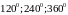 .
Доведіть, що сума цих чисел дорівнює
нулю.
.
Доведіть, що сума цих чисел дорівнює
нулю.
19) Побудуйте точки, що зображують комплексні числа з модулем рівним 1, аргументи яких дорівнюють: . Доведіть, що сума цих чисел дорівнює нулю.
20) На площині дано коло з центр у початку координат та радіусом, що дорівнює 5. При якій умові точка, яка зображує комплексне число z буде лежати: а) в середині кола; б) на колі?
21) На площині дано коло з центром у початку координат та радіусом, що дорівнює 5. При якій умові точка, яка зображує комплексне число z буде лежати: а) поза колом; б) у центрі кола ?
22)
Надайте в алгебраїчній формі числа:
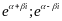
23) Надайте в алгебраїчній формі числа:
24) На площині дано коло з центром у початку координат та радіусом, що дорівнює 2. При якій умові точка, яка зображує комплексне число z буде лежати: а) поза колом; б) у центрі кола ?
25) В яких границях міститься головне значення аргументу комплексного числа, що розташоване у: а) другій чверті; б) третій чверті?
26) В який спосіб виконується множення комплексних чисел, заданих у показниковій формі?
27) В який спосіб виконується піднесення до натурального степеня комплексного числа, заданого у показниковій формі?
28) В який спосіб виконується ділення комплексних чисел, заданих у показниковій формі?
29) В який спосіб здобувається корінь степеня n, де n є N з комплексного числа, заданого у показниковій формі?
30) В який спосіб виконується додавання комплексних чисел, заданих у векторній формі?
