1.3.7. Выводы

1. С ростом тока I в обмотке ЭМ магнитная индукция B_ в рабочем зазоре увеличивается.

2. Рост тока I не приводит к перераспределению потока _ в рабочем воздушном зазоре и потока рассеяния _рас ЭМ.

3. При увеличении тока I материал магнитопровода может войти в зону насыщения (пологий участок основной кривой намагничивания). Это существенно увеличивает магнитное напряжение на магнитопроводе, снижает долю МДС М обмотки ЭМ, затрачиваемую на создание индукции B_, и, как следствие, снижает эффективность намагничивающей обмотки ЭМ.

Тема 2. Построение математической модели дифференциального трансформаторного индуктивного преобразователя прямоходного типа

2.1. Описание моделируемого объекта

Моделируемый дифференциальный трансформаторный индуктивный преобразователь прямоходного типа (далее «ДТИП») схематически изображен на рис. 2.1. ДТИП состоит из подвижного цилиндрического магнитного якоря 1, перемещающегося внутри электроизоляционного (пластикового) каркаса 6 катушки в направлении оси его симметрии. На каркасе катушки равномерно размещена первичная обмотка (обмотка возбуждения) 3 с числом витков N₁, разбитая на две одинаковых полуобмотки с числом витков N₁/2 каждая. Поверх первичной обмотки размещены две вторичные (индуктивные) обмотки: верхняя 4 и нижняя 5 с одинаковым числом витков N₂ каждая, соединенные последовательно встречно.

Вся конструкция помещена в кожух 2 из магнитомягкого материала. Кожух выполняет несущую и защитную функции, но главным его назначением является замыкание магнитного потока якоря ₀ вокруг катушки.

При подаче на первичную обмотку 3 переменного напряжения U, которое будем называть напряжением питания, во вторичных обмотках 4 и 5 наводится соответственно ЭДС Е₁ и ЭДС Е₂. В реальных ДТИП эти ЭДС выпрямляются и сглаживаются. Если геометрический центр якоря 1 находится в геометрическом центре катушки с обмотками 3, 4 и 5, то ЭДС, наведенные в обмотках 4 и 5, одинаковы (Е₁ = Е₂). Их разностный выпрямленный сигнал ΔЕ = Е₁ – Е₂ равен нулю. При перемещении якоря, например вверх на величину , изменяется конфигурация магнитной системы, так что степень взаимной индуктивной связи обмотки 3 с обмоткой 4 увеличится, а с обмоткой 5 уменьшится. При этом разностный сигнал ΔЕ будет положительным (ΔЕ = Е₁ – Е₂ >0).

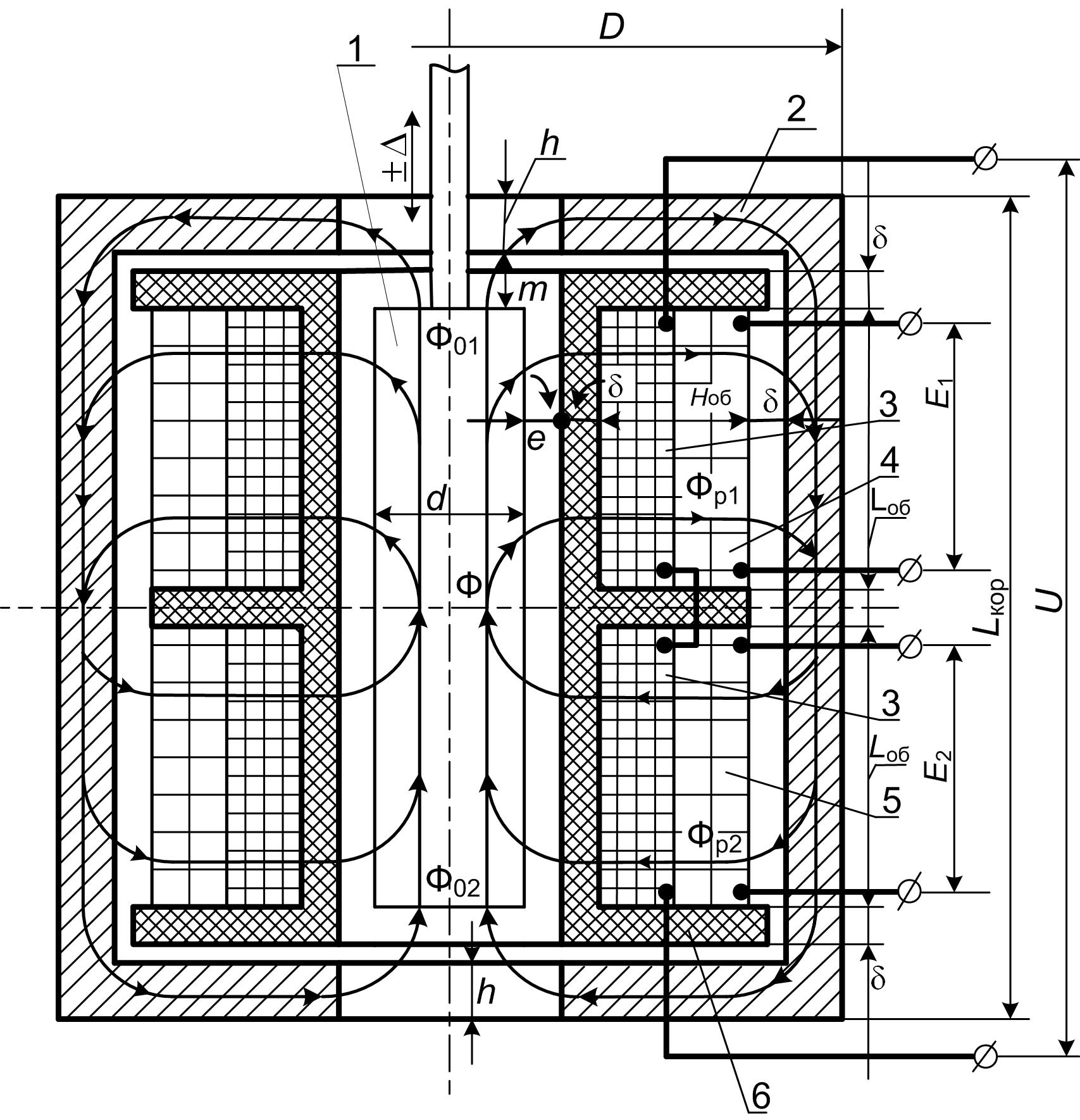
Рис. 2.1. Моделируемый ДТИП:

1 – подвижный якорь из магнитомягкого материала; 2 – кожух из магнитомягкого материала; 3 – две полуобмотки первичной электрической обмотки (обмотка возбуждения); 4 и 5 – две вторичные электрические индуктивные обмотки; 6 – каркас катушки из электроизоляционного материала

С увеличением перемещения  значение сигнала Е будет возрастать. Если якорь переместится вниз от геометрического центра, то степень взаимоиндуктивной связи обмотки 3 с обмоткой 4 уменьшится, а с обмоткой 5 увеличится. При этом разностный сигнал Е станет отрицательным (Е < 0) и с увеличением перемещения  значение сигнала Е будет уменьшаться.

ДТИП предназначен для преобразования линейного перемещения якоря в напряжение. Функция преобразования ДТИП имеет вид

ΔЕ = f(Δ). (2.1)

Она является практически линейной функцией типа

Е = S, (2.2)

где S – чувствительность ДТИП, в относительно небольшой области определения аргумента .

Область определения аргумента функции (2.2) ограничивается неравенством

||  _лин, (2.3)

где _лин – граница линейности функции (2.2).

Выход значений аргумента  за пределы области определения (2.3) приводит к проявлению нелинейности функции (2.1), благодаря краевым эффектам.