4.4. Этапы построения математической модели проектируемого микроамперметра

Построение математической модели микроамперметра необходимо выполнить с учетом трех вариантов электрических схем, характеризующих работу микроамперметра на каждом из трех пределов: «Пр1», «Пр2» и «Пр3».

Этап 1. Моделирование микроамперметра при работе на пределе «Пр1».

Работа микроамперметра на пределе «Пр1» характеризуется электрической схемой рис. 4.2.

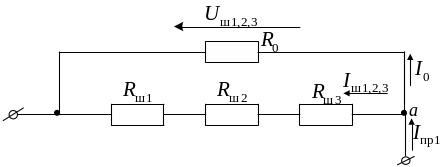
Рис. 4.2. Электрическая схема микроамперметра на пределе «Пр1»

На основании закона Ома для последовательно-параллельной цепи запишем два уравнения:

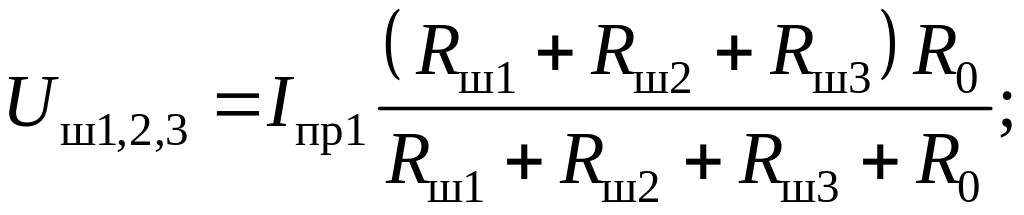(4.1)

(4.2)

Из первого закона Кирхгофа для узла а следует уравнение

. (4.3)

Система уравнений (4.1) – (4.3) дает полное описание электрической схемы на рис. 4.2.

Этап 2. Моделирование микроамперметра при работе на пределе «Пр2».

Работа микроамперметра на пределе «Пр2»характеризуется электрической схемой рис. 4.3.

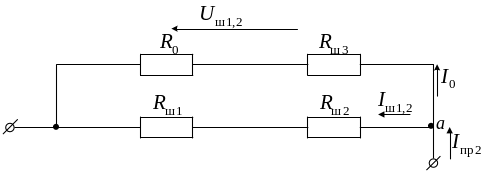
Рис. 4.3. Электрическая схема микроамперметра на пределе «Пр2»

По аналогии с предыдущей электрической схемой составим три уравнения, описывающих электрическую схему рис. 4.3:

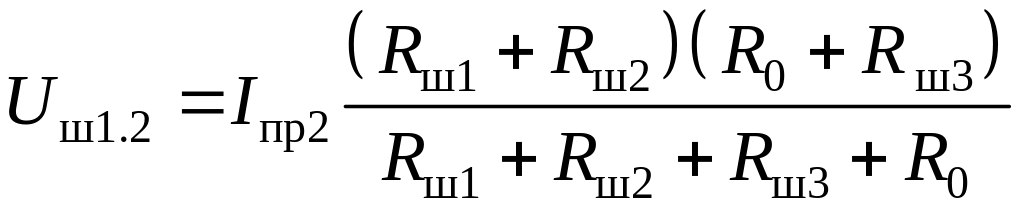; (4.4)

; (4.5)

. (4.6)

Система уравнений (4.4) – (4.6) дает полное описание электрической схемы рис. 4.3.

Этап 3. Моделирование микроамперметра на пределе «Пр3».

Работа микроамперметра на пределе «Пр3» характеризуется электрической схемой рис. 4.4.

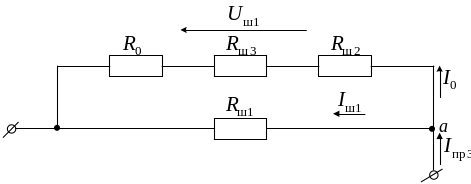
Рис. 4.4. Электрическая схема работы микроамперметра на пределе «Пр3»

По аналогии с предыдущей электрической схемой составим три уравнения, описывающие электрическую схему рис. 4.4:

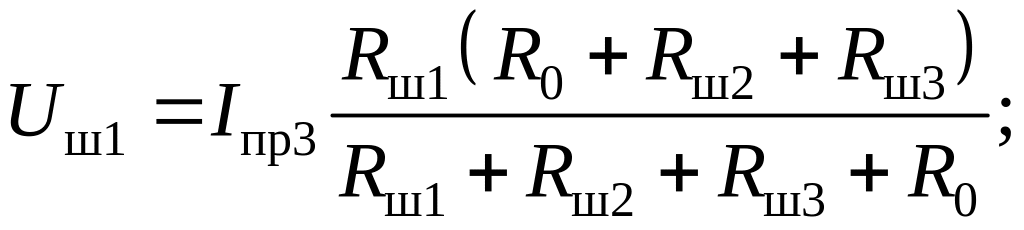(4.7)

(4.8)

(4.9)

Система уравнений (4.7) – (4.9) дает полное описание электрической схемы рис. 4.4.

Этап 4. Определение расчетных значений сопротивлений шунтов R_ш1, R_ш2 и R_ш3.

В результате проведенного анализа нами получена система из девяти линейных уравнений (4.1) – (4.9), описывающая все рабочие состояния микроамперметра. Указанная линейная система содержит девять неизвестных: и может быть решена любым из известных методов. Поскольку все уравнения являются неполными, одним из простых и эффективных методов решения указанной системы может быть метод подстановки.

В результате последовательной подстановки и преобразования получим следующие решения:

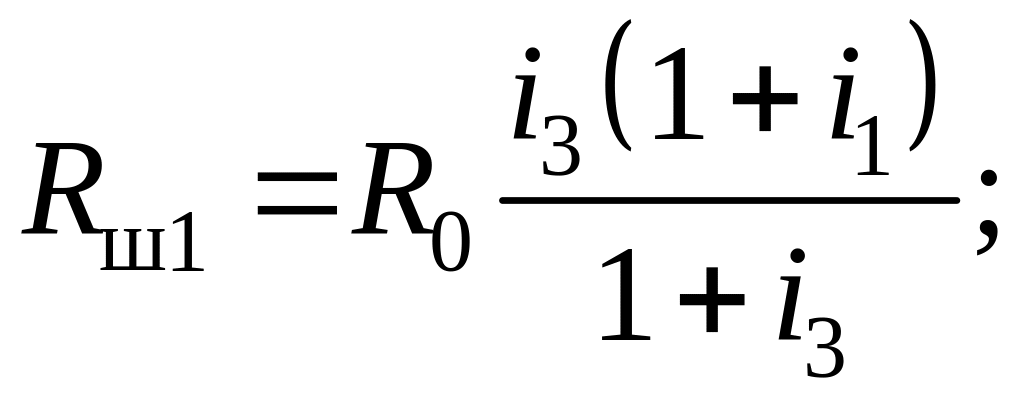(4.10)

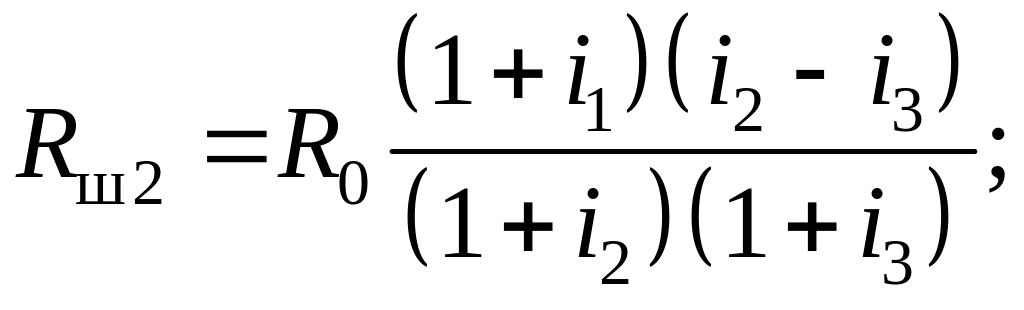(4.11)

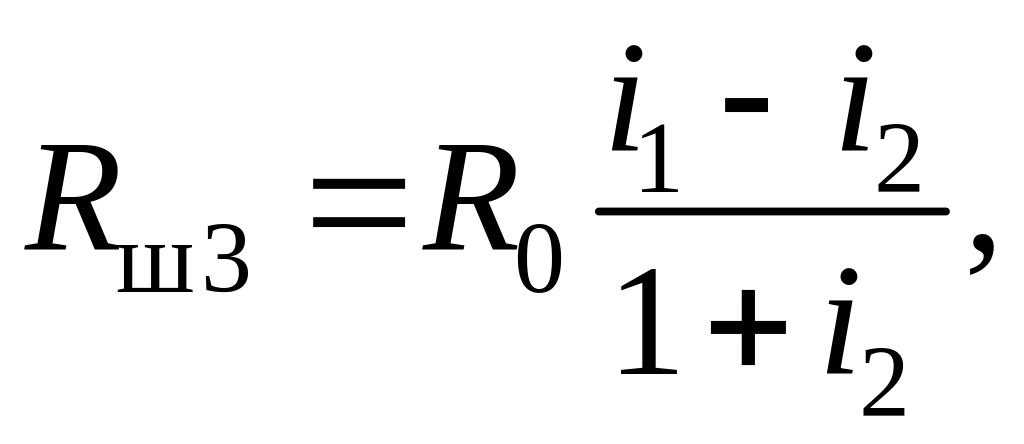(4.12)

где i₁, i₂ и i₃ – расчетные коэффициенты, определяемые соотношениями:

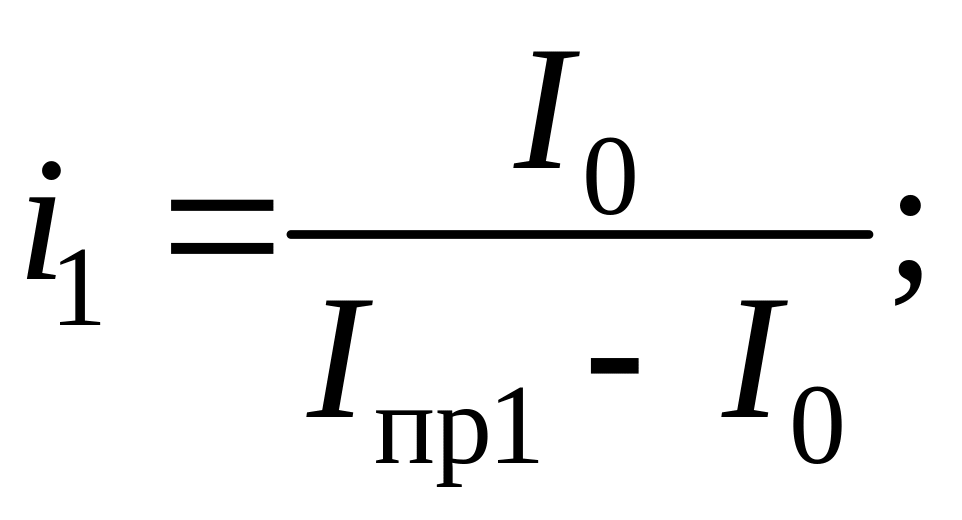(4.13)

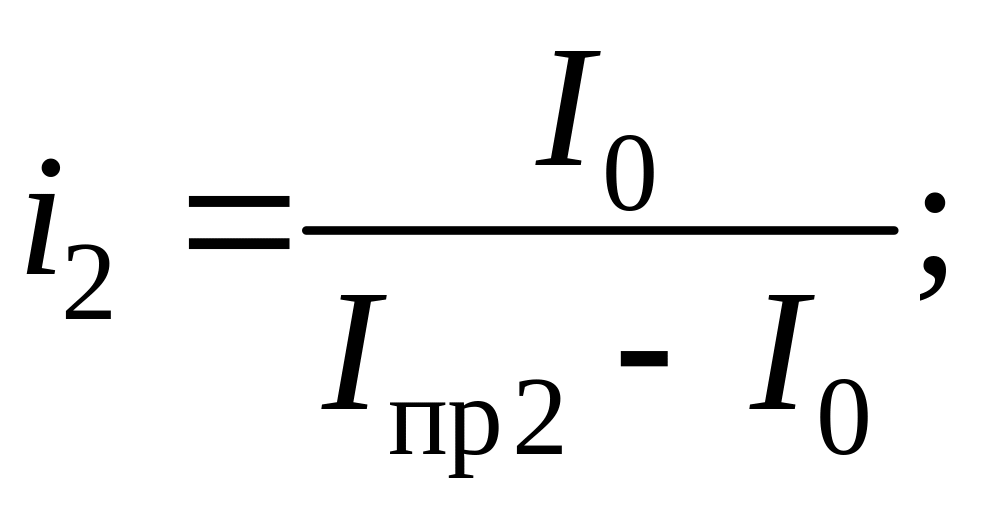(4.14)

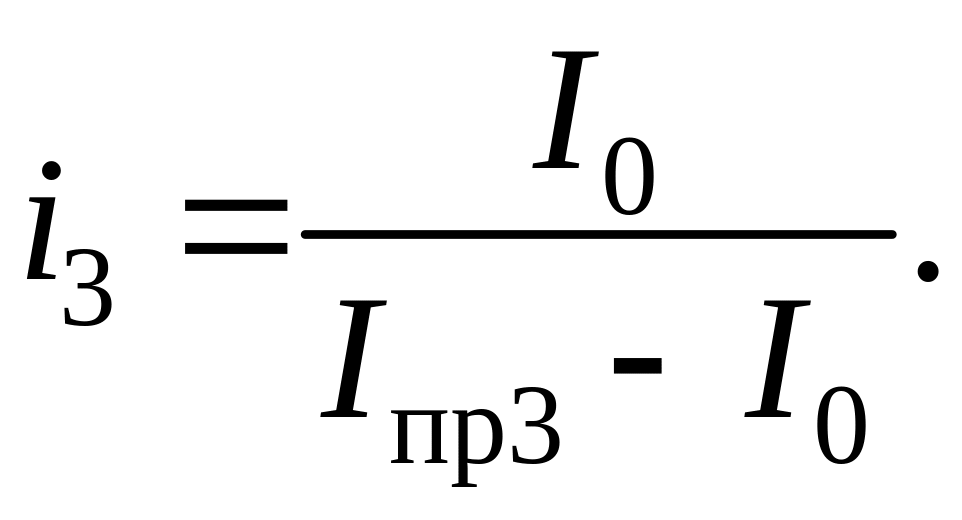(4.15)

4.5. Анализ влияния выбора стандартных значений резисторов на точность результатов измерений тока проектируемым

микроамперметром

4.5.1. Составляющие систематической погрешности

микроамперметра

Основная систематическая погрешность измерения проектируемого микроамперметра складывается из следующих составляющих:

1) основная систематическая погрешность измерения МЭИМ;

2) погрешность измерения, связанная с округлением результатов расчета значений сопротивлений , и ;

3) погрешность измерения, связанная с выбором значений сопротивлений , и , ближайших к их расчетным значениям из ряда предпочтительных значений для резисторов (прил. 4);

4) погрешность измерения, связанная с выбором допустимого отклонения значений резисторов , и от номинального значения этих сопротивлений (прил. 4).

Границы не исключенной основной систематической погрешности проектируемого микроамперметра могут быть рассчитаны как композиция границ отдельных составляющих систематических погрешностей , вызванных перечисленными ранее факторами (Приложение 4). При равномерном распределении не исключенных систематических погрешностей эти границы (без учета знака) вычисляются по формуле

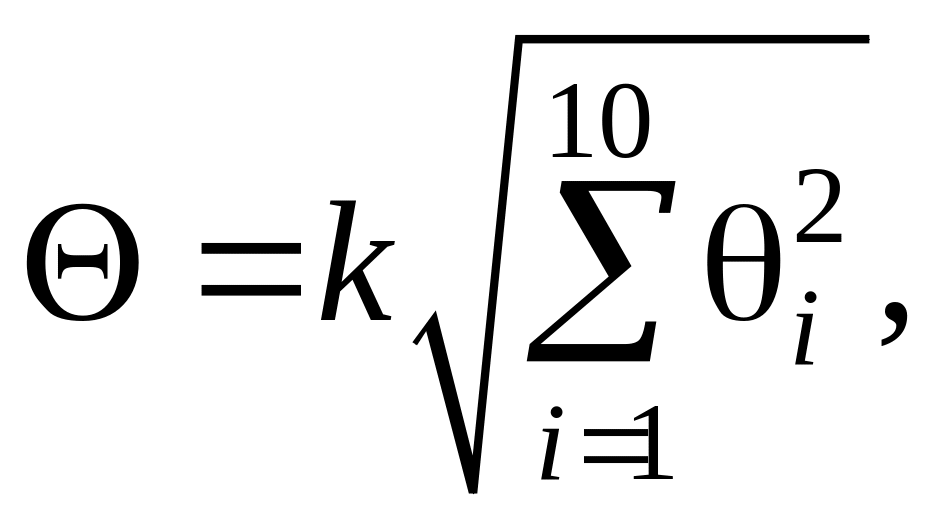(4.16)

где – граница относительной приведенной погрешности измерения МЭИМ; и – границы относительных погрешностей измерения, связанные с округлением результатов расчета значений сопротивлений соответственно , и ; и – границы относительных погрешностей измерения, связанные с выбором значений сопротивлений соответственно , и ближайших к их расчетным значениям из ряда предпочтительных значений для резисторов; и границы относительных погрешностей измерения, связанные с выбором стандартного допустимого отклонения значений сопротивлений резисторов соответственно , и от номинального значения этих сопротивлений; коэффициент, определяемый выбранной доверительной вероятностью , при ; при (прил. 4).

Значение границы погрешности определяется значением класса точности МЭИМ: .

Значения границы погрешности и определяются по формулам:

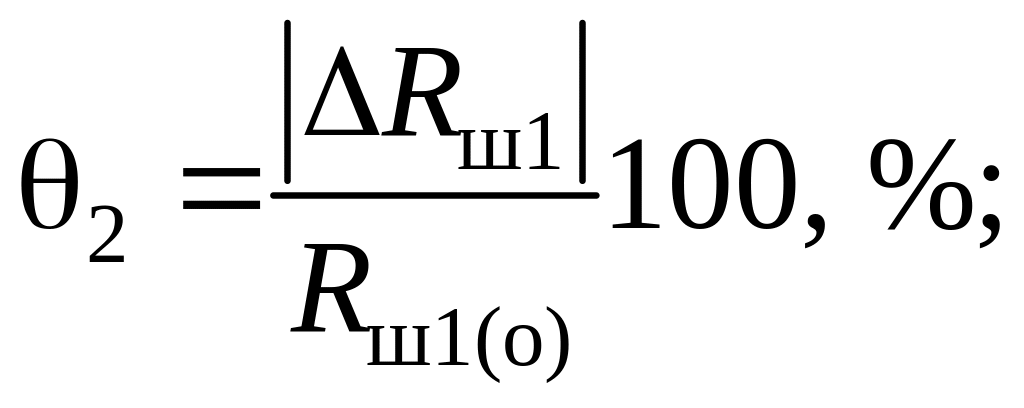(4.17)

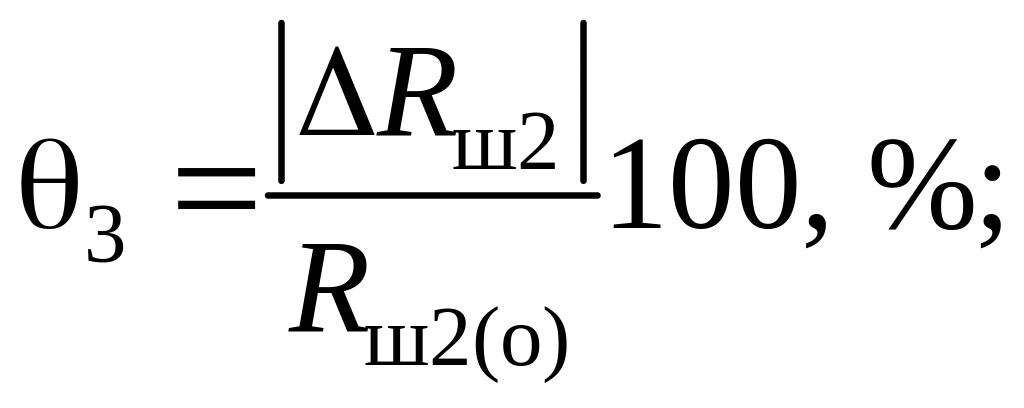(4.18)

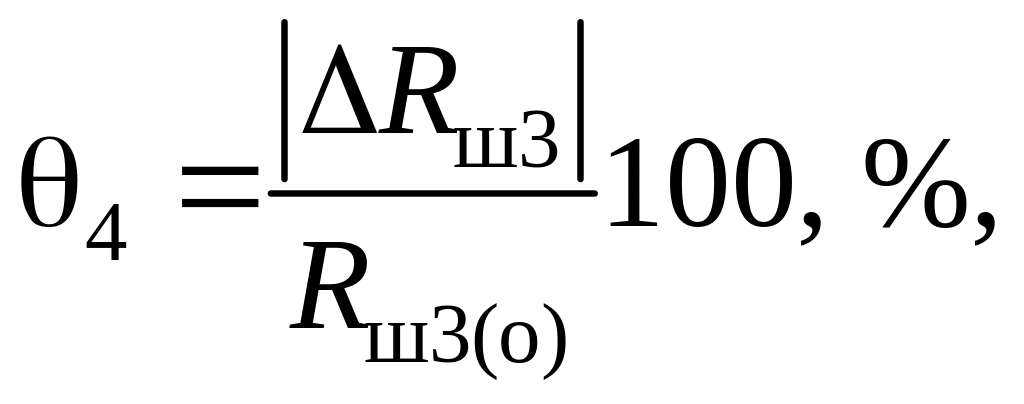(4.19)

где и – округленные значения сопротивлений , и ;

и – отброшенные (добавленные) при округлении части сопротивлений с их знаком ( и ).

Для удобства выбора значений и , ближайших к соответствующим значениям и , необходимо определить возможные диапазоны значений и . В первом приближении эти диапазоны можно оценить из соотношений:

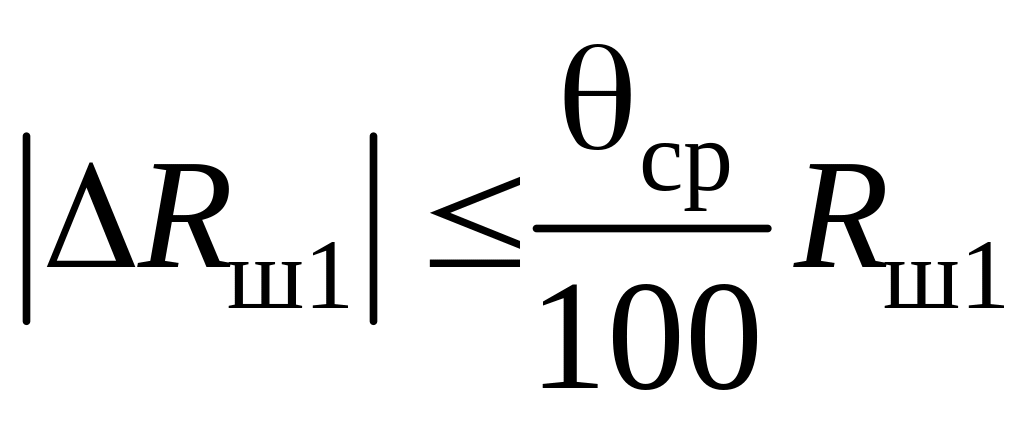; (4.20)

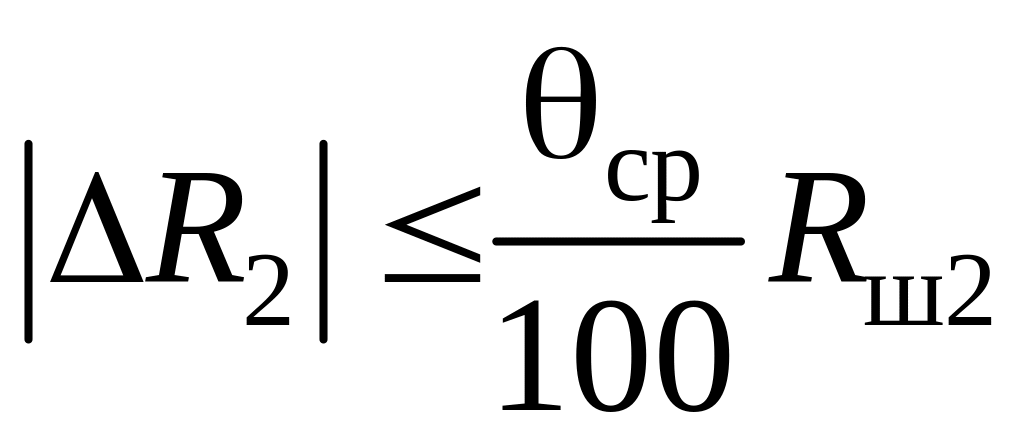; (4.21)

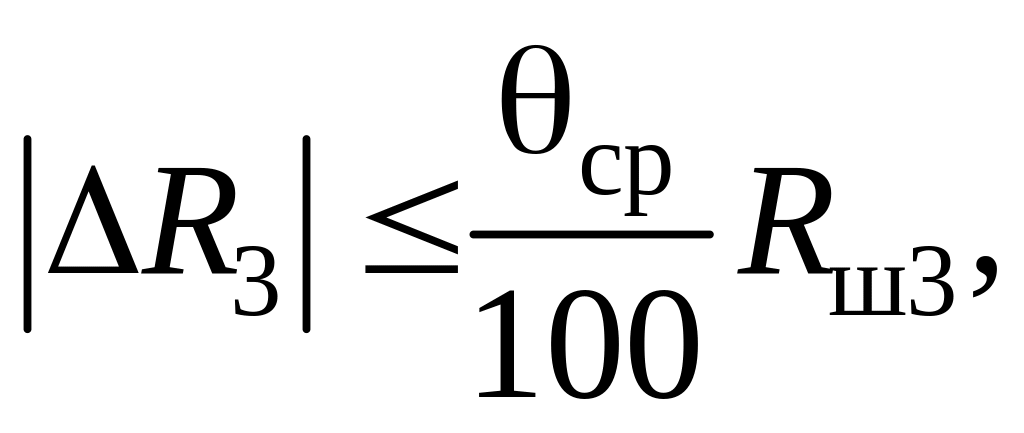(4.22)

где – усредненное значение границ относительных погрешностей ₂, …, ₁₀, определяемое по формуле (4.35).

Соответственно диапазоны изменения значений и можно приближенно оценить из соотношений:

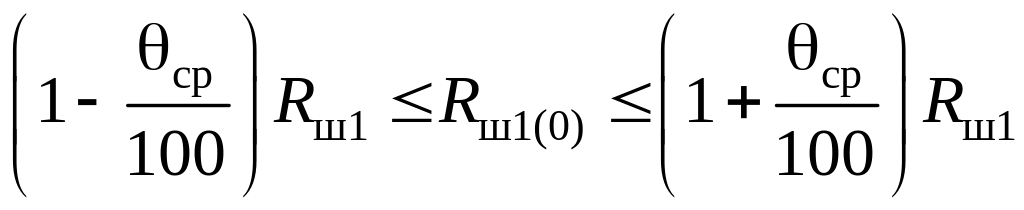; (4.23)

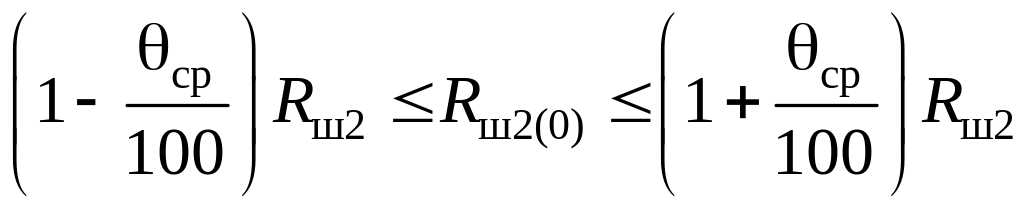; (4.24)

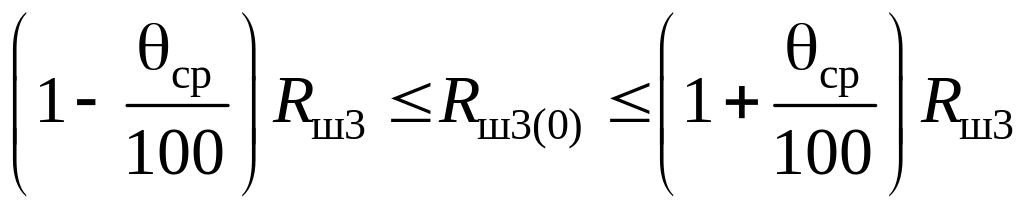. (4.25)

При выборе и из указанных диапазонов за основу берутся условия минимального отличия указанных округленных значений от соответствующих значений и , выбранных из табл. П4.1 или П4.2 (прил. 4, п. 2).

Значения границы погрешности и определяются по формулам:

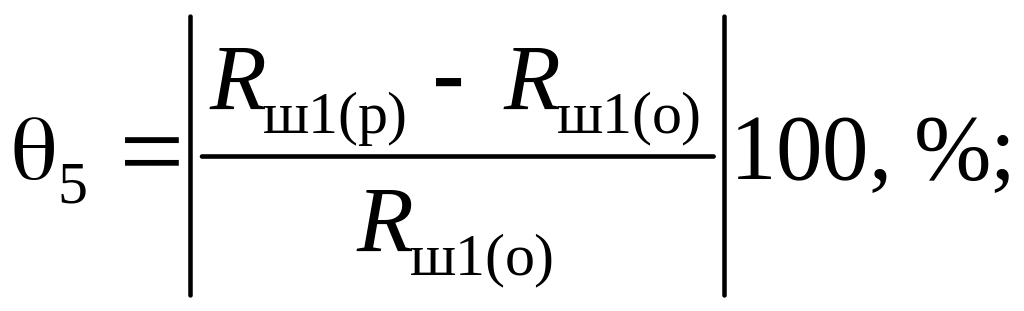(4.26)

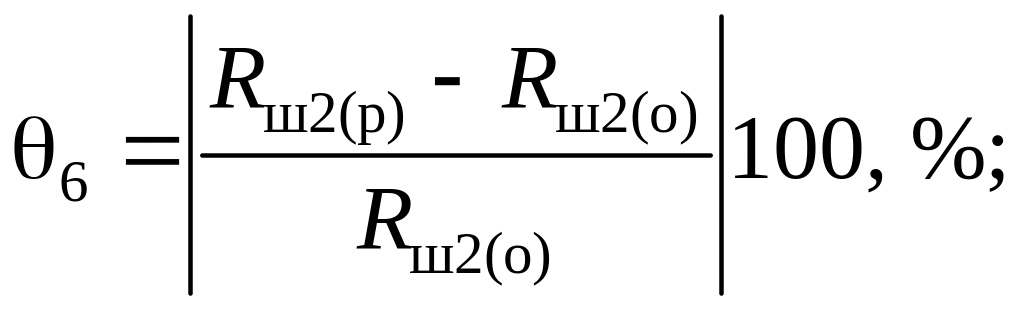(4.27)

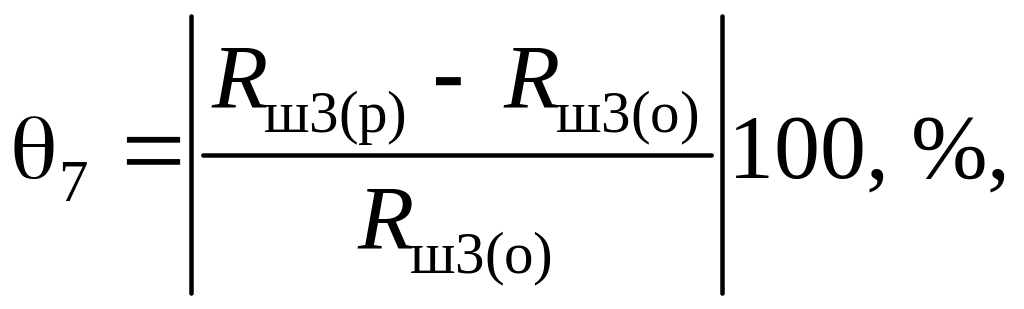(4.28)

где и – значения сопротивлений из ряда предпочтительных значений, ближайшие к соответствующим округленным значениям сопротивлений и .

Значения границ погрешностей и принимаются равными выбранным допустимым отклонениям значений резисторов и от их номинальных значений.