Политропный процесс.

Изотермический и адиабатный процесс являются идеальными. Изотермический процесс может быть реализован бесконечно медленно, адиабатный процесс может происходить в сосуде, стенки которого имеют нулевую теплопроводность, что на практике невозможно.

В природе происходят реальные процессы, являющиеся промежуточными между адиабатными и изотермическими. Такие процессы называются политропными.

При политропном процессе теплоемкость тела или системы постоянна, повышение температуры прямо пропорционально количеству теплоты, сообщенному системе.

.

Согласно первому закону термодинамики

.

После преобразования получим

Проинтегрировав данное выражение, имеем

Обозначим 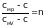, n- показатель политропы.

,

уравнение политропы имеет вид:

Запишем еще две другие формы уравнения политропы

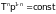. (8)

(9).

Адиабатный и изотермический процессы можно рассматривать как частные случаи политропного процесса.

Для адиабатного процесса С = 0.

Для изотермического процесса ,

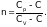
Найдем предел этого отношения, взяв производную от числителя и знаменателя, получим

Для реальных процессов

1 < n < γ.

Реальные газы

При сближении молекул силы взаимодействия начинают играть существенную роль.

В равновесном состоянии внутренняя энергия определяется температурой газа. При переходе газа из одного состояния в другое изменение внутренней энергии зависит только от начального и конечного состояния газа и не зависит от процесса.

Внутренняя энергия – это функция состояния.

.

Уравнение Ван-дер-Ваальса.

Спустя 200 лет после открытия закона Бойля-Мариотта Ван-дер-Ваальса предложил уравнение, которое учитывает силы взаимодействия молекул и объем, который они занимают в сосуде.

. (11)

а – поправка на силы притяжения молекул, b – поправка на объем.

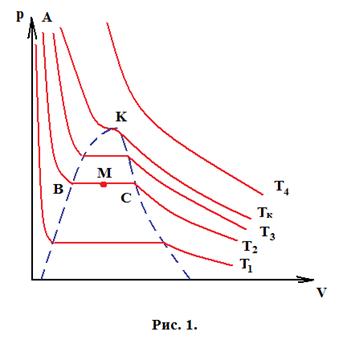
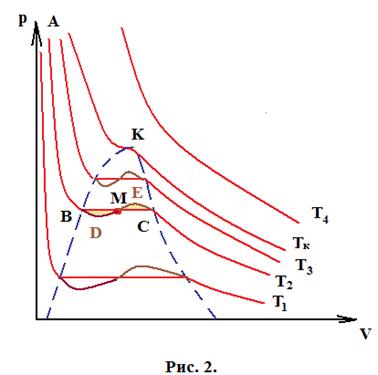
На рис. 1 показаны серии изотерм, построенных на основании эксперимента, а на рис. 2 – кривые Ван-дер-Ваальса.

Рассмотрим изотермический процесс происходящий при температуре Т₂.

Участок кривой Т₂-С (рис. 1) соответствует газообразному состоянию вещества и хорошо совпадает с участком кривой Ван-дер-Ваальса. При уменьшении объема, как мы видим на рис. 1 давление не изменяется, пар становится насыщенным и происходит фазовое превращение пара в жидкость.

На рис. 2 кривая при тех же значениях объема продолжает идти вверх, такие состояния на практике могут быть реализованы, если газ сжимать очень медленно, и в газе нет центров конденсации, которыми являются ионы, частички пыли и т.д.

Состояния, соответствующие участку кривой СЕ являются нестабильными и пар в них будет перенасыщающим. Относительная влажность такого пара может достигать 400%. При попадании в газ иона, вокруг него начинается образование капельки жидкости, если при дальнейшем движении частицы происходит процесс ионизации и последующей конденсации, то по туманному следу можно судить о траектории частицы. На этом эффекте основана камера Вильсона, регистрирующая космические лучи и частицы, получающиеся в результате радиоактивного распада.

Участок С-В на рис. 1 соответствует двухфазному состоянию системы – насыщенный пар и жидкость. Этот участок не описывается уравнением Ван-дер-Ваальса за исключением точки М – точки пересечения кривой отрезком СВ (рис. 2).

При параметрах соответствующих точке В весь пар перешел в жидкость. Дальнейшее уменьшение объема приводит к резкому увеличению давления, так как жидкость слабосжимаема.

Участок кривой ВА соответствует участку кривой ВА на рис. 7.

Состояния, соответствующие DB (рис. 2) также могут быть реализованы, хотя они неустойчивы. Если медленно расширять жидкость, то при отсутствии центров парообразования, система остается в жидком состоянии. Эти состояния соответствуют растянутой жидкости.

Итак уравнение Ван-дер-Ваальса хороша описывает однофазные состояния системы, но не описывает двухфазное состояние – насыщенные пар-жидкость.

Рассмотрим особенности кривых на рис. 1 и 2.

Мы видим, что на рис. 2 при температурах меньших T_к каждому значению давления соответствуют три значения объема, так как уравнение кубическое относительно р.

При температуре равной критической корни вырождаются, и на кривой будет точка перегиба, соответствующая критическому состоянию вещества.

В критическом состоянии исчезает граница между жидкостью и паром, плотность пара становится равной плотности жидкости. Параметры этого состояния называются критическими параметрами – критическое давление р_к и критический объем V_к.

Критические параметры измеряются экспериментально.

Эти параметры можно связать с поправками Ван-дер-Ваальса.

В точке перегиба первая и вторая производные обращаются в нуль.

.

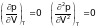Используя эти равенства, из уравнения Ван-дер-Ваальса получим

,

где 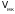- молярный критический объем.