Лекция 2

Основные понятия термодинамики.

В начале 19 века было хорошо изучено превращение кинетической энергии в потенциальную в консервативных системах, то есть был сформулирован закон сохранения механической энергии.

Однако этот закон не распространяется на множество явлений, которые были открыты к этому времени.

В конце 18 века Гальвани обнаружил так называемое животное электричество, в 1820 году Эрстед показал связь электрического тока с магнетизмом. Было открыто, что электрический ток вызывает нагревание проводников, наконец, в 1831 году Фарадей обнаружил явление электромагнитной индукции.

Изучение всего этого многообразия фактов привело ученых к мысли, что существуют переходы одной энергии (субстанции, как это называлось) в другую.

Одним из открывателей закона сохранения энергии был английский пивовар и ученый-любитель Джеймс Джоуль.

Процитируем, как Джоуль понимал закон сохранения энергии.

« Явления природы, механические, химические или в живом организме, состоят исключительно в непрестанном превращении притяжения в пространстве (потенциальной энергии), живой силы (кинетической энергии) и тепла друг в друга. Так поддерживается порядок во Вселенной; ничто не уничтожается, ничто не утрачивается, а весь механизм работает бесперебойно и гармонично. И хотя в ужасном видении Иезекииля, «казалось, будто колесо находилось в колесе», а все чрезвычайно сложно, запутано и вовлечено в тонкости почти бесконечного различия причин, следствий, превращений и устранений, все же совершеннейший порядок сохранялся – все подчинялось непререкаемой воле Божьей».

Энергия может иметь разные формы – механическая энергия, химическая, теплота, энергия электрического и магнитного полей. Каждую из этих энергий мы выражаем через макропараметры.

Внутренняя энергия.

Основными понятиями термодинамики являются внутренняя энергия и энтропия.

Остановимся на первом понятии.

Средняя кинетическая энергия поступательного движения молекул равна .

В газе массой m число молекул равно .

Таким образом, средняя кинетическая энергия поступательного движения молекул газа равна .

Внутренняя энергия системы есть сумма всех видов энергии, имеющихся в изолированной системе.

Напомним, что изолированной системой называется система, не обменивающаяся с внешней средой ни энергией, ни веществом.

Заметим, что закрытыми системами называются системы, обменивающиеся с внешней средой энергией, но не веществом. Соответственно открытые системы обмениваются со средой и энергией, и веществом.

Принимая для рассмотрения процессов в газе модель идеального газа, мы пренебрегли потенциальной энергией взаимодействия молекул. Следовательно, внутренняя энергия идеального газа определяется только кинетической энергией теплового движения молекул.

Если газ одноатомный, то внутренняя энергия равна

.

Если молекулы газа состоят из нескольких атомов, то помимо поступательного движения надо учесть их вращательное движение.

Как это сделать?

Согласно теореме Больцмана о равнораспределении энергии по степеням свободы на каждую степень свободы молекулы приходится энергия, равная .

Число степеней свободы i определяется числом независимых координат, которыми может быть определено положение молекулы (тела) в пространстве.

Мы рассматриваем жесткие молекулы, то есть, считаем, что расстояния между атомами остается постоянным. Фактически мы будем при расчете внутренней энергии пренебрегать энергией колебательного движения атомов, которая в действительности существенно меньше, чем энергия поступательного и вращательного движения.

В случае одноатомного газа число степеней свободы равно i = 3,

двухатомного газа i = 5, если молекулы газа состоят из трех и более молекул i = 6.

Таким образом, средняя энергия молекулы равна .

Следовательно, внутренняя энергия идеального газа определяется выражением:

.

Теплота.

Природа теплоты была не ясна до середины 19 века.

Однако уже Ньютон и Бойль считали, что теплота – это беспорядочное движение частиц.

Большинство же ученых считали, что теплота – это некоторая субстанция, переходящая из одного тела в другое. Эта субстанция называлась теплородом или калориметрической жидкостью и измерялась в калориях.

В результате экспериментов Джоуля было установлено, что теплота может преобразовываться в механическую работу и наоборот. Джоуль также определил, что между механической работой и теплотой существует эквивалент. Некоторое количество механической работы, независимо от способов превращения, всегда производит одно и то же количество теплоты. (4,184 Дж производят 1 кал). Это означало, что теплоту и механическую энергию можно было считать различными проявлениями одной и той же физической величины – энергии.

Энергия, переданная системе в результате теплообмена без совершения работы, называется количеством теплоты.

Количество теплоты, сообщенное системе при ее переходе из одного состояния в другое, зависит от процесса перехода.

Работа.

Работа при постоянном давлении определяется произведением давления на изменение объема газа.

.

Если давление изменяется, то при малом изменении объема .

Тогда при конечном изменении объема

.

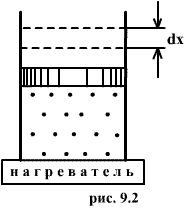
Работа при различных процессах.

При зависимости давления от объема, работа определяется площадью криволинейной трапеции или рассчитывается по формуле.

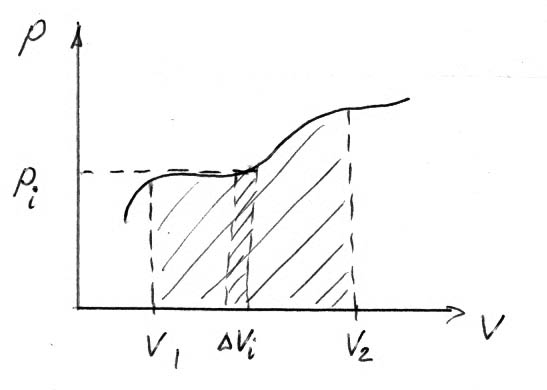
1. При изотермическом процессе работа численно равна площади криволинейной трапеции.

(1)

Из уравнения состояния газа следует .

Подставив это выражение в (1), имеем

.

2. При изобарном процессе работа равна

.

3. При изохорном процессе работа газа равна нулю, так как не происходит изменения объема.

Изменение внутренней энергии системы, как мы говорили, не зависит от процесса, а зависит только от начального и конечного состояний системы.

Изменение внутренней энергии может происходить вследствие двух причин 1) системе сообщается теплота или, наоборот, у системы отбирается некоторое количество теплоты, 2) система совершает механическую работу.

Таким образом, согласно закону сохранения энергии,

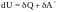. (2)

- работа внешних сил.

Разные обозначения приращения в левой и правой части равенств подчеркивают тот факт, что внутренняя энергия – термодинамический потенциал и, соответственно полный дифференциал, а теплота и работа зависят от процесса.

Первый закон термодинамики можно сформулировать следующим образом: изменение внутренней энергии системы равно сумме количества теплоты, сообщенного системе и работе внешних сил.

При dQ и d > 0 внутренняя энергия системы увеличивается.

Если внешние силы совершают положительную работу, то сила давления газа совершает отрицательную работу:

Тогда первое начало термодинамики запишем

.

Количество теплоты, сообщенное системе, идет на изменение внутренней энергии системы и на работу, совершаемую системой.

Так как изменение внутренней энергии не зависит от процесса, то ее изменение для кругового процесса равно нулю.

.

Учтя (2), имеем

Таким образом, сумма количества теплоты и совершенной работы остается постоянной величиной независимо от пути перехода системы из одного состояния в другое.Как мы говорили dU – полный дифференциал, а величины не являются полными дифференциалами, а функционалами, они зависят от вида функции, описывающей переход из одного состояния в другое.

Теплоемкость.

Теплоемкость тела определяется количеством теплоты, которое необходимо ему сообщить, для повышения температуры на 1 К.

.

О теплоемкости тела или системы имеет смысл говорить, когда тело неоднородное. Например, теплоемкость человека или теплоемкость помещения.

Удельная теплоемкость определяется количеством теплоты, которое надо сообщить 1 кг вещества для повышения температуры на 1 К.

.

Молярная теплоемкость определяется количеством теплоты, которое надо сообщить 1 молю вещества для повышения его температуры на 1 К.

.

Связь молярной и удельной теплоемкостей имеет вид:

.

Первое начало термодинамики для различных процессов.

1. Изотермический процесс.

Для идеальных газов внутренняя энергия зависит только от температуры. Поэтому

dU = 0.

Следовательно, все количество теплоты, поступающее в систему, идет на механическую работу. .

Изотермический процесс является самым выгодным для получения механической работы.

Теплоемкость при изотермическом процессе стремится к бесконечности, так как dT = 0.

2. Изобарный процесс.

При изобарном нагревании или охлаждении газа . При конечном изменении объема работа равна: .

Согласно первому началу термодинамики

.

Из уравнения Менделеева-Клапейрона следует, что при p = const

.

Тогда

.

Молярная теплоемкость идеального газа при постоянном давлении определится выражением:

. (3)

3. При изохорном процессе все тепло, поступающее в систему, идет на изменение внутренней энергии.

.

Молярная теплоемкость газа равна

. (4)

Из (3) и (4), получим связь теплоемкостей при постоянном давлении и при постоянном объеме

.

Это уравнение называется уравнением Майера.

Запишем соотношение теплоемкостей в общем случае.

Найдем изменение внутренней энергии, учтя, что в общем случае для одного моля внутренняя энергия зависит от температуры и объема .

.

Тогда .

Если нагревание происходит при постоянном объеме, то

и .

Если нагревание происходит при постоянном давлении, то

и .

Откуда

.

Для идеального газа внутренняя энергия является функцией температуры и не зависит от объема.

.

.

Для одного моля , откуда .

Мы получаем уравнение Майера

.