2.2. Метод контурных токов.

Метод контурных токов основан на том, что токи всех ветвей могут быть выражены через контурные токи, принятые в качестве независимых переменных и находятся при решении системы независимых уравнений, составленных на основании второго закона Кирхгофа (21). Число независимых уравнений, записанных для контурных токов, равно числу независимых контуров и для цепи, содержащей число узлов q и число ветвей p, количество независимых контуров равно p-q+1. Независимым контуром считается такой контур, у которого по отношению к другим контурам есть хотя бы одна новая ветвь. При составлении системы уравнений по методу контурных токов произвольно задаются положительным направлением контурных токов. Направление обхода обычно принимается совпадающим с направлением контурного тока рассматриваемого контура.

Прежде чем приступить к составлению системы уравнений введем некоторые понятия.

Собственное сопротивление контура – это сумма всех комплексных сопротивлений, входящих в данный контур. Взаимное или общее сопротивление – это комплексное сопротивление, которое является общим для двух или более контуров.

Контурной э.д.с. называется алгебраическая сумма э.д.с. всех идеализированных источников напряжения, входящих в данный контур.

Система уравнений по методу контурных токов в общем виде записывается следующим образом:

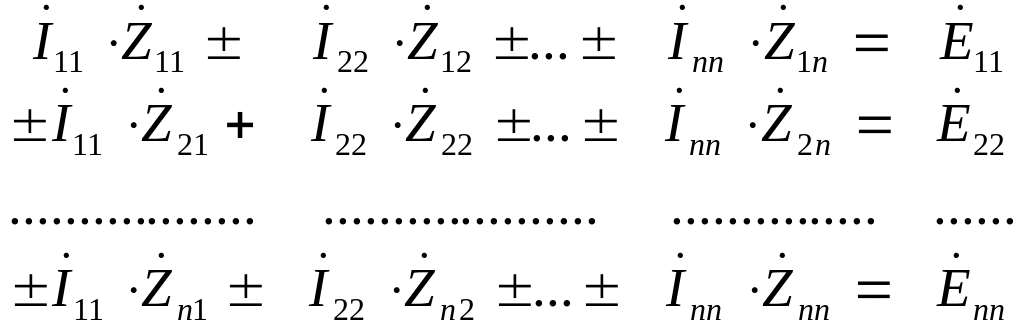
где - собственные комплексные сопротивления контура и всегда входят в уравнения с положительным знаком. – взаимные комплексные сопротивления k и j контуров, причем = . Взаимные сопротивления берутся со знаком плюс при условии совпадения направлений, протекающих по нему контурных токов k и j контуров, в противном случае берется знак минус. – контурные э.д.с., которые представляют из себя алгебраическую Σ э.д.с. действующих в данном контуре, источники э.д.с. входящие в контур берутся со знаком плюс при условии совпадения по направлению с контурным током, а направленные встречно – со знаком минус.

Эту систему уравнений можно записать в матричной форме:

(23)

где - квадратная матрица сопротивлений

=

- матрицы – столбцы контурных токов и контурных э.д.с. Для линейных обратимых цепей, состоящих только из резисторов, емкостей, индуктивностей и независимых источников, матрица контурных сопротивлений не только квадратная, но и в силу равенства взаимного или общего сопротивления k и j контуров, т.е. = , матрица симметрична относительно главной диагонали, имеет порядок n=p-q+1.

В результате решения системы уравнений (22) или (23) получим значение контурных токов.

На основании контурных токов определяются токи в ветвях как сумма контурных токов, если их направление совпадает в ветви и как разность, если их направление противоположно.

Существует много способов решения системы уравнений (22) или (23) и для нахождения контурного тока, выраженного в аналитической форме наиболее удобны формулы Крамера, по которым для k-го контура контурный ток запишется:

(24)

где - определитель системы уравнений (22) или (23), при j = 1,…, n – алгебраическое дополнение (минор со своим или противоположным знаком) элемента определителя системы уравнений (22) или (23).

При машинном анализе электрических цепей, наиболее удобны метод Гаусса и метод LU-разложения, особенно, если число уравнений (независимых контуров) n>4.

Определив контурные токи цепи, переходим к определению токов, протекающих по данной ветви. Применение данного метода для анализа цепей будет рассмотрено более подробно на примере расчета домашнего задания.