Реализация типовых заданий

1. Провести графический анализ остатков

В лабораторной работе № 1 выявили, что на чистый доход (y) предприятий оказывают влияния такие факторы, как использованный капитал (x₂) и численность служащих (x₃).

Для нахождения остатков можно воспользоваться инструментом анализа данных Регрессия. Порядок действий следующий:

а) в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке ОК;

б) заполните диалоговое окно ввода данных и параметров ввода как показано на рисунке 3.1:

Входной интервал Y – диапазон, содержащий данные результативного признака;

Входной интервал Х – диапазон, содержащий данные всех пяти факторов;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

Новый рабочий лист - можно задать произвольное имя нового листа;

Остаток - флажок, указывает вывод остатков и теоретические значения результативного признака.

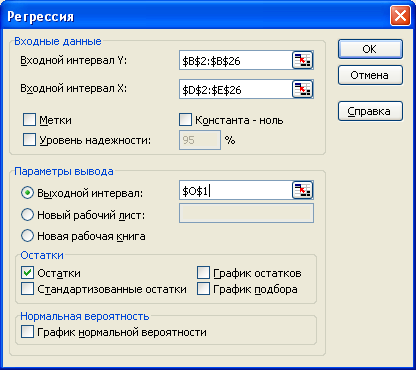
Рисунок 3.1 – Регрессия с остатками

Результаты регрессионного и корреляционного анализа, а также вспомогательные характеристики представлены на рисунке 3.2.

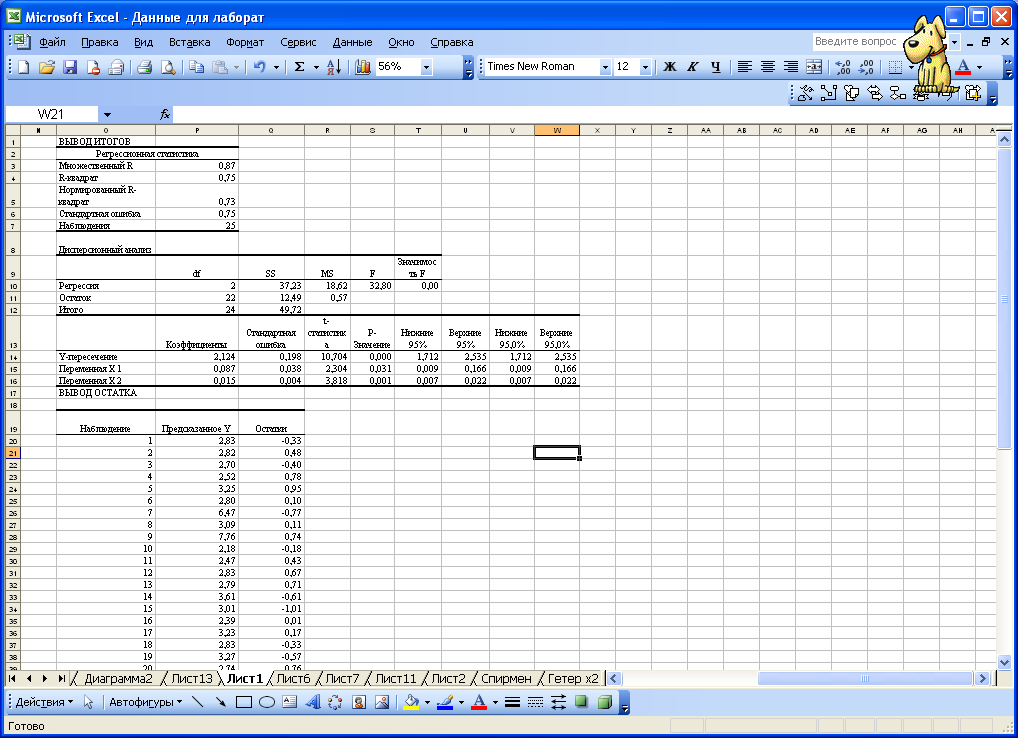
Рисунок 3.2 – Вывод остатков

Проверим остатки полученного уравнения регрессии на гетероскедастичность.

Графический анализ остатков

Построим графики остатков для каждого уравнения (рисунок 3.3 и 3.4)

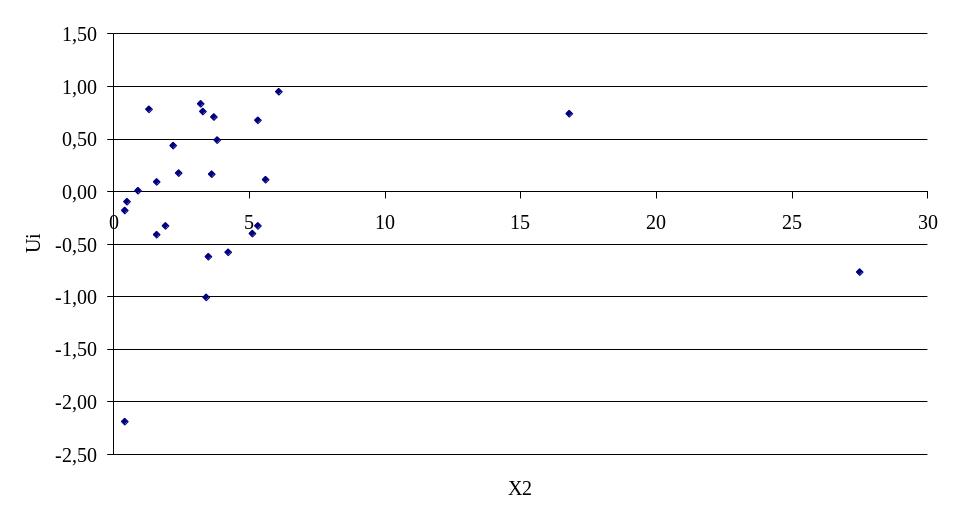
Рисунок 3.3 – График остатков для фактора х₂

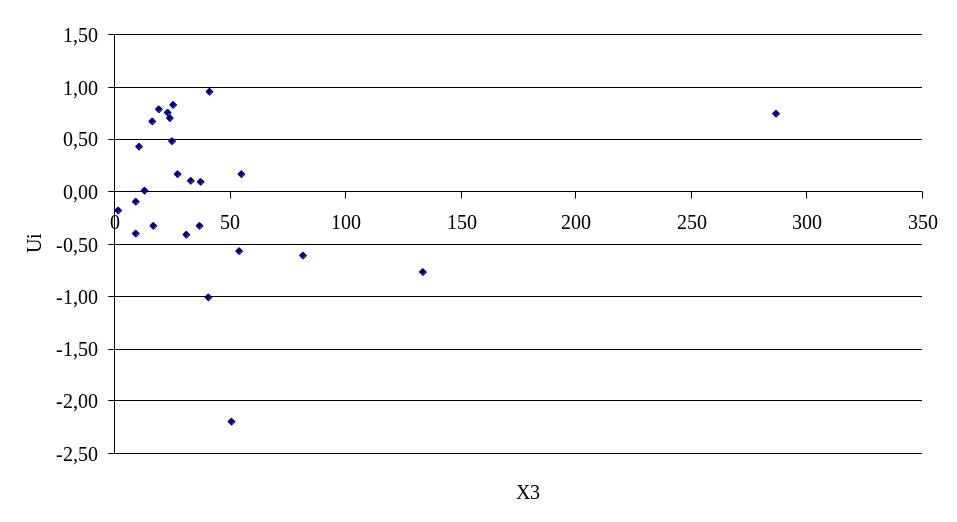
Рисунок 3.4 – График остатков для фактора х₃

Как видно на рисунке отклонения не лежат внутри полуполосы постоянной ширины, это говорит, о зависимости дисперсионных остатков от величины х₃ и о их непостоянстве, т.е. о наличии гетероскедастичности.

Тест Голфелда-Квандта

1. Все n наблюдений упорядочиваются по величине X₂ и X₃.

Таблица 3.1 – Упорядоченные значения по фактору х₂

№п/п
1	2	0,4
2	0,7	0,4
3	2,2	0,5
4	2,4	0,9
5	3,3	1,3
6	2,9	1,6
7	2,3	1,6
8	2,5	1,9
9	2,9	2,2
10	2,9	2,4
11	3,6	3,2
12	3,5	3,3
13	2	3,4
14	3	3,5
15	3,4	3,6
16	3,5	3,7
17	3,3	3,8
18	2,7	4,2
19	2,3	5,1
20	3,5	5,3
21	2,5	5,3
22	3,2	5,6
23	4,2	6,1
24	8,5	16,8
25	5,7	27,5

Таблица 3.2 – Упорядоченные значения по фактору х₃

№п/п
1	1,6	2
2	8,9	2,2
3	9,2	2,3
4	10,3	2,9
5	12,9	2,4
6	16,4	3,5
7	16,5	2,5
8	19,3	3,3
9	22,8	3,5
10	23,8	3,5
11	24,9	3,3
12	25,2	3,6
13	27,2	2,9
14	31,1	2,3
15	32,9	3,2
16	36,9	2,5
17	37,2	2,9
18	40,4	2
19	40,8	4,2
20	50,4	0,7
21	53,8	2,7
22	54,6	3,4
23	81,5	3
24	133,5	5,7
25	286,5	8,5

2. Исключим С центральных наблюдений, разобьем совокупность на две части: а) со значениями x ниже центральных; б) со значениями x выше центральных.

Пусть С=5, это наблюдения с порядковыми номерами 11-15.

3. Оцениваются отдельные регрессии для первой подвыборки (10 первых наблюдений) и для третьей подвыборки (10 последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии по первой подвыборке (сумма квадратов отклонений 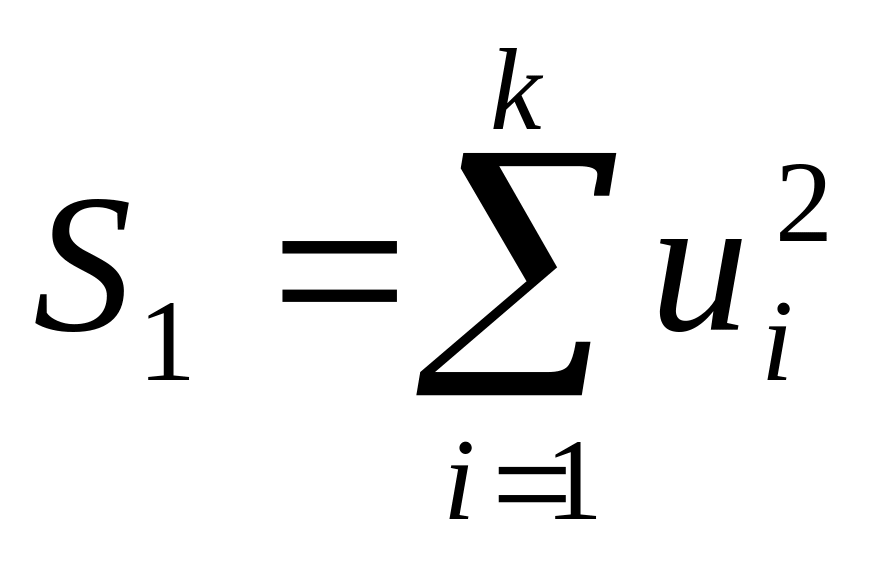) будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений ).

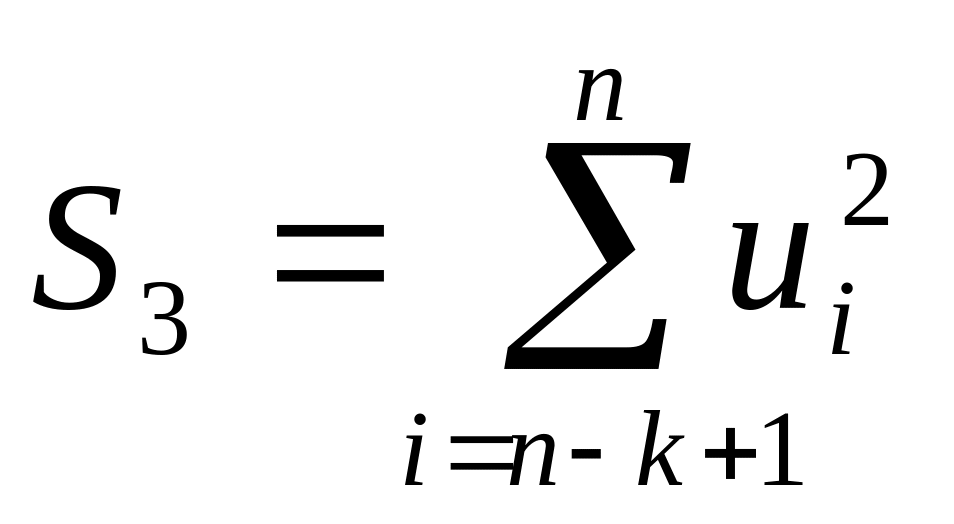4. По каждой части находим уравнение регрессии (рисунок 3.5)

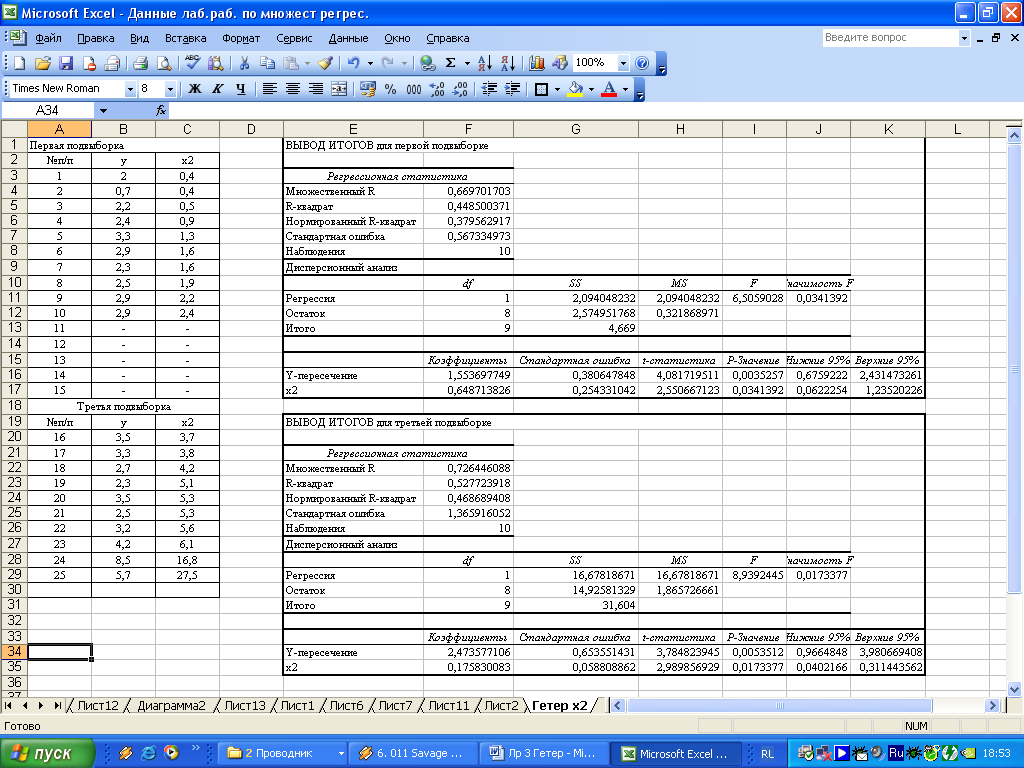
Рисунок 3.5 – Вывод итогов для подвыборок для фактора х₂

5) Для сравнения соответствующих дисперсий строится следующая F-статистика:

При сделанных предположениях относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы v₁=v₂=(n-C-2m)/2.

6) Если , то гипотеза об отсутствии гетероскедастичности отклоняется ( - выбранный уровень значимости).

По проведенным расчетам мы получили, что следовательно в ряду остатков обнаружена гетероскедастичность.

Аналогично проводится анализ для фактора х₃.