
- •Содержание
- •Введение
- •1 Требования к выполнению лабораторных работ
- •Реализация типовых заданий
- •Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов по данным о деятельности крупнейших компаний сша в 2007 г.
- •2 Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.
- •3 Оцените с помощью f-критерия Фишера-Снедекора значимость уравнения линейной регрессии и показателя тесноты связи.
- •Оцените статистическую значимость коэффициентов регрессии с помощью t- критерия Стьюдента.
- •5. Оцените качество уравнения через среднюю ошибку аппроксимации.
- •Рассчитайте матрицу парных коэффициентов корреляции и отберите информативные факторы в модели. Укажите коллинеарные факторы.
- •7. Постройте модель в естественной форме только с информативными факторами и оцените ее параметры.
- •8. Постройте модель в стандартизованном масштабе и проинтерпретируйте ее параметры.
- •9. Рассчитайте прогнозное значение результата, если прогнозное значение факторов составляют 80% от их максимальных значений.
- •10. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости .
- •11. По полученным результатам сделайте экономический вывод.
- •Реализация типовых заданий
- •Реализация типовых заданий
- •Провести графический анализ остатков
- •Графический анализ остатков
- •Тест Голфелда-Квандта
- •Тест ранговой корреляции Спирмена
- •Метод рядов
- •Критерий Дарбина – Уотсона
- •Реализация типовых заданий Степенная модель регрессии
- •Показательная модель регрессии
- •Гиперболическая модель регрессии
- •Прогнозирование по тренд – сезонной аддитивной модели
- •Прогнозирование по тренд – сезонной мультипликативной модели
- •Прогнозирование по модели регрессии с включением фактора времени и фиктивных переменных
- •Построение модели ar (p) в statistica
- •Реализация типовых заданий
- •Список использованных источников
- •Приложение а
- •Исходные данные для выполнения лабораторных работ
7. Постройте модель в естественной форме только с информативными факторами и оцените ее параметры.
Построим уравнение множественной линейной регрессии следующего вида:
![]() .
.
Параметры вычисляем аналогично пункту 1 (рисунок 1.7).
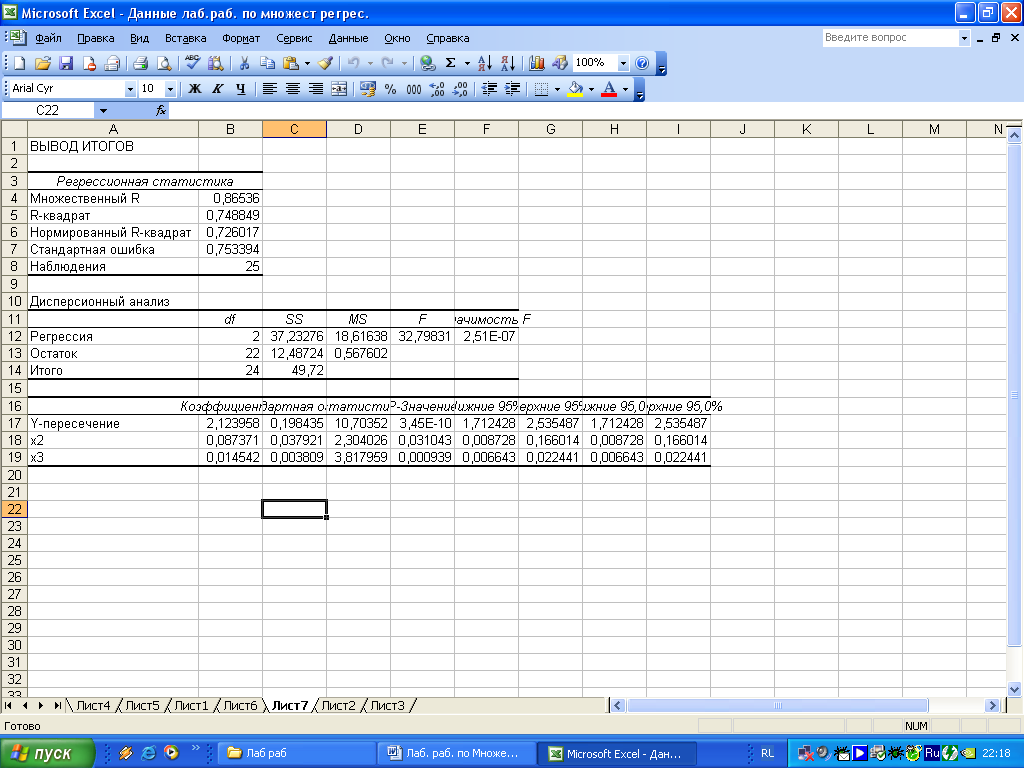
Рисунок 1.7 – Результат применения инструмента «Регрессия»
Получаем
уравнение следующего вида:
![]() .
.
Уравнение в целом, а также его параметры являются статистически значимыми.
8. Постройте модель в стандартизованном масштабе и проинтерпретируйте ее параметры.
Уравнение
в стандартизованном масштабе имеет
вид:
![]() .
.
Расчет β – коэффициентов выполним по формулам
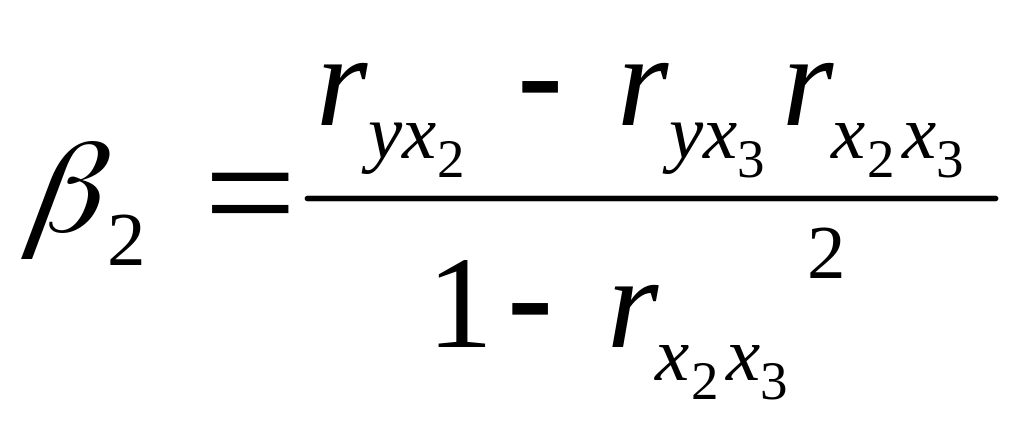 ;
;
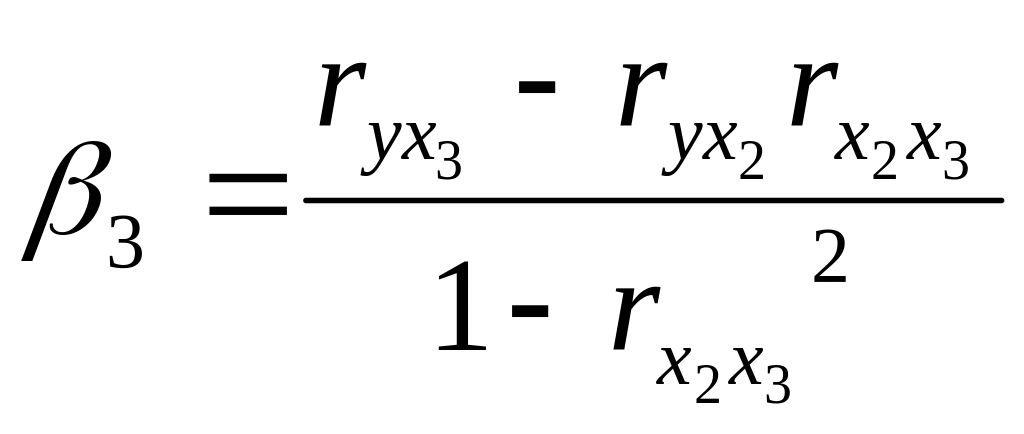 .
.
Парные коэффициенты корреляции берутся из матрицы (рисунок 1.6):
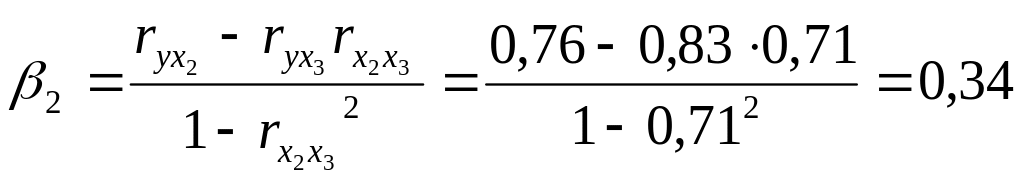
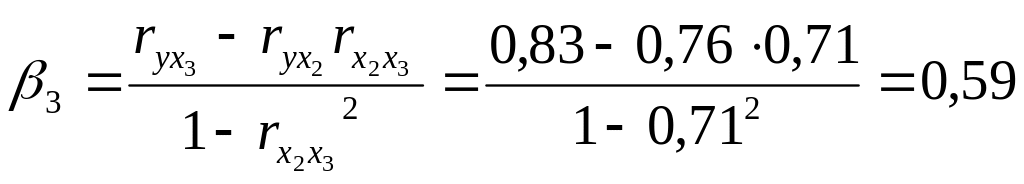
Получим
уравнение
![]() .
.
Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результативный признак, если соответствующий фактор изменится на 1 сигму при неизменном среднем уровне других факторов.
В
нашем случае, при увеличении использования
капитала на 1 сигму чистый доход увеличится
на 0,34 сигм, при условии, что численность
служащих остаются на прежнем уровне.
Аналогично вывод для
![]() .
.
9. Рассчитайте прогнозное значение результата, если прогнозное значение факторов составляют 80% от их максимальных значений.
Рассчитаем ожидаемое прогнозное значение чистого дохода как точечный прогноз путем подстановки в уравнение регрессии прогнозные значения факторов:
найдем максимальное значение для фактора (рисунок 4):
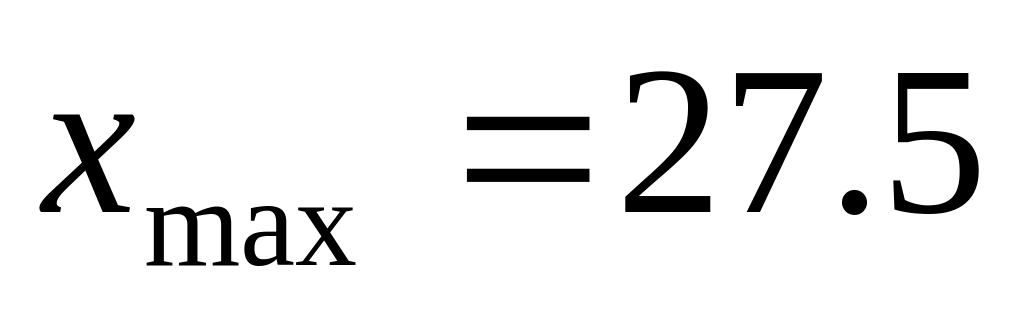
найдем максимальное значение для фактора (рисунок 4):
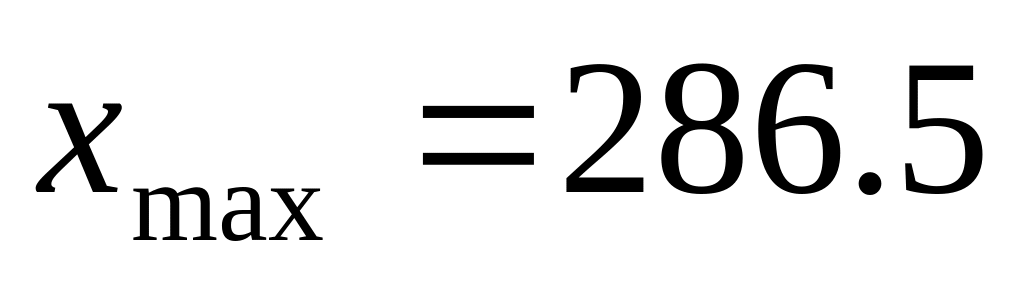
найдем прогнозные значения факторов:
для
фактора
:
![]()
для
фактора
:
![]()
подставим прогнозные значения факторов в уравнение
![]() .
.
В результате получим:
![]()
Таким образом, при прогнозных значениях использованного капитала 22 млдр. долл. и численности служащих 229,2 тыс. чел. чистый доход крупнейших компаний США составит 7,47 млрд. долл.
10. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости .
Доверительный интервал прогноза имеет следующий вид:
![]()
где
![]() - средняя ошибка прогнозируемого значения
- средняя ошибка прогнозируемого значения
![]() ;
;
![]() - вектор-столбец
прогнозных значений факторов;
- вектор-столбец
прогнозных значений факторов;
![]() - стандартная
ошибка
- стандартная
ошибка
![]() .
.
Рассчитаем доверительный интервал прогноза по следующим этапам:
составим вектор-столбец
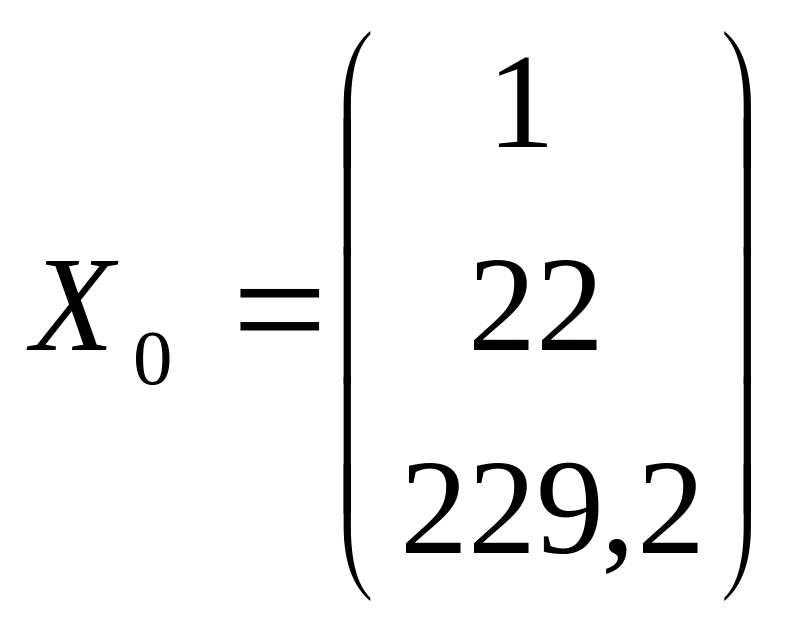
найдем транспонируемый вектор-столбец
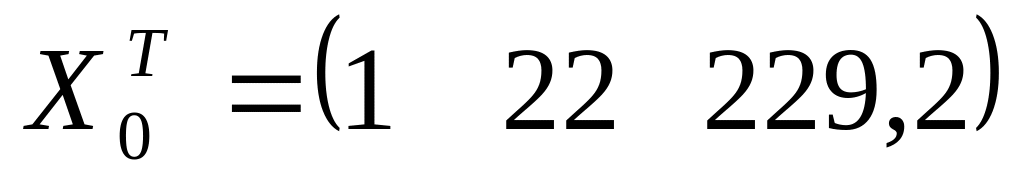
из рисунка 4
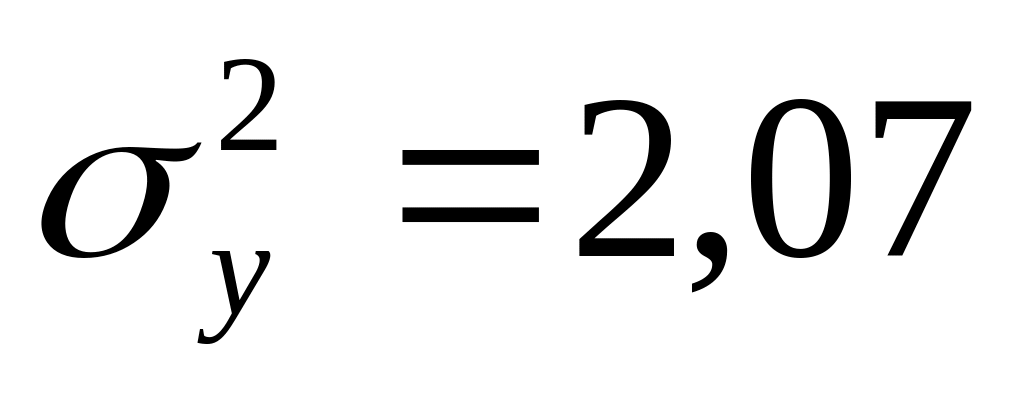
найдем стандартную ошибку
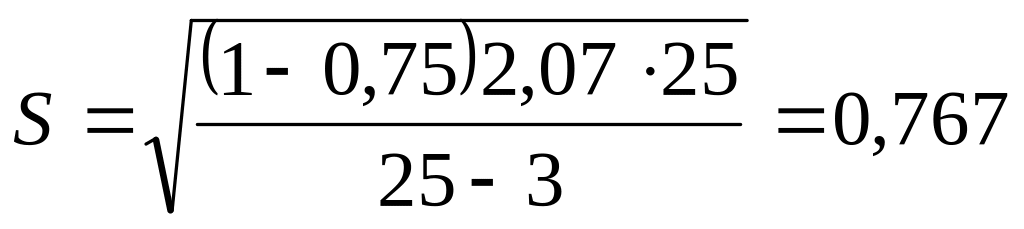
составим матрицу X - 25 наблюдаемых значений независимых переменных и , размер которой 25
 3
(добавлен единичный столбец для
определения a0)
3
(добавлен единичный столбец для
определения a0)найдем произведение
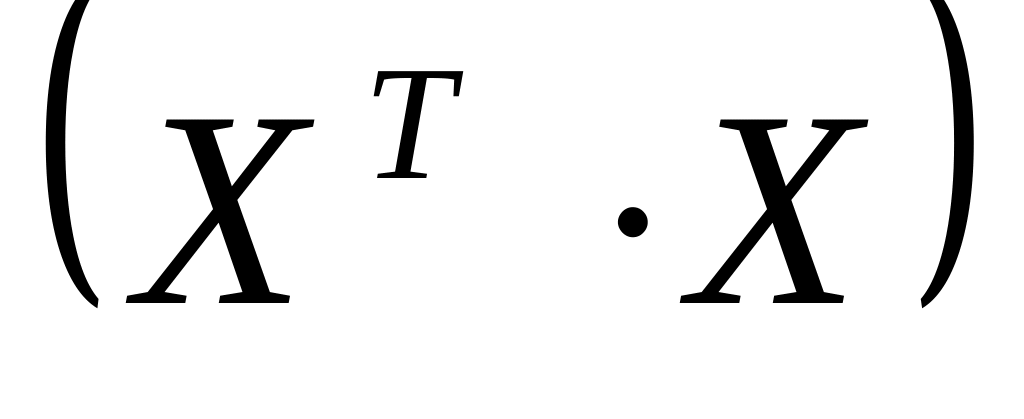
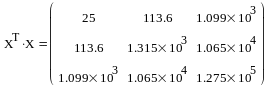
найдем
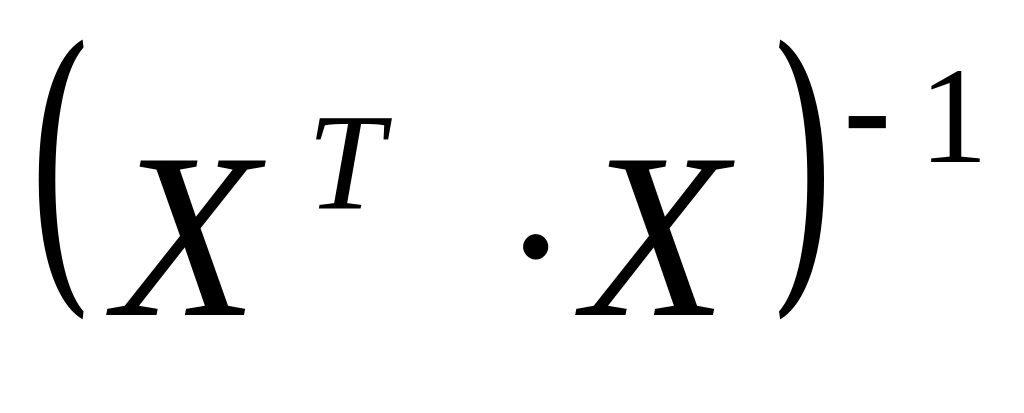
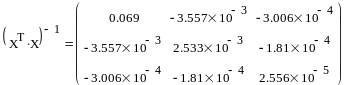
найдем выражение
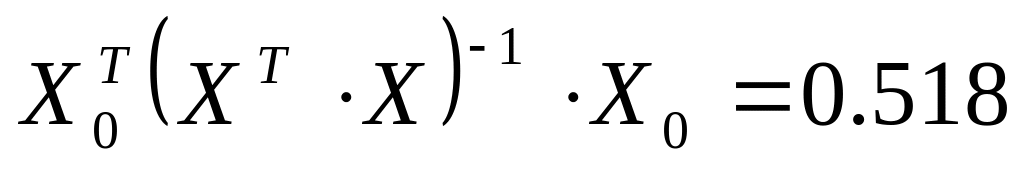
вычислим среднюю ошибку прогнозируемого значения
![]()
по таблицам распределения Стьюдента находим табличное значение
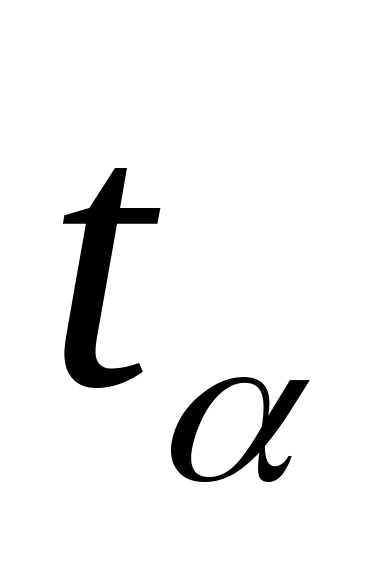 при уровне
значимости 0,05 и числе степеней свободы
22.
при уровне
значимости 0,05 и числе степеней свободы
22.
![]()
составляем доверительный интервал:
![]()
Значит, с вероятность 95 % можно сказать, что чистый доход будет колебаться от 6,33 до 8,61 млрд. долл. при использованном капитале в 22 млрд. долл. и численности служащих 229,2 тыс. чел.
