2 Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.

Средние коэффициенты эластичности показывают, на сколько процентов от значения своей средней изменяется результат при изменении фактора на 1 % от своей средней и при фиксированном воздействии на y всех прочих факторов, включенных в уравнение регрессии. Для линейной зависимости

,

где - коэффициент регрессии при в уравнении множественной регрессии.

Средние значения признаков могут быть получены с помощью инструмента анализа данных Описательная статистика. Для этого выполните следующие шаги:

1. введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2. в главном меню выберите последовательно пункты Сервис / Анализ данных / Описательная статистика, после чего щелкните по кнопке ОК;

3. заполните диалоговое окно ввода данных и параметров вывода (рисунке 1.3).

Рисунок 1.3 – Диалоговое окно ввода параметров инструмента «Описательная статистика»

Результаты вычисления соответствующих показателей для каждого признака представлены на рисунке 1.4.

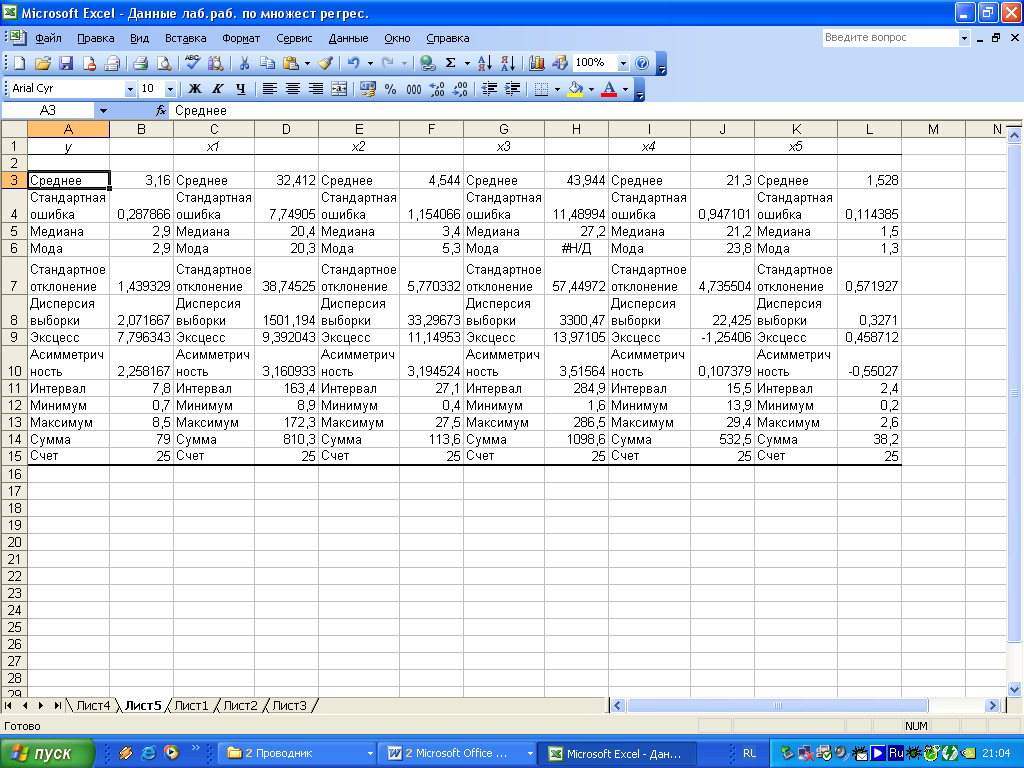
Рисунок 1.4 – Результат применения инструмента «Описательная статистика»

Здесь ,

,

,

,

.

По значениям средних коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат y признаков факторов и , чем признаков факторов , и .

Средний коэффициент эластичности , показывает, что с увеличением оборотного капитала на 1 %, чистый доход увеличивается в среднем на 0,04 %, при условии, что другие факторы остаются постоянными. Аналогично делаются выводы по другим коэффициентам.

3 Оцените с помощью f-критерия Фишера-Снедекора значимость уравнения линейной регрессии и показателя тесноты связи.

Оценку надежности уравнения регрессии в целом и показателя тесноты связи дает F-критерий Фишера:

.

Для проверки значимости уравнения выдвигаем две гипотезы:

Н₀: уравнение регрессии статистически не значимо;

Н₁: уравнение регрессии статистически значимо.

По данным таблиц дисперсионного анализа, представленным на рисунке 1.2, =12,56. Вероятность случайно получить такое значение F-критерия составляет 0,0000, что не превышает допустимый уровень значимости 5 %; об этом свидетельствует величина P – значение из этой же таблицы. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи .

4. Оцените статистическую значимость коэффициентов регрессии с помощью t- критерия Стьюдента.

Выдвигаем две гипотезы:

Н₀: коэффициенты регрессии статистически не значим, т.е. равны о;

Н₁: коэффициенты регрессии статистически значимы, т.е. отличны от нуля.

Значения случайных ошибок параметров с учетом округления равны (рисунок 1.2):

Они показывают, какое значение данной характеристики сформировались под влиянием случайных факторов. Эти значения используются для расчета t-критерия Стьюдента (рисунок 2):

.

Если значения t-критерия больше 2,09, можно сделать вывод о существенности параметра, который формируется под воздействием неслучайных причин. Здесь все параметры являются статистически не значимыми.

На это же указывает показатель вероятности случайных значений параметров регрессии: если α меньше принятого нами уровня (обычно 0,1; 0,05 или 0,01), делают вывод о неслучайной природе данного значения параметра, т.е. о том, что он статистически значим и надежен. В противном случае принимается гипотеза о случайной природе значения коэффициентов уравнения.