5 Лабораторная работа 1 Вероятностная оценка существенности параметров тренда и колеблемости

Цель занятия: научиться оценивать существенность параметров линейного, параболического и экспоненциального трендов, а также также давать сравнительную оценку колеблемости временных рядов.

Контрольные вопросы

1 Какой критерий используется для вероятностной оценки параметров трендов?

2 Какой критерий используется для вероятностной оценки коэффициента колеблемости?

3 Как рассчитываются доверительные границы тренда?

4 Как рассчитываются доверительные границы коэффициента колеблемости?

5 Какой критерий используется для сравнения интенсивности колебаний во временных рядах?

Задания

По данным практического занятия 4:

1 Найдите доверительные границы для показателя колеблемости в генеральной совокупности.

2 Сравните колеблемость в первой половине анализируемого ряда с колеблемостью во второй его половине.

3 На основе полученных данных сделайте выводы о сходстве или различии колеблемости во временном ряду.

Реализация типовых задач

Оценим надежность параметра b линейного тренда. Для этого рассчитывается t-критерий Стьюдента по формуле (необходимые расчеты представлены в Приложении А): ,

где

Соответственно расчетное значение t-критерия равно: . Табличное значение критерия для 22 степеней свободы на уровне значимости 0,05 составляет 2,07. Следовательно, с вероятностью 95 %, параметр b линейного тренда отличен от нуля.

Для основного параметра параболы второго порядка c средняя ошибка репрезентативности вычисляется по формуле:

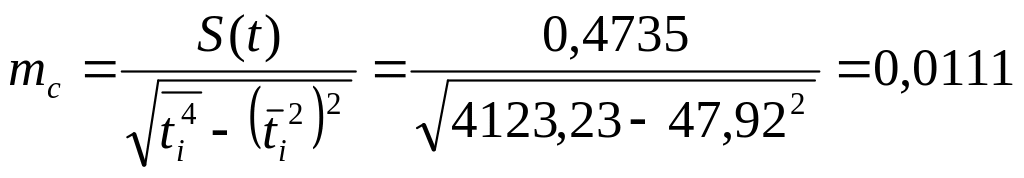
Критерий Стьюдента равен: . Табличное значение при 21 степени свободы составляет 2,08. Таким образом, гипотеза о равенстве нулю коэффициента не может быть отвергнута, с вероятностью 95 %.

Формула средней ошибки логарифма коэффициента изменения k имеет вид:

Критерий Стьюдента: . Табличный критерий при 22 степенях свободы и значимости 0,05 равен 2,07. Полученное значение критерия много больше табличного, следовательно, вероятность нулевой гипотезы можно считать равной нулю.

Таким образом, вероятностная оценка параметров трендов показала надежность параметров линейного и экспоненциального трендов. Оценим колеблемость урожайности зерновых культур относительно линейного тренда, руководствуясь правилом отбора наиболее простых моделей.

Найдем доверительные границы для коэффициента колеблемости в генеральной совокупности.

Среднюю ошибку репрезентативности выборочной оценки генерального коэффициента колеблемости определим по формуле:

.

С вероятностью 0,95 при 22 степенях свободы доверительные границы генерального коэффициента колеблемости составят или от 4,24 % до 7,9 %.

Сравним колеблемость урожайности зерновых культур в 1983-1994 г.г. с колеблемостью в 1995-2006 г.г. Для этого применим Критерий Бартлетта «М».

При сравнении двух дисперсий и равном числе уровней средние арифметическая и геометрическая будут не взвешенные и формулы для их расчета примут вид:

, ,

где и - дисперсии соответственно для первого и второго периодов.

Для расчета дисперсий по подпериодам построим вспомогательную таблицу 5.1.

Таблица 5.1- Расчет дисперсии

Годы		Годы
1	2	3	4
1983	0,32	1995	0,17
1984	0,01	1996	0,02
1985	0,01	1997	0,00
1986	0,07	1998	0,00
1987	0,12	1999	0,10
1988	0,53	2000	1,19
1989	0,04	2001	1,14
1990	0,17	2002	0,42
1991	0,11	2003	0,14
1992	0,02	2004	0,08
1993	0,00	2005	0,26
1994	0,26	2006	0,86
итого	1,67	Итого	4,39
	0,14		0,36

Тогда

,

.

Критерий Бартлетта «М» равен:

,

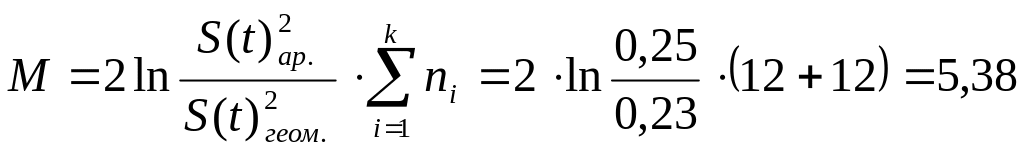его средняя ошибка:

.

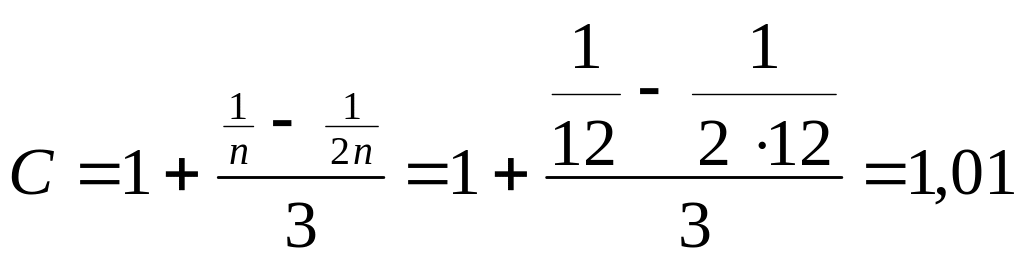M/C=5,32.

Табличное значение при одной степени свободы и значимости 0,05 составляет 3,84. Фактическое значение больше табличного, следовательно, можно считать, что колеблемость в последние 12 лет выше, чем в первые 12 лет изучаемого периода.