Отклонение от линейного тренда

На первом этапе строим линейный тренд и находим от него отклонения «Другие преобразования и графики». В появившемся окне выбираем «Вычесть тренд» (X=X-(a+b*t)) и нажимаем на кнопку «OK (Преобразовать выделенную переменную)». Затем задаем параметры как показано на рисунке 8.15.

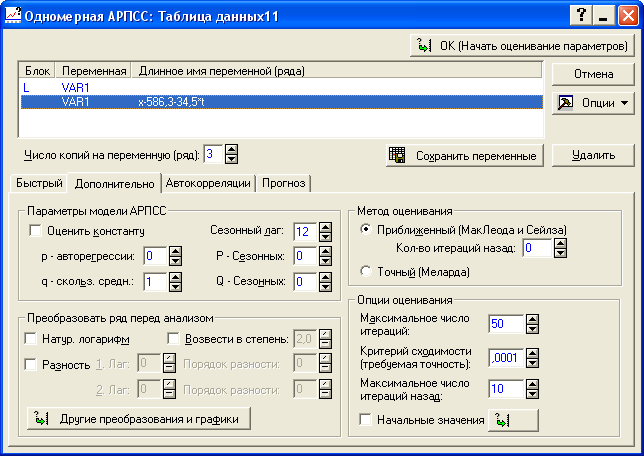
Рисунок 8.15 - Построение модели скользящего среднего по отклонениям от тренда

Результаты оценивания параметров представлены на рисунке 8.16.

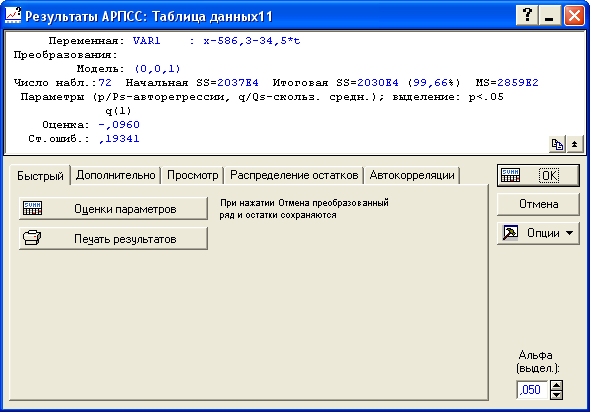
Рисунок 8.16 - Результаты оценивания MA(1) по отклонениям от тренда

Полученная модель имеет вид: .

Откуда (где - расчетные значения по линейному тренду).

При прогнозировании на практике реальные параметры заменяются своими оценками , а случайные шоки - на остатки , полученные при оценивании модели, или на ошибки предыдущих прогнозов.

Для модели MA (1) формулы для прогнозирования имеют вид:

.

В ППП STATISTICA прогнозные значения по полученным моделям можно получить в табличной форме (например, для MA(1) по первым разностям в окне результатов оценивания (рисунок 8.14) на вкладке «Дополнительно» нажав на кнопку «Прогноз») и графической (в том же окне нажав на кнопку «График ряда и прогнозов») соответственно рисунки 8.17 и 8.18.

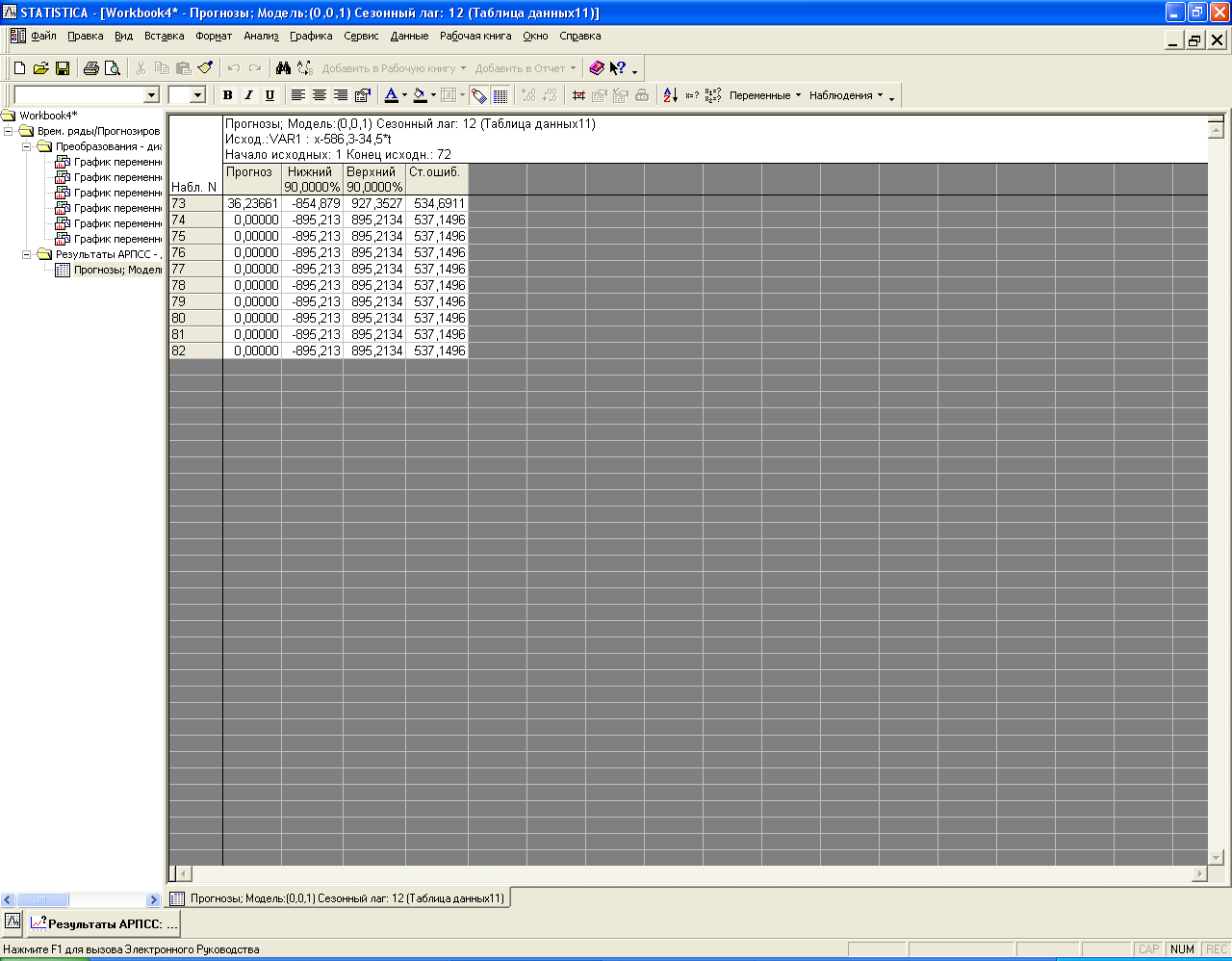
Рисунок 8.17 - Прогноз по MA(1) для первых разностей

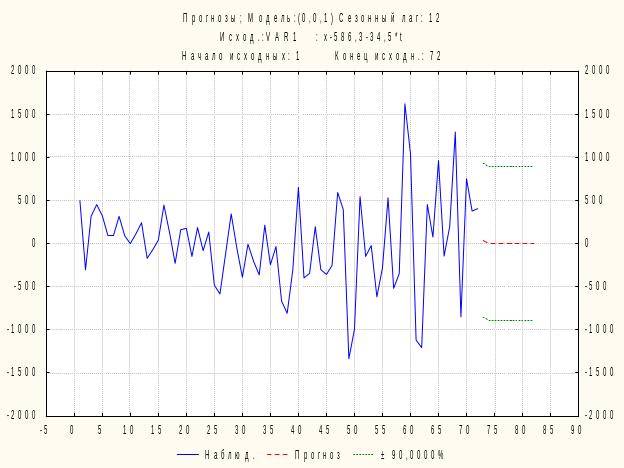
Рисунок 8.18 - Фактические, прогнозные значения и доверительные границы прогноза доходов бюджета Оренбургской области

Построение модели arma (p,q)

Если модель ARMA содержит скользящие средние, то МНК – оценивание, как и в случае с MA- процессами, уже не является возможным. В связи с этим оценивание параметров моделей ARMA в основном проводится по тем же принципам, что и оценивание параметров для МА – процессов, но становится намного сложнее. Например, появляется проблема выбора первоначальных значений из-за наличия регрессоров – лагов зависимой переменной. Наиболее распространенными методами оценивания параметров являются: нелинейный МНК и метод максимального правдоподобия.

Оценим параметры модели ARMA по отклонениям от линейного тренда, используя ППП STATISTICA. Зададим значения параметров как показано на рисунке 8.19.

Таким образом, нами получена модель (рисунок 8.20):

.

Подставим в полученную модель вместо уравнение тренда и после раскрытия скобок и приведения подобных слагаемых перейдем к модели вида:

.

Прогнозные значения отклонений от тренда представлены на рисунке 8.21, их графическое изображение на рисунке 8.22.

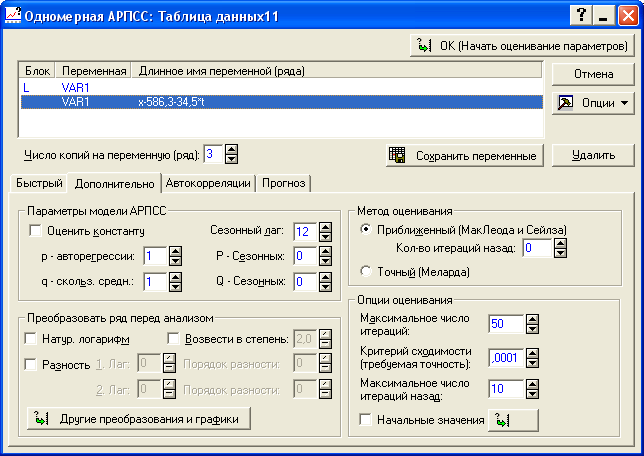
Рисунок 8.19 - Построение ARMA – модели по отклонениям от тренда

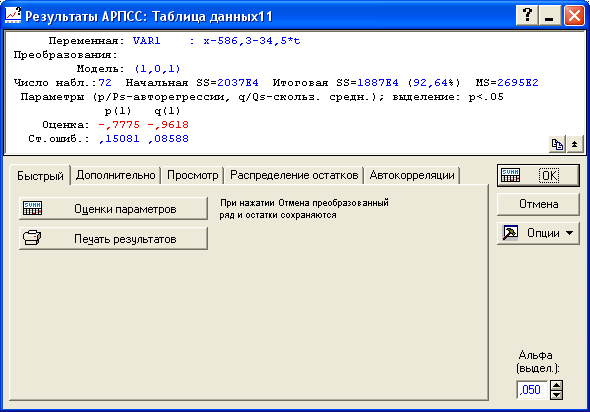
Рисунок 8.20- Результаты оценивания модели ARMA

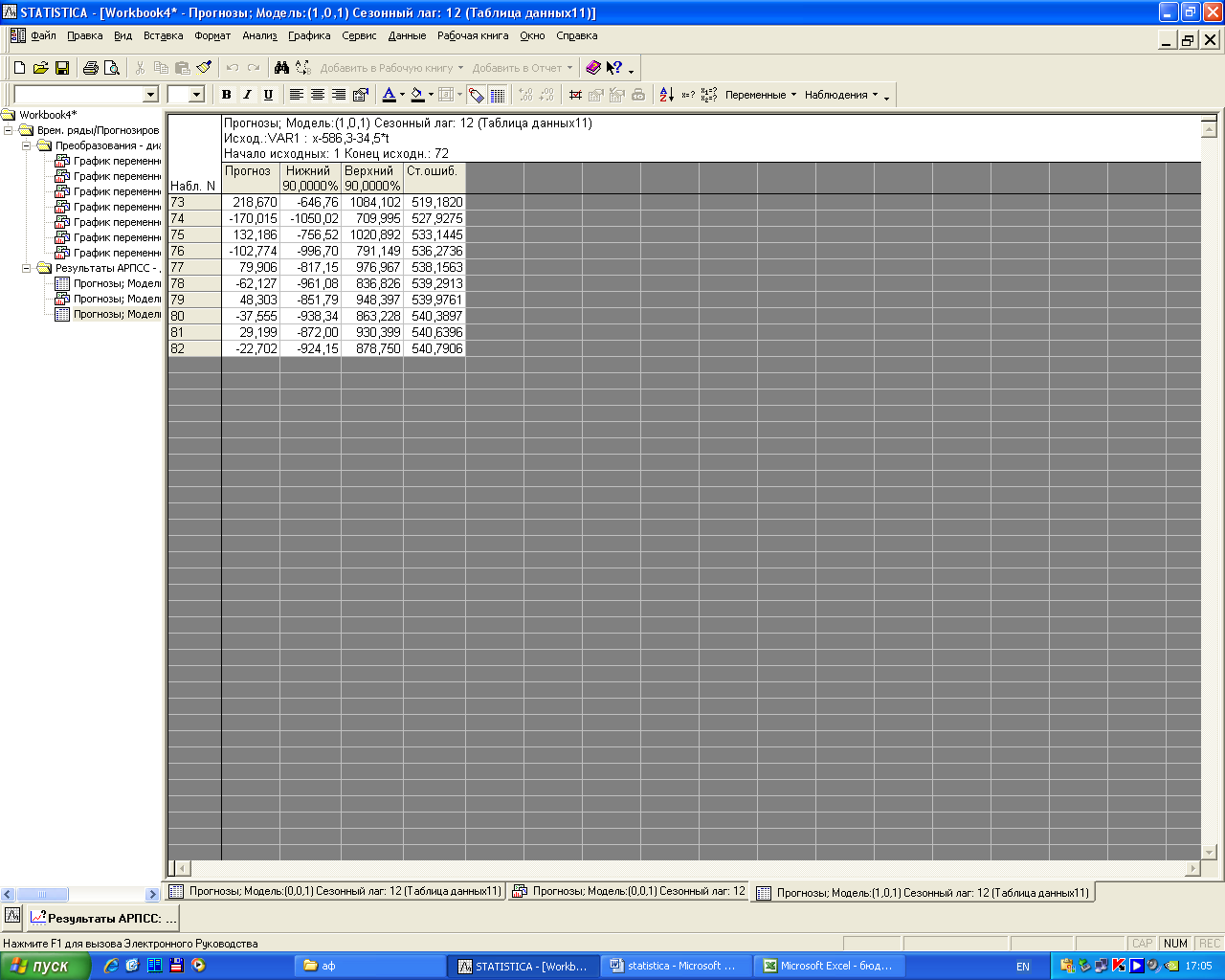
Рисунок 8.21 - Прогноз по модели ARMA(1,1)

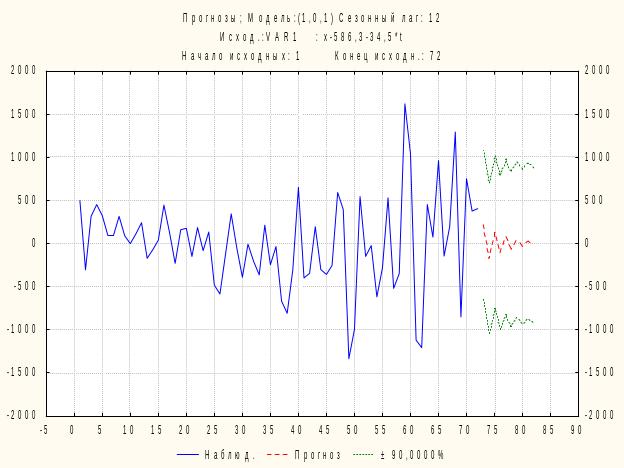
Рисунок 8.22 - Графическое изображение прогноза по модели ARMA(1,1)

Модель ARMA(1,1) по первым разностям представляет собой процесс ARIMA(1,1,1). К построению которой мы и переходим.

Построение модели arima (p,d,q)

Оценим параметры модели в ППП STATISTICA, задав значение параметров, как показано на рисунке 8.23. Результаты оценивания представлены на рисунке 8.24.

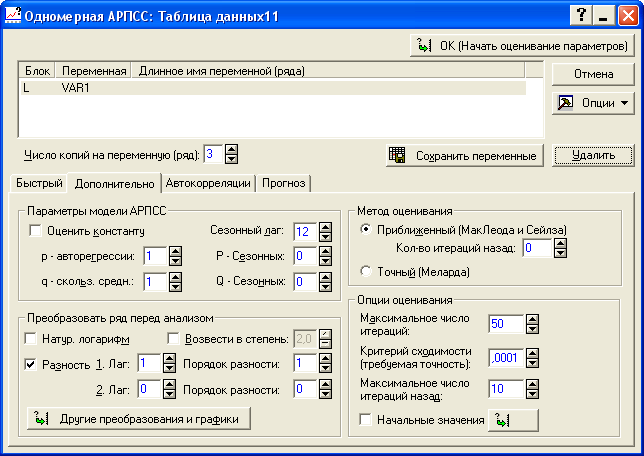
Рисунок 8.23 - Построение ARIMA– модели

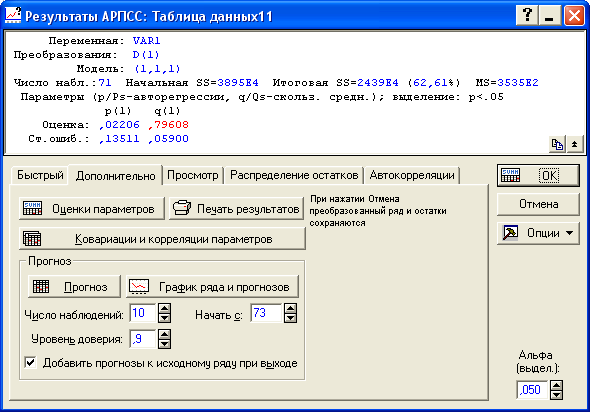
Рисунок 8.24 - Результаты оценивания модели ARIMA

Таким образом, нами получена модель: . Подставив в модель вместо и , раскрыв скобки и приведя подобные слагаемые получим модель: . Рассчитаем по ней теоретические значения доходов бюджета (таблица 8.4).

Как видно на рисунке 8.25, расчетные значения «запаздывают» на 1 месяц по сравнению с фактическими данными. При этом средняя относительная ошибка аппроксимации составила 29,46 %, что свидетельствует об удовлетворительной точности модели.

Прогноз для модели ARIMA(1,1,1) на 1 шаг вперед определяется по формуле:

,

т.е. прогноз на январь 2007 года составит:

млн. р.

На 2 шага вперед: , тогда прогноз на февраль 2007 года составит:

млн.р.

Интервальный прогноз при среднем квадратическом отклонении 763,95 и статистике Стьюдента на 5% уровне значимости для 68 степеней свободы составившей 1,995 для января 2007 года будет находится в границах от 1914,7 млн.р. до 4202,7 млн.р., а в феврале 2007 году доходы бюджета с вероятностью 95 % составит от 1913,8 млн.р. до 4961,8 млн.р.

Таблица 8.4 - Расчет прогноза по модели ARIMA(1,1,1)

Период		Доход, млн.р.		t
1		2		3	4	5	6	7
2001	январь	1119,3		1
	февраль	352,2		2	-767,1	-16,9	14,8
	март	1006,9		3	654,7	14,4	3,5	326,9
	апрель	1177,8		4	170,9	3,8	-2,1	1016,5
	май	1084,4		5	-93,4	-2,1	-4,2	1179,1
	июнь	891,4		6	-193	-4,3	0,9	1086,6
	июль	928,2		7	36,8	0,8	5,5	891,9
	август	1178,4		8	250,2	5,5	-4,3	920,3
	сентябрь	989,4		9	-189	-4,2	-1,2	1186,2
	октябрь	932,2		10	-57,2	-1,3	3,3	989,5
	ноябрь	1080,4		11	148,2	3,3	3,5	931,8
	декабрь	1243,5		12	163,1	3,6	-8,4	1072,4
…	…	…		…	…	…	…	…
2 006	январь	1573	61		-2126,7	-46,9	-0,1	3724,7
	февраль	1521,5	62		-51,5	-1,1	37,4	1563,6
	март	3215,2	63		1693,7	37,4	-8,4	1482,2
	апрель	2872,5	64		-342,7	-7,6	20,5	3279,7
	май	3792,4	65		919,9	20,3	-24,1	2824,6
	июнь	2721,7	66		-1070,7	-23,6	8,8	3840,7
	июль	3097,2	67		375,5	8,3	24,8	2715,9
	август	4229,2	68		1132	25,0	-47,1	3038,7

Продолжение таблицы 8.4

1		2		3	4	5	6	7
	сентябрь	2119,6	69		-2109,6	-46,5	37,1	4328,8
	октябрь	3756,5	70		1636,9	36,1	-8,3	2035,2
	ноябрь	3416,1	71		-340,4	-7,5	1,5	3800,8
	декабрь	3478,7	72		62,6	1,4	52,0	3459,4
Итого		132968,7	-		2359,4	52,0	119,9	128472,4
В среднем		1846,7875	-		32,769444	0,7	1,7	1835,3

Рисунок 8.25 - Динамика доходов бюджета Оренбургской области