7 Лабораторная работа 3
Использование адаптивных методов прогнозирования в экономических исследованиях
Цель изучения темы: научиться задавать значение параметра адаптации в зависимости от целей прогнозирования. Строить адаптивные модели для стационарных и нестационарных временных рядов. Оценивать точность полученных моделей.
Контрольные вопросы
1 Укажите характерные особенности адаптивных методов прогнозирования.
2 Какие типы адаптивных моделей вы знаете?
3 Чем объясняется название «экспоненциальная средняя»?
4 Какую роль играет параметр адаптации в процедуре экспоненциального сглаживания?
5 Как влияет значение параметра адаптации на характер ряда, полученного после экспоненциального сглаживания?
Задания
1 По данным лабораторной работы 1 постройте адаптивную модель. В качестве начального значения экспоненциальной средней возьмите средний уровень ряда. Дайте прогноз на следующий год.
2 По данным лабораторной работы 1 постройте адаптивную полиномиальную модель. Дайте прогноз на следующий год.
Решение типовых задач
Для данных о доходах консолидированного бюджета Оренбургской области (таблица 7.1) рассчитаем экспоненциальную среднюю. В качестве начального значения экспоненциальной средней возьмем среднее значение из пяти первых уровней ряда параметр адаптации примем = 0,5.
Определим
948,12
Найдем значение экспоненциальной средней при = 0,5.
…
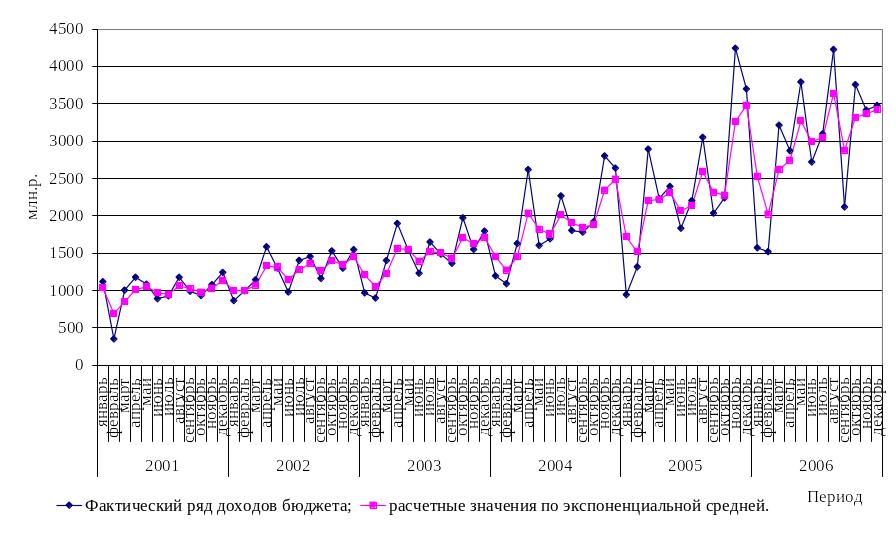
На рисунке 7.1 представлены результаты расчетов и динамика исходного временного ряда.
Таблица 7.1 - Значения доходов консолидированного бюджета Оренбургской области, млн.р.
Период |
1 |
2 |
3 |
4 |
5 |
6 |
январь |
1119,3 |
865,5 |
968,8 |
1196,8 |
944,1 |
1573 |
февраль |
352,2 |
998,4 |
900 |
1091,1 |
1317,3 |
1521,5 |
март |
1006,9 |
1145,1 |
1402 |
1629,4 |
2893,2 |
3215,2 |
апрель |
1177,8 |
1585,6 |
1898,8 |
2620,2 |
2234,3 |
2872,5 |
май |
1084,4 |
1301 |
1538,8 |
1603,7 |
2393,7 |
3792,4 |
июнь |
891,4 |
980,3 |
1232,7 |
1692,8 |
1834,2 |
2721,7 |
июль |
928,2 |
1403,5 |
1650,1 |
2267,5 |
2205,4 |
3097,2 |
август |
1178,4 |
1455,7 |
1486,9 |
1804,6 |
3051,7 |
4229,2 |
сентябрь |
989,4 |
1163,5 |
1364,3 |
1782,8 |
2035,7 |
2119,6 |
октябрь |
932,2 |
1532 |
1974,6 |
1921 |
2241,3 |
3756,5 |
ноябрь |
1080,4 |
1299,9 |
1551,1 |
2802,3 |
4245,3 |
3416,1 |
декабрь |
1243,5 |
1549,1 |
1795,6 |
2639,6 |
3699,7 |
3478,7 |
Как видно на графике расчетные значения близки к исходному временному ряду, ошибка аппроксимации составила 14,57 %. Это свидетельствует о хорошей точности модели.
Спрогнозируем доходы бюджета на январь 2007 года по формуле:
млн.р.
Адаптивное прогнозирование по полиномиальным моделям
По данным таблицы 7.1 рассчитаем прогноз по адаптивным полиномиальным моделям.
Увеличим
значение параметра адаптации с целью
придания большего веса последним
наблюдениям:
.
Применим аналитическое выравнивание
в виде полиномиального тренда 1-го
порядка. Уравнение тренда примет вид:
.
Тогда
;
.
Находим начальные значения экспоненциальных средних:
,
.
Экспоненциальные средние составят:
,
где
.
,
.
Р
исунок
7.1 - Экспоненциальное сглаживание
временного ряда доходов бюджета
Находим оценки коэффициентов модели (скорректированные параметры линейного тренда):
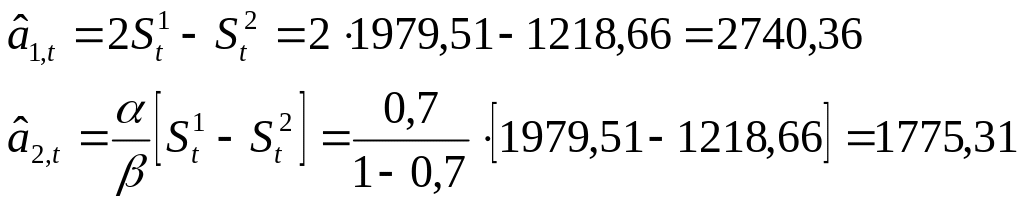
Осуществляем прогноз на одну точку вперед:
млн.р.
Экспоненциальное сглаживание в ППП STATISTICA
Выберем значение параметра адаптации используя перебор по сетке значений. Стандартным образом запустите модуль «Временные ряды и прогнозирование» (рисунок 7.2).
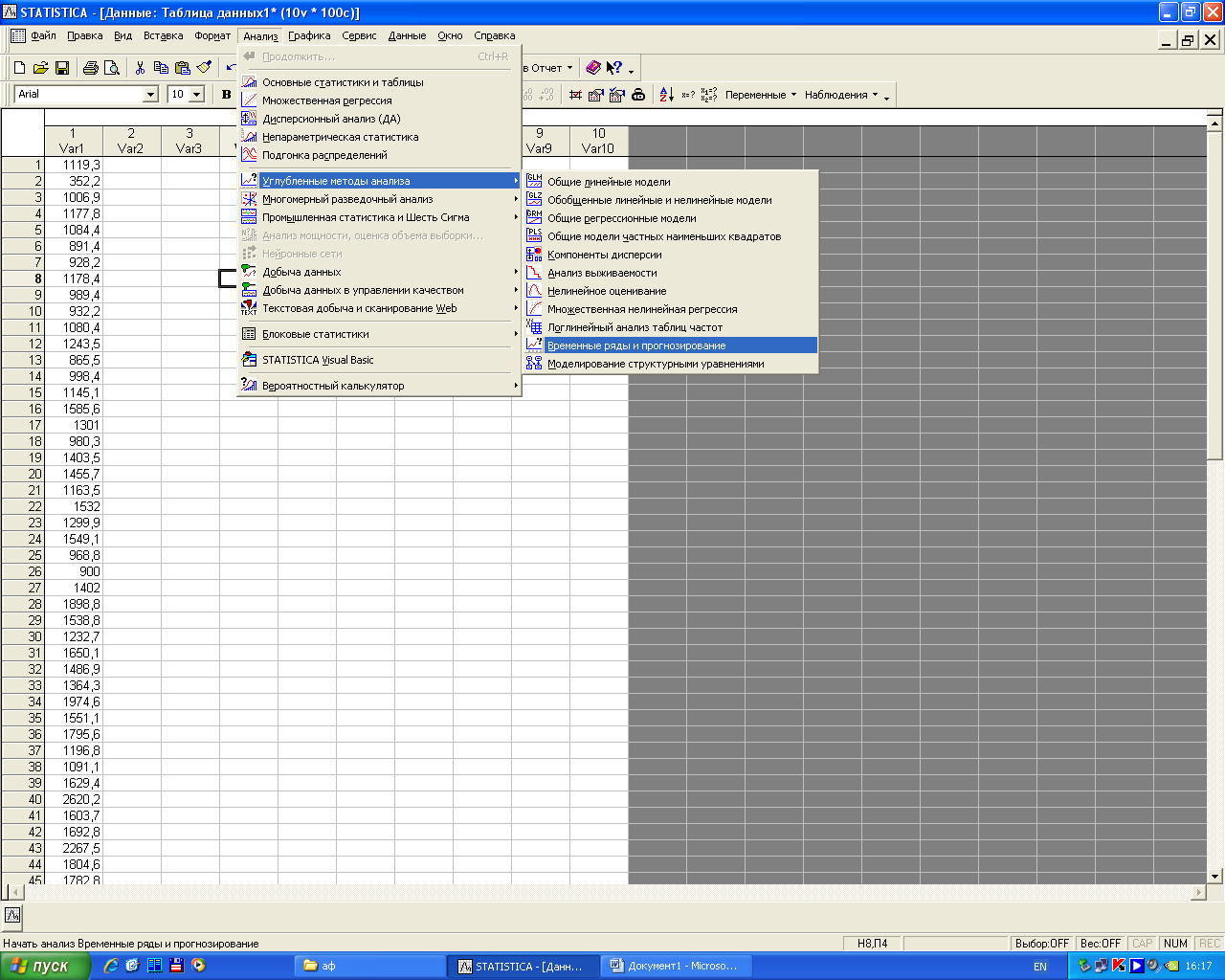
Рисунок 7.2 - Запуск модуля «Временные ряды и прогнозирование»
В появившемся окне выбираем «Экспоненциальное сглаживание и прогноз» и задаем переменную в окне «Переменные» (рисунок 7.3).
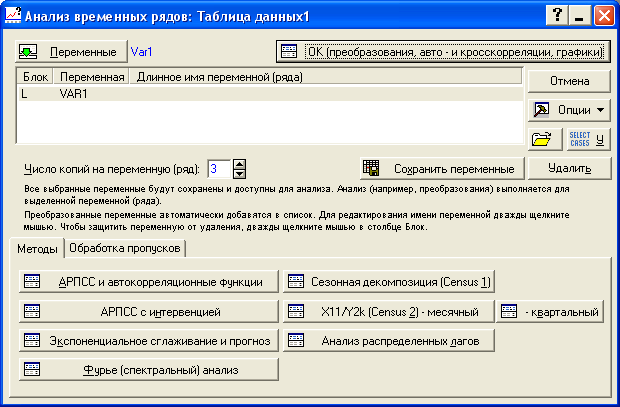
Рисунок 7.3 - Диалоговое окно «Временные ряды и прогнозирование»
В появившемся диалоговом окне выбираем вкладку «Поиск на сетке» (рисунок 7.4).
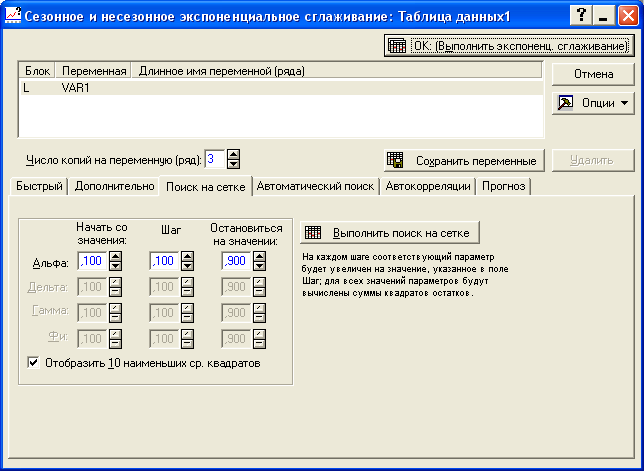
Рисунок 7.4 - Диалоговое окно экспоненциального сглаживания
По умолчанию перебор осуществляется с начального значения = 0,100 до =0,900 с шагом 0,100 (данные значения можно менять). В результате выводится 10 наилучших значений . Если необходимо просмотреть все значения , то необходимо убрать метку в строке «Отобразить 10 наименьших ср.квадратов».
Для просмотра сетки значений необходимо нажать кнопку «Выполнить поиск на сетке». По анализируемым данным наилучшим значением для параметра адаптации является =0,2, при нем наблюдаются наименьшие значения суммы квадратов отклонений (рисунок 7.5).
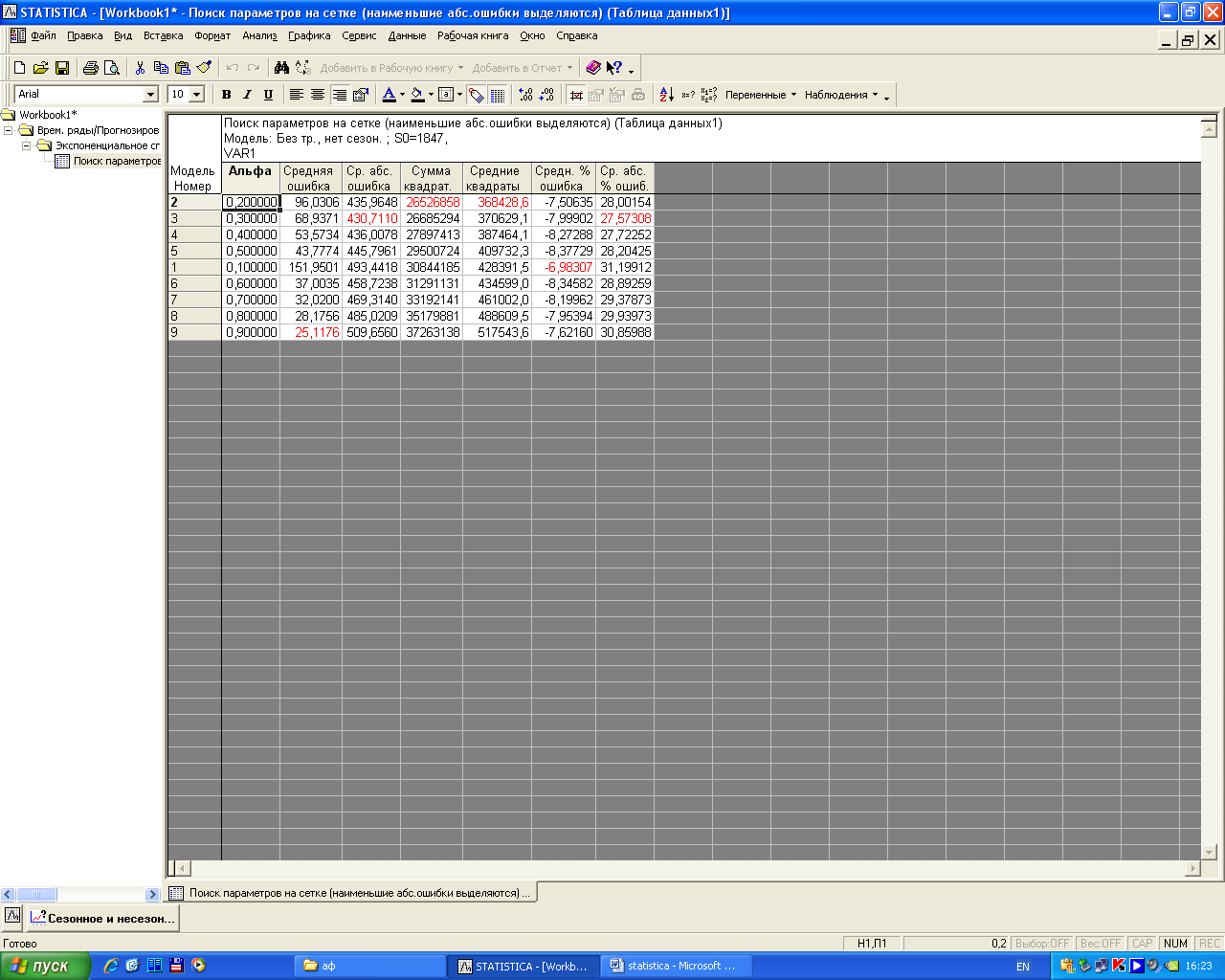
Рисунок 7.5 - Сетка значений для выбора
В
качестве начального значения
экспоненциальной средней берется
средняя арифметическая простая из всех
уровней временного ряда, которая для
анализируемого ряда составила
.
Адаптивная модель примет вид:
.
Чтобы рассчитать ряд экспоненциальных
средних и прогноз на следующий период,
в диалоговом окне экспоненциального
сглаживания необходимо выбрать вкладку
«Дополнительно» сделать установки как
показано на рисунке 7.6 и нажать на кнопку
«ОК: (Выполнить экспоненциальное
сглаживание)». В результате появится
окно, содержащее значения экспоненциальной
средней и прогноз на 10 шагов (рисунок
7.7).
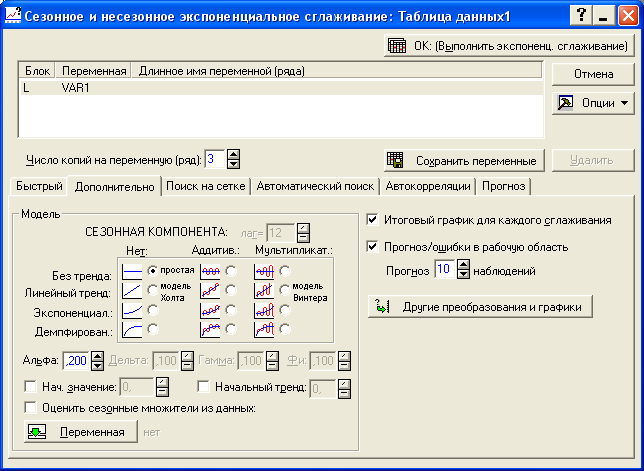
Рисунок 7.6 - Задание параметров для экспоненциального сглаживания
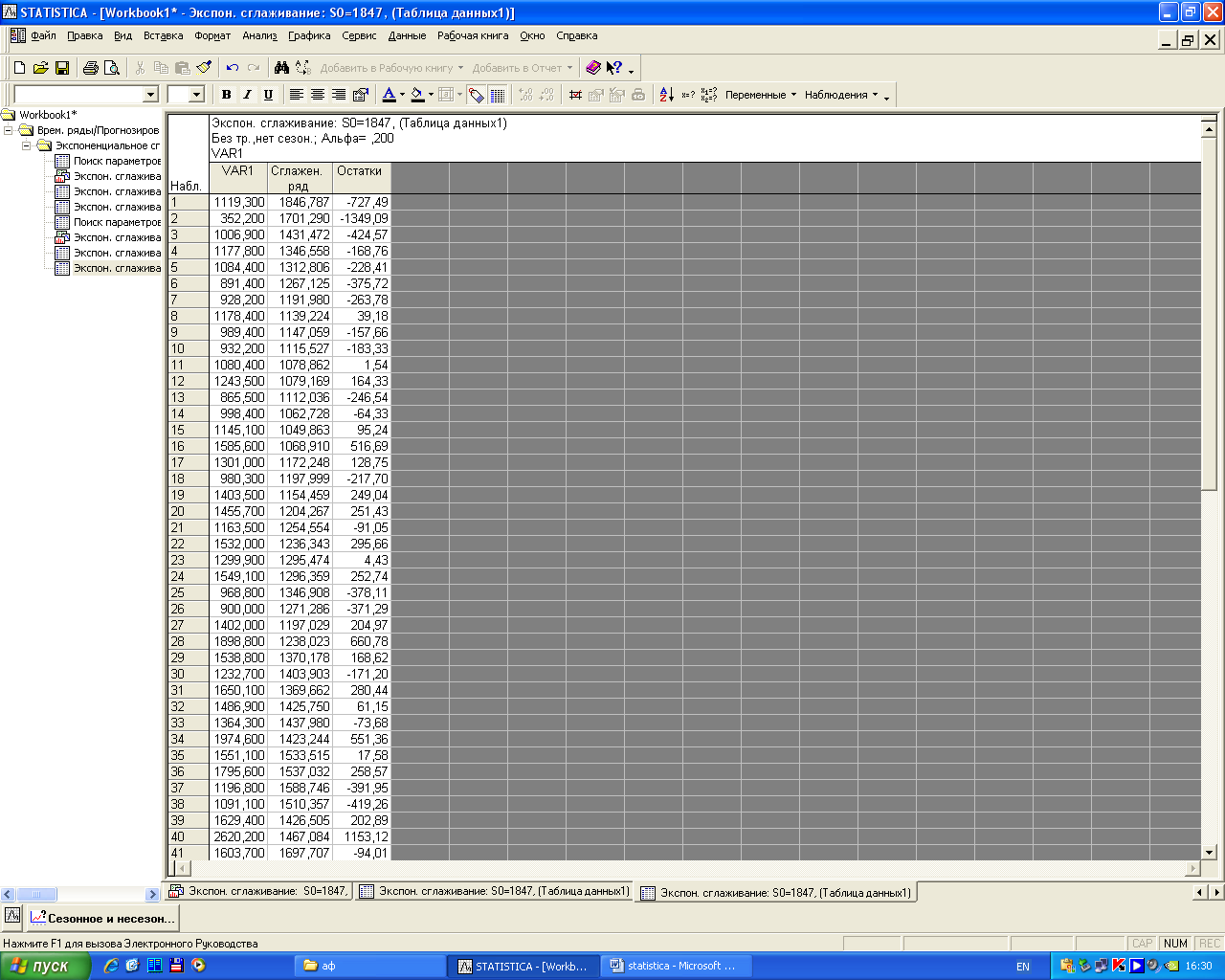
Рисунок 7.7 - Результаты экспоненциального сглаживания
и прогнозирования