Прогнозирование по модели регрессии с включением фактора времени и фиктивных переменных
Спрогнозируем объем производства с помощью модели регрессии с включением фактора времени и фиктивных переменных. Модель для помесячной динамики имеет вид:
где
.
.
.
Занесем значение фиктивных переменных и фактора времени в таблицу (таблица 6.8).
Таблица 6.8 - Исходные данные для расчета параметров уравнения регрессии с фиктивными переменными во временном ряду доходов бюджета, (млн.р.)
Период |
Доход, млн.р. |
t |
x1 |
x2 |
… |
x10 |
x11 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
январь |
1119,3 |
1 |
1 |
0 |
|
0 |
0 |
124,4 |
февраль |
352,2 |
2 |
0 |
1 |
|
0 |
0 |
43,3 |
|
март |
1006,9 |
3 |
0 |
0 |
|
0 |
0 |
895,2 |
|
апрель |
1177,8 |
4 |
0 |
0 |
|
0 |
0 |
1078,1 |
|
май |
1084,4 |
5 |
0 |
0 |
|
0 |
0 |
965,5 |
|
июнь |
891,4 |
6 |
0 |
0 |
|
0 |
0 |
572,0 |
|
июль |
928,2 |
7 |
0 |
0 |
|
0 |
0 |
938,5 |
|
август |
1178,4 |
8 |
0 |
0 |
|
0 |
0 |
1214,3 |
|
сентябрь |
989,4 |
9 |
0 |
0 |
|
0 |
0 |
589,1 |
|
октябрь |
932,2 |
10 |
0 |
0 |
|
1 |
0 |
1072,8 |
|
ноябрь |
1080,4 |
11 |
0 |
0 |
|
0 |
1 |
1412,4 |
|
декабрь |
1243,5 |
12 |
0 |
0 |
|
0 |
0 |
1414,2 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
Продолжение таблицы 6.8
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
6 |
январь |
1573 |
61 |
1 |
0 |
|
0 |
0 |
2098,1 |
февраль |
1521,5 |
62 |
0 |
1 |
|
0 |
0 |
2016,9 |
|
март |
3215,2 |
63 |
0 |
0 |
|
0 |
0 |
2868,8 |
|
апрель |
2872,5 |
64 |
0 |
0 |
|
0 |
0 |
3051,7 |
|
май |
3792,4 |
65 |
0 |
0 |
|
0 |
0 |
2939,1 |
|
июнь |
2721,7 |
66 |
0 |
0 |
|
0 |
0 |
2545,7 |
|
июль |
3097,2 |
67 |
0 |
0 |
|
0 |
0 |
2912,1 |
|
август |
4229,2 |
68 |
0 |
0 |
|
0 |
0 |
3187,9 |
|
сентябрь |
2119,6 |
69 |
0 |
0 |
|
0 |
0 |
2562,7 |
|
октябрь |
3756,5 |
70 |
0 |
0 |
|
1 |
0 |
3046,4 |
|
ноябрь |
3416,1 |
71 |
0 |
0 |
|
0 |
1 |
3386,0 |
|
декабрь |
3478,7 |
72 |
0 |
0 |
|
0 |
0 |
3387,8 |
|
7* |
январь |
- |
73 |
1 |
0 |
|
0 |
0 |
2492,8 |
февраль |
- |
74 |
0 |
1 |
|
0 |
0 |
2411,6 |
|
март |
- |
75 |
0 |
0 |
|
0 |
0 |
3263,5 |
|
апрель |
- |
76 |
0 |
0 |
|
0 |
0 |
3446,4 |
|
Оценим параметры уравнения традиционным МНК с помощью табличного редактора Excel (таблица 6.9).
Уравнение регрессии примет вид:
.
Параметры
,
характеризуют отклонения уровней
временного ряда от уровней, учитывающих
сезонные воздействия в декабре. Величина
параметра
говорит о том, что в среднем за месяц
происходит увеличение доходов бюджета
на 32,89 млн.р. (рисунок 6.5).
Таблица 6.9 - Результаты оценивания регрессионной модели
с фиктивными переменными
Регрессионная статистика |
||||||
Множественный R |
0,894765 |
|||||
R-квадрат |
0,800604 |
|||||
Нормированный R-квадрат |
0,760049 |
|||||
Стандартная ошибка |
440,6634 |
|||||
Наблюдения |
72 |
|||||
Дисперсионный анализ |
||||||
|
df |
SS |
MS |
F |
Значимость F |
|
Регрессия |
12 |
46001035 |
3833420 |
19,74 |
0,000 |
|
Продолжение таблицы 6.9
Остаток |
59 |
11456867 |
194184,2 |
|
|
||||||
Итого |
71 |
57457903 |
|
|
|
||||||
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
|||||
a |
1019,50 |
209,02 |
4,88 |
0,00 |
601,24 |
1437,75 |
|||||
b |
32,89 |
2,53 |
12,98 |
0,00 |
27,82 |
37,96 |
|||||
c1 |
-927,95 |
255,94 |
-3,63 |
0,00 |
-1440,09 |
-415,82 |
|||||
c2 |
-1042,01 |
255,68 |
-4,08 |
0,00 |
-1553,62 |
-530,41 |
|||||
c3 |
-223,02 |
255,44 |
-0,87 |
0,39 |
-734,15 |
288,11 |
|||||
c4 |
-73,02 |
255,22 |
-0,29 |
0,78 |
-583,72 |
437,68 |
|||||
c5 |
-218,44 |
255,03 |
-0,86 |
0,40 |
-728,77 |
291,88 |
|||||
c6 |
-644,82 |
254,87 |
-2,53 |
0,01 |
-1154,82 |
-134,83 |
|||||
c7 |
-311,25 |
254,73 |
-1,22 |
0,23 |
-820,97 |
198,47 |
|||||
c8 |
-68,38 |
254,62 |
-0,27 |
0,79 |
-577,87 |
441,12 |
|||||
c9 |
-726,47 |
254,53 |
-2,85 |
0,01 |
-1235,78 |
-217,15 |
|||||
c10 |
-275,65 |
254,47 |
-1,08 |
0,28 |
-784,83 |
233,54 |
|||||
c11 |
31,04 |
254,43 |
0,12 |
0,90 |
-478,07 |
540,16 |
|||||
Чтобы получить прогнозные значения доходов бюджета на следующие 4 месяца 7 года необходимо в уравнение регрессии подставить следующие значения фактора времени t.
Так прогноз на январь составит:
на февраль:
на
март:
на апрель:
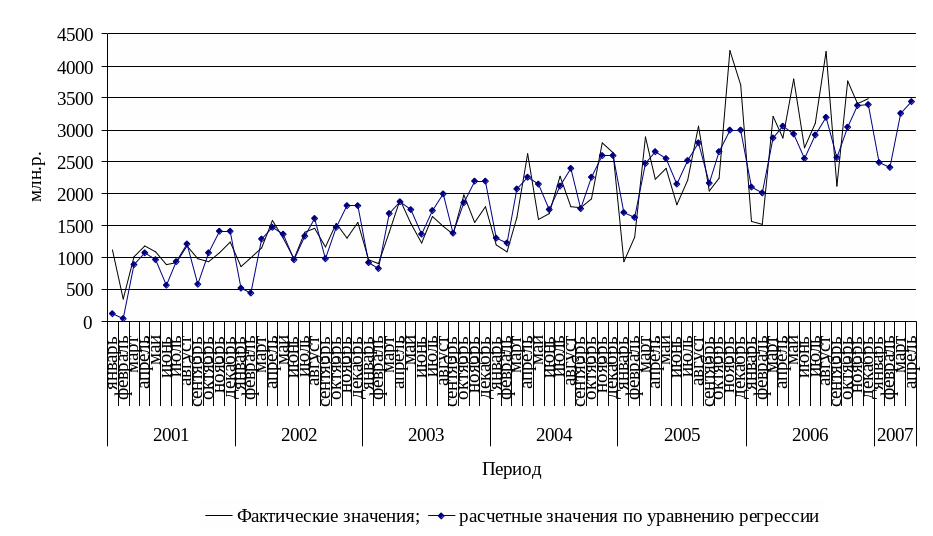
Р исунок 6.5 - Моделирование сезонных колебаний доходов бюджета с помощью фиктивных переменных