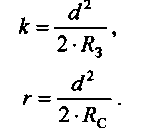- •IV. Тахеометричне знімання
- •IV.1. Основні формули та прилади тахеометричного знімання
- •IV. 1.1. Суть тахеометричного знімання
- •IV. 1.3. Нитковий віддалемір. Теорія ниткового віддалеміра у трубі із зовнішнім фокусуванням
- •IV.1.4. Визначення сталих к і с ниткового віддалеміра
- •IV. 1.5. Теорія ниткового віддалеміра в трубі з внутрішнім фокусуванням
- •IV.1.6. Експериментальне визначення змінної Рт
- •IV.1.7. Тахеометричні рейки
- •IV. 1.8. Приведення похилих віддалей, виміряних нитковим віддалеміром, до горизонту
- •IV. 1.9. Перетворення основної формули тригонометричного нівелювання
- •IV. 1.10. Точність тригонометричного нівелювання
- •IV.1.11. Точність ниткового віддалеміра
- •IV.1.12. Будова вертикального круга тахеометра з циліндричним рівнем при алідаді вертикального круга
- •IV.1.13. Будова вертикального круга тахеометра з циліндричним рівнем тільки при алідаді горизонтального круга
- •IV.1.14. Виведення формул для визначення місця нуля (мо) і кутів нахилу тахеометром 2т-30
- •IV. 1.15. Виведення формул для визначення місця нуля (мо) і кутів нахилу тахеометра т-30
- •IV. 1.16. Приведення значення місця нуля (мо) до нуля
- •IV.1.17. Перевірки кругових тахеометрів
- •IV. 1.18. Будова номограм ного тахеометра
- •IV.1.19. Теорія номограмного тахеометра
- •IV.1.20. Перевірка номограмного тахеометра
- •IV. 1.21. Електронні тахеометри та автоматизовані системи відлічування
- •IV. 1.22. Будова електронного тахеометра Leica тс 403l
- •IV.2. Виконання тахеометричного знімання поверхні
- •IV.2.1. Знімальна основа для тахеометричного знімання
- •IV.2.2. Створення пунктів знімальної основи тахеометричними ходами
- •IV.2.5. Прокладання тахеометричного ходу
- •IV.2.7. Послідовність роботи на станції під час тахеометричного знімання
- •IV.3. Камеральні роботи за результатами тахеометричного знімання
- •IV.3.1. Опрацювання журналу тахеометричного ходу
- •IV.3.3. Обчислення висот пунктів тахеометричного ходу
- •IV.3.4. Опрацювання журналу тахеометричного знімання
- •IV.3.5. Складання плану тахеометричного знімання
Якщо
горизонтальне знімання дає змогу
визначати планове, а геометричне
нівелювання - висотне положення точок
місцевості, то за допомогою тахеометричного
знімання можна одночасно встановити
як планове, так і висотне положення цих
точок.
В
основу тахеометрії покладено ідею, що
полягає в тому, щоб отримати просторове
положення точки місцевості одним
візуванням (наведенням) труби приладу
на цю точку. Виконуючи таке візування,
вимірюють віддаль від тахеометра до
точки, горизонтальний та вертикальний
кути.
Слово
“тахеометрія” дослівно означає швидке
вимірювання, швидке знімання.
Вдосконаливши процес вимірювання
ліній, вдалось зробити швидшим
тахеометричне знімання. Саме завдяки
застосуванню віддалемірів зросла
продуктивність праці, ефективність і
якість знімальних робіт. З появою
електронних тахеометрів з’явилась
можливість повністю автоматизувати
як польові, так і камеральні роботи.
Фактично
під час виконання тахеометричного
знімання планове положення точок
визначають переважно полярним методом,
а висотне - нівелюванням нахиленим
візирним променем, яке називають
тригонометричним
нівелюванням.
Нехай
над точкою 1 з відомими координатами
зцентровано тахеометр, а лімб тахеометра
встановлено горизонтально і зорієнтовано
за напрямком 1-2 (рис.
IV.
1.1).
Зорієнтувати
тахеометр
за деяким напрямком (наприклад, 1-2)
означає встановити горизонтальний
круг (лімб) приладу так, щоб, у разі
наведення зорової труби на точку 2,
відлік горизонтального круга дорівнював
0°00,0'. Значення поділок на крузі
збільшуються за ходом годинникової
стрілки від 0° до 360°.
Нехай
на місцевості маємо точки 11, 12, 13, ... 1і
(перша цифра означає номер пункта,
над
яким встановлено тахеометр, друга -
порядковий номер точки), планове
положення якої потрібно визначити. Для
цього над нею встановлюють тахеометричну
рейку (можна нівелірну). Тому таку точку
називають рейковою, або, як у нівелюванні,
пікетною.
314IV. Тахеометричне знімання
IV.1. Основні формули та прилади тахеометричного знімання
IV. 1.1. Суть тахеометричного знімання
Тахеометричне
знімання
-Ф-2
Встановивши
лімб нерухомо, відкріп-
люють алідаду
і наводять вертикальною
ниткою
(центром бісектора) сітки ниток
зорову
трубу на рейку, розміщену в точці 11.
Відлічують
горизонтальний круг. Відлік
дорівнюватиме
куту j8„.
Віддал еміром вимі-
рюють віддаль
5П
і обчислюють її гори-
зонтальну
проекцію dn.
Цих даних достат-
ньо, щоб на папір,
де вже позначено станції
(пункти 1
та 2), нанести шукану точку 11.
Справді,
якщо за допомогою транспортира
відкласти
кут /3,,, а вздовж цього напрямку в
масштабі
плану від пункта
1
відкласти від-
даль то отримаємо на
плані положення
пікетної
точки 11. Аналогічно визначають положення
точок 12, 13,..., 1і. Тепер
залишається
знайти висоти пікетів 11, 12, 13,..., 1і. Для
цього достатньо знайти
перевищення
цих пікетів відносно висоти тахеометра
на станції 1.
Рис.
IV.
1.1. Визначення полярним методом планового
положення точки 11
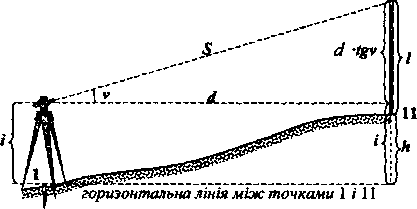
Рис.
IV.
1.2. Визначення перевищення між точками
з тригонометричного нівелювання
Пояснимо
суть визначення перевищення нахиленим
променем (тригонометричним
нівелюванням). На рис.
IV.
1.2
показано вертикальний розріз місцевості
по лінії 1-11. Над точкою 1 центрують
тахеометр, трубу якого наведено на
відлік рейки 1.
Рейку встановлено вертикально на пікеті
11. Рулеткою вимірюють висоту тахеометра.
Висотою
тахеометра
(приладу) називають висоту осі обертання
зорової труби над точкою 1. Її позначають
буквою і.
Довжину лінії від тахеометра до точки
вимірюють відцалеміром. Відлічують
вертикальний круг тахеометра і обчислюють
кут нахилу V,.. Достатньо, як і для
вимірювання горизонтальних кутів Д.,
відлічити
один раз вертикальний круг теодоліта
при КЛ.
315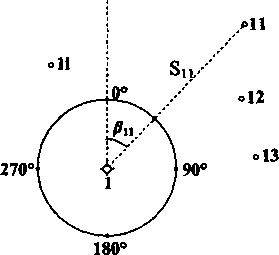
Розділ
IV
З
трикутника INM
маємо:
MN
=
d
•
tgv.
Безпосередньо з рис.
IV.
1.2
можна записати геометричне співвідношення:
h
+ l
= d
•
tgv
+
і.
Звідси
h
= d-tgv
+ i-l. (IV.1.1)
Висоту
точки 11 Нп
можна визначити за формулою
Hn=H}+h, (IV.
1.2)
де
Я, - висота точки, над якою встановлено
тахеометр (висота станції).
Отже,
для визначення висот з тригонометричного
нівелювання потрібно знати значення
вертикальних кутів (кутів нахилу) і
горизонтальні довжини ліній. Останні
необхідні й для визначення планового
положення точок.
Аналогічно
знаходять висоти інших пікетів.
Зауважимо, що, володіючи добрими
практичними навичками, виконавець з
одного наведення труби миттєво зчитує
з рейки віддаль St
та
відліки горизонтального та вертикального
v;
кругів.
За цими параметрами можна отримати
просторові значення координат (X,
Y,
Н)
шуканої точки.
IV.
1.2. Виведення повної формули
тригонометричного нівелювання
Формула
(IV. 1.1) не враховує кривини Землі та
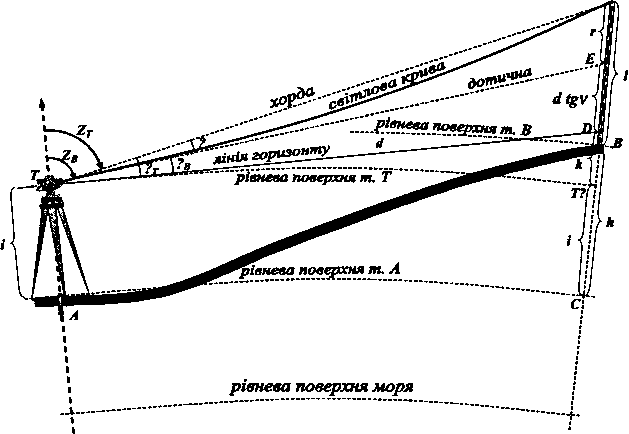
вертикальної рефракції. Розглянемо,
як зміниться ця формула, якщо взяти до
уваги ці два явища. Наше завдання -
визначити перевищення h
=
ВС
(рис. IV.
1.3)
як прямовисну віддаль між рівневими
поверхнями, що проходять через точки
А
та В
і паралельні до рівневої поверхні моря.
Нехай висота наведення дорівнює /.
Візуємо на рейку в точку F.
В неоднорідній за густиною атмосфері
світло поширюється не прямолінійно, а
по кривій, модель якої показана на рис.
IV.
1.3
потовщеною кривою. Як тільки труба буде
спрямована по дотичній ТЕ
в точці Т,
то спостерігач побачить F.
Висота
приладу АТ
= СТ' = і.
Вимірюємо вертикальний кут vB
між
дотичною до кривої поширення світла
ТЕ
та дотичною TD
до
рівневої поверхні в точці Т.
Знаючи горизонтальну віддаль TD
= d
між
точками А
і В,
що нівелюють, визначаємо відрізок ED.
У трикутнику TED
кут
в точці D
майже
не відрізняється від прямого, тому цей
трикутник приймемо за прямокутний.
Звідси: ED
=
d
•
tgv
.
Відрізок DT'
і
є вплив кривини Землі. З рис.
IV.
1.3
видно, що
h
+ l
= d
■
tgv
+ i
+ k
+ r. (IV.
1.3)
Звідси
h
= d-tgv
+ i-l + k + r. (IV.
1.4)
Позначимо
316
Тахеометричне
знімання
k
+ r
= f, (TV.
1.5)
де /
- сумісний
вплив кривини Землі та вертикальної
рефракції.
Ввівши це позначення у формулу (IV. 1.4),
отримаємо
h
= d-tgv
+
І-1 + f. (IV.
1.6)
Формула (IV. 1.6) є повною формулою
тригонометричного нівелювання, і
відрізняється від (IV. 1.1) тільки членом
/.
Вплив кривини Землі к
і
вертикальної рефракції г
виражається
співвідношеннями:
Рис.
IV.1.3.
До
виведення повної формули тригонометричного
нівелювання
317
У формулах (IV. 1.7) та (IV. 1.8)
R3
- радіус Землі, Rc
- радіус кривої рефракції
(кривої поширення світла) .
Зауважимо, що в приземних
прошарках атмосфери вертикальні
градієнти температури змінюються у
великих межах і на висоті 1 м можуть
досягти ±1 град/м
і більше. Тому г
є величиною змінною, і це основна
причина, яка знижує точність
тригонометричного нівелювання.