26

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИНСТИТУТ ЭНЕРГЕТИЧЕСКОГО МАШИНОСТРОЕНИЯ

КАФЕДРА ФИЗИКИ

Электростатика

методические указания к самостоятельной работе

по физике (раздел «Электричество и магнетизм»)

Ростов-на-Дону 2012

Составители: Н.В.Дорохова, В.П.Сафронов, В.В Шегай

УДК 537.8

Электростатика. Метод. указания. - Ростов н/Д: Издатель­ский центр ДГТУ, 2012 , 24 с.

Указания содержат краткие теоретические сведения по теме «Электростатика», примеры решения задач и задачи для самостоятельного решения.

Методические указания предназначены для выполнения самостоятельных работ по физике студентами ИЭМ технических специальностей всех форм обучения (раздел «Электричество и магнетизм»).

Печатается по решению методической комиссии факультета «Н и КМ»

Научный редактор доц. Ковалева В.С.

©, Н.В.Дорохова, В.П.Сафронов, В.В Шегай, 2012

© Издательский центр ДГТУ, 2012

Оглавление

1.	Краткая теория	3
2.	Примеры решения задач	5
3.	Задачи для самостоятельного решения	13
4.	Справочные материалы	23
5.	Варианты типовых заданий	24
6.	Литература	24

Краткая теория

Закон Кулона:

,

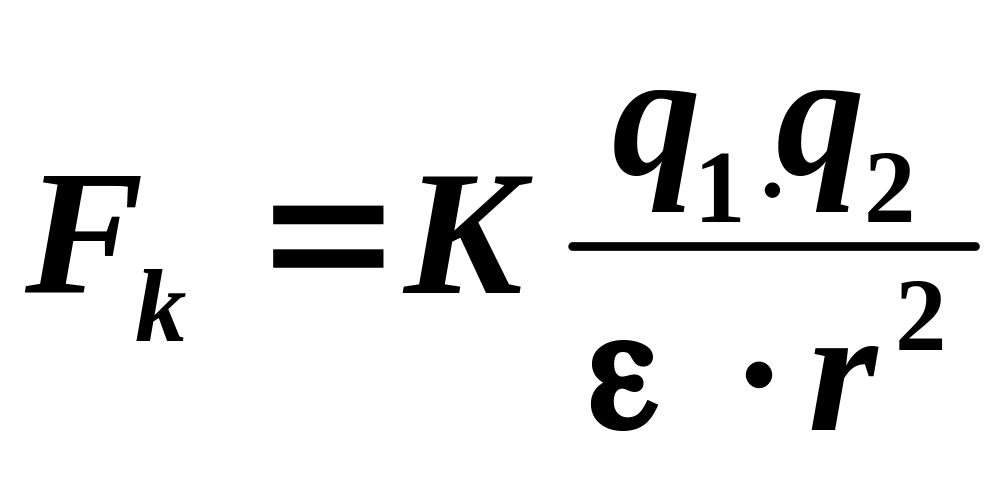где q₁, q₂ - точечные заряды; [q] = Кл.

— коэффициент в Си;

ε_0= 8,85^.10^-12 Кл²/ (Н^.м²) — электрическая постоянная;

ε— диэлектрическая проницаемость среды;

r — расстояние между зарядами.

Напряженность электрического поля:

;

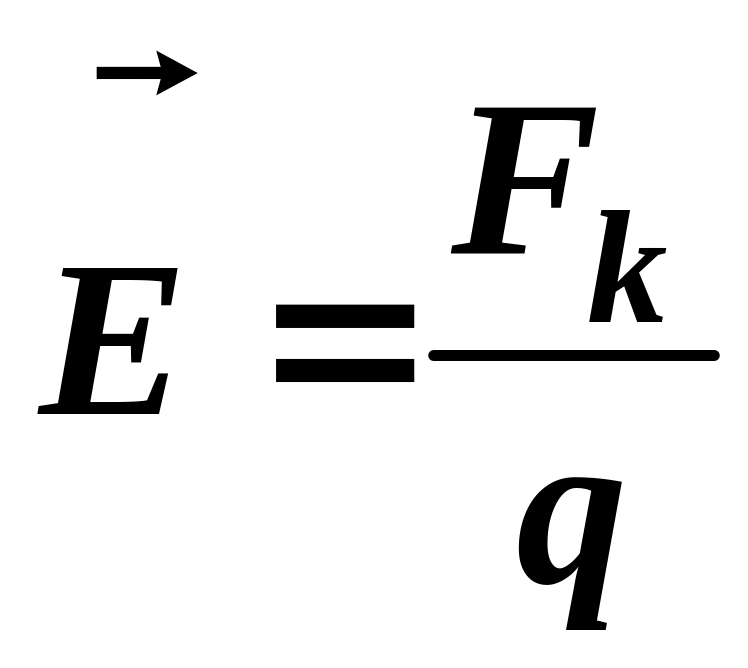где — сила, действующая со стороны электрического поля на заряд q.

[E] =Н/Кл = В/м,

Напряженность поля точечного заряда q на расстоянии r:

.

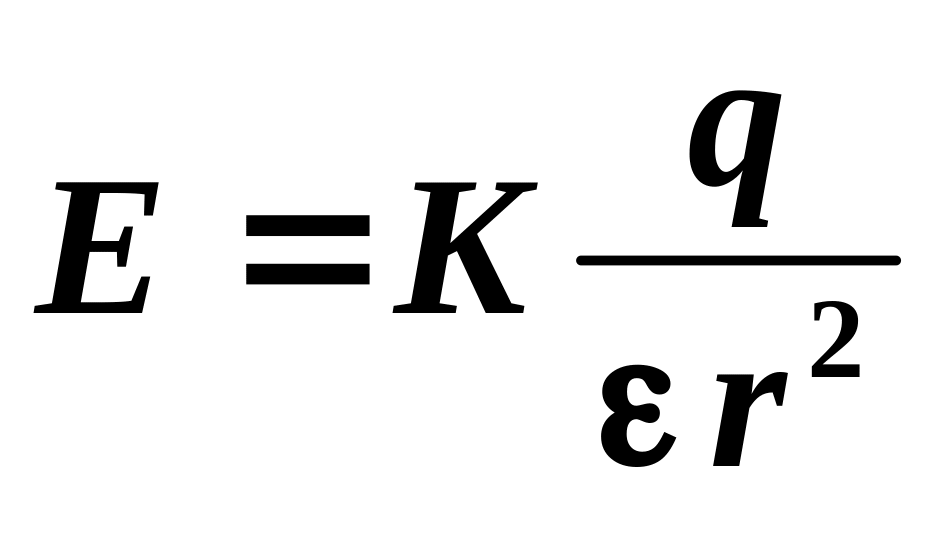Напряженность электрического поля, создаваемого бесконечной плоскостью с поверхностной плотностью заряда σ:

,

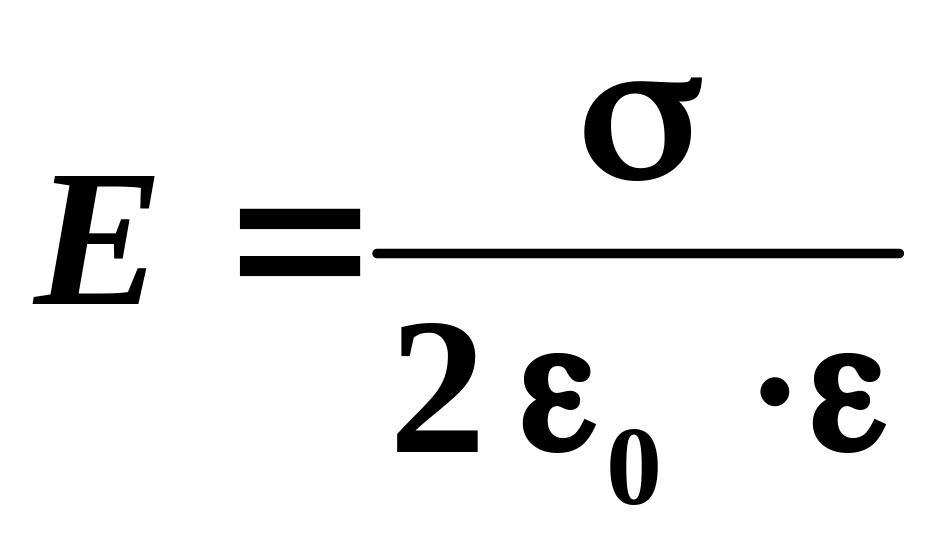где — элемент площади поверхности; [σ] = Кл/м².

Напряженность электрического поля, создаваемого плоским конденсатором с поверхностной плотностью заряда на обкладках σ:

.

Напряженность поля на расстоянии r от бесконечно длинной нити с линейной плотностью заряда :

,

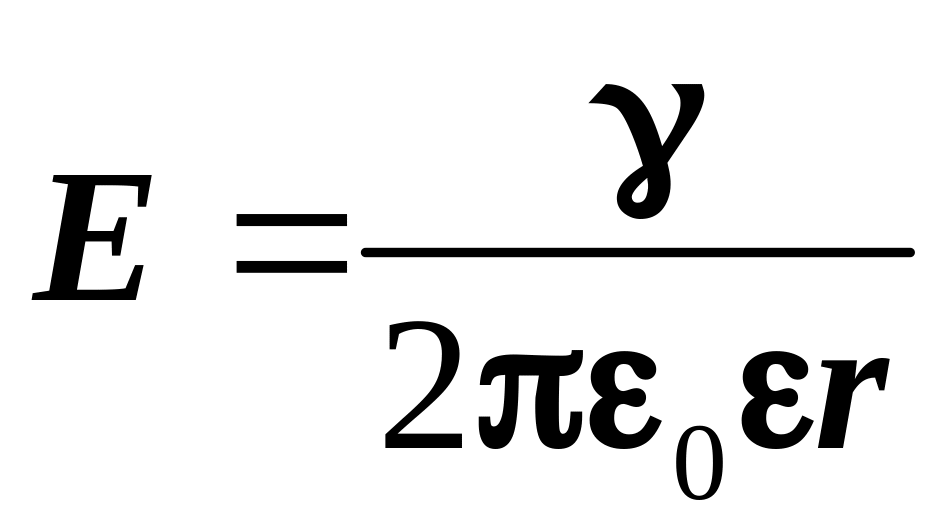где dl — элемент длины нити; [ ] = Кл/м.

Напряженность электрического поля, создаваемого n зарядами (принцип линейной суперпозиции для напряженности электрического поля):

Потенциальная энергия заряда q, находящегося в точке поля с потенциалом φ:

W = q φ₁ ;

[W] = Дж, [φ] = В.

Потенциал поля точечного заряда q на расстоянии r:

.

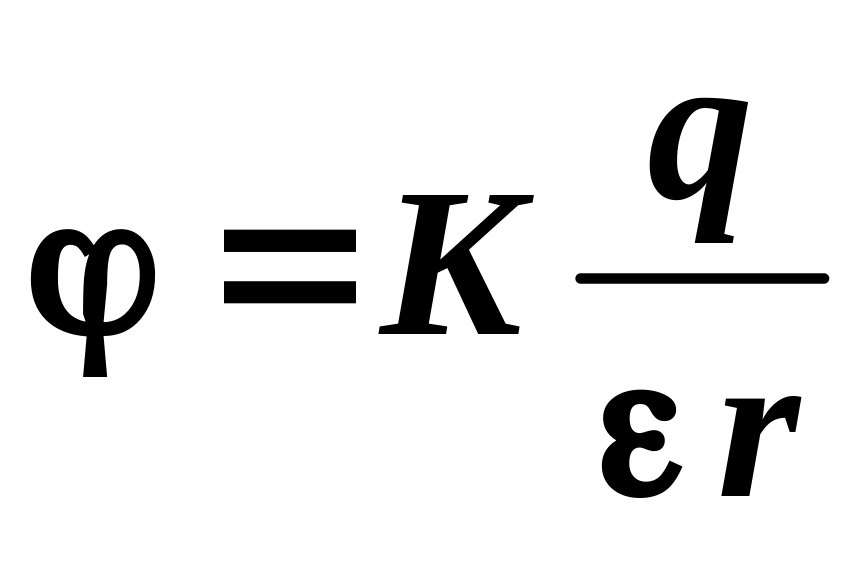Потенциал электрического поля, создаваемого n зарядами (принцип линейной суперпозиции для электрического потенциала):

φ = φ₁ + φ₂ +…+ φ_n.

Работа электростатического поля по перемещения заряда q, из точки с потенциалом φ₁ точку с потенциалом φ₂:

A = q (φ_{1 –} φ₂).

Связь напряженности и потенциала:

,

где dφ изменение потенциала вдоль силовой линии протяженностью dl.

Напряженность поля плоского конденсатора:

,

где U — разность потенциалов, d — расстояние между пластинами.

Электрическая емкость проводника:

,

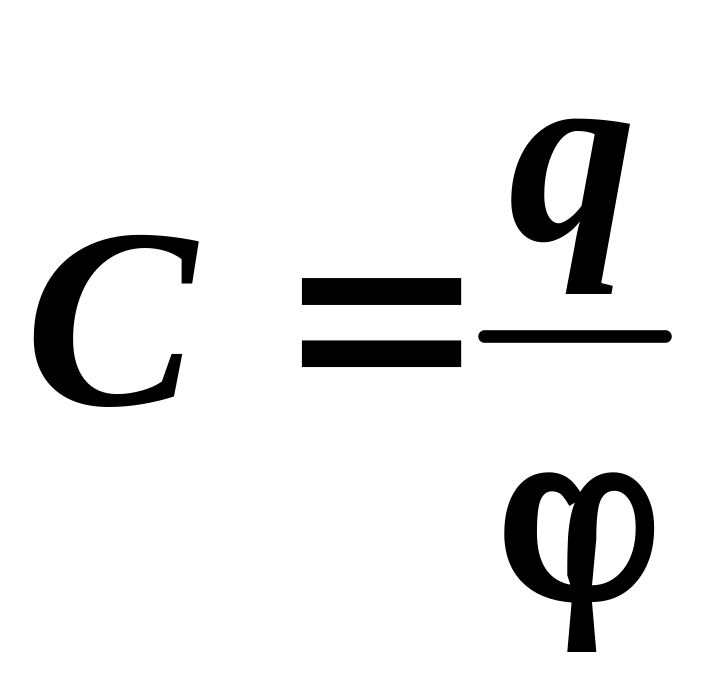где q — заряд, φ — потенциал проводника. [C] = Ф.

Электрическая емкость конденсатора:

,

где q — заряд, U — напряжение между пластинами.

Емкость плоского конденсатора:

.

S — площадь пластины, d — расстояние между пластинами.

Емкость проводящего шара:

,

где r — радиус шара.

Параллельное соединение конденсаторов:

Последовательное соединение конденсаторов:

.

Энергия заряженного конденсатора:

.

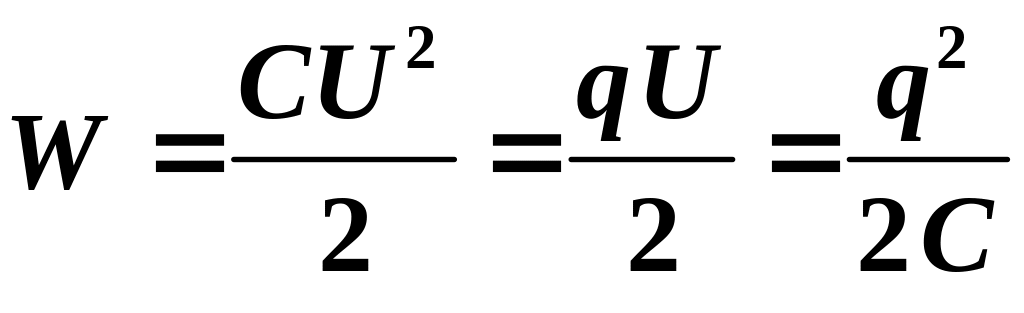Примеры решения задач

1. Закон Кулона.

Задача 1. Два одинаковых заряженных шарика, подвешенных на нитях одинаковой длины, опускают в керосин. Какова должна быть плотность материала шариков ρ, чтобы угол расхождения нитей в воздухе и в керосине был один и тот же? Плотность керосина 800 кг/м³, _ε =2.

Керосин

Рис.1 Рис.2

РЕШЕНИЕ

На каждый шарик с зарядом q в воздухе действуют три силы: сила тя­жести mg, сила натяжения нити Т и сила кулоновского отталкивания F_ko . Поскольку шарики находятся в равновесии, то результирующая всех сил равна нулю. Следовательно, сила электростатического отталкивания урав­новешивается силой F (см. рис.1),

F_ko = F = mgtgα (1)

В керосине, кроме указанных сил, на шарики действует выталкивающая си­ла Архимеда F_A. В этом случае сила кулоновского отталкивания F_K1 урав­новешивается силой F₁(см. Рис.2).

F_k1 = F₁ = (mg - F_A) tgα (2)

Сила Архимеда: F_a = ρ_kVg, где ρ_k - плотность керосина, V - объем ша­рика. Учитывая, что V = m/ρ, получаем:

.

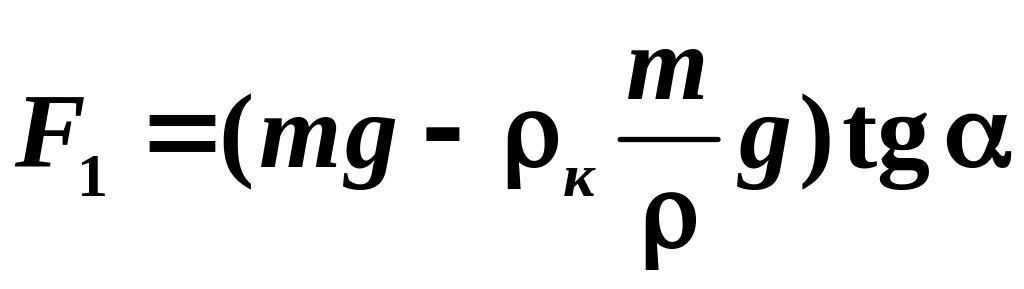Тогда выражение (2) принимает вид:

F_k1 = F₁ = (mg - ρ_k g) tgα (3)

Диэлектрическая проницаемость показывает, во сколько раз сила взаимо­действия зарядов в воздухе F_ko больше силы взаимодействия этих зарядов в среде: F_k0/F_k1.

С учетом соотношений (1) и (3), получаем:

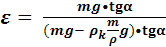или .

Отсюда следует, что плотность шариков: 

Вычисления: кг/ м ³.

Задача 2. В атоме водорода электрон вращается вокруг протона с угло­вой скоростью 10¹⁶ рад/с. Найти радиус орбиты электрона.

Рис.3

РЕШЕНИЕ

Со стороны протона р на электрон е действует сила кулоновского притяжения F_k, которая явля­ется центростремительной силой т.е. F_k =F_ц (см. рис.3).

По закону Кулона: ,

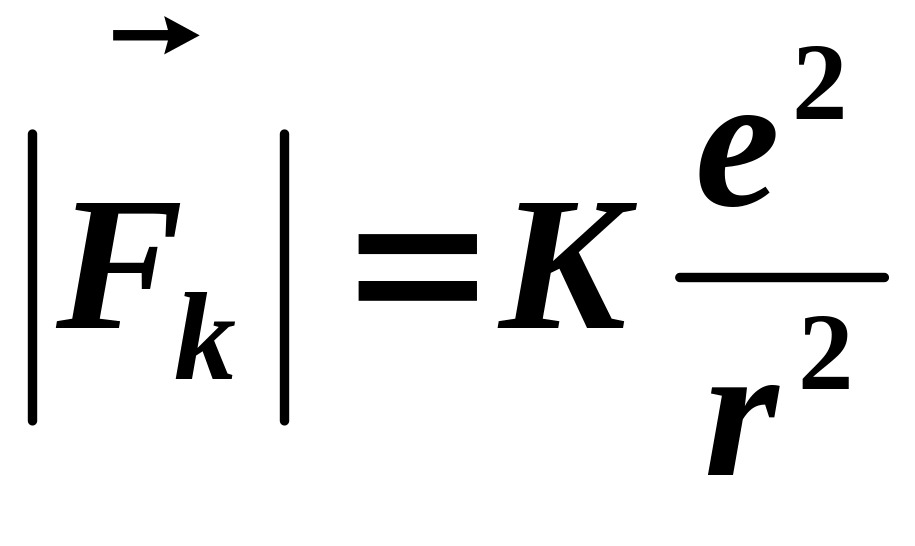где e = 1,6 10^-19 Кл — элементарный заряд (заряд протона +е, электрона -е).

По второму закону Ньютона:

Таким образом: =

Отсюда находим радиус орбиты: 

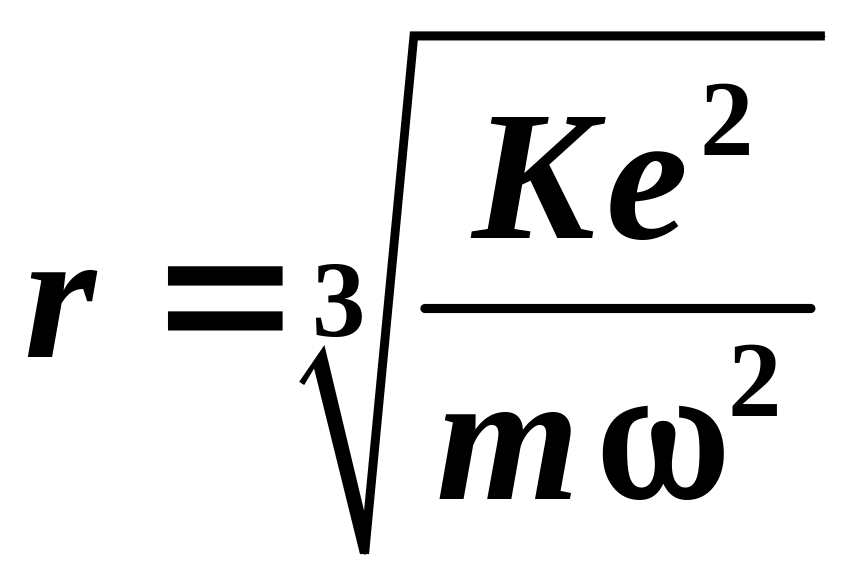
Проверка размерности:

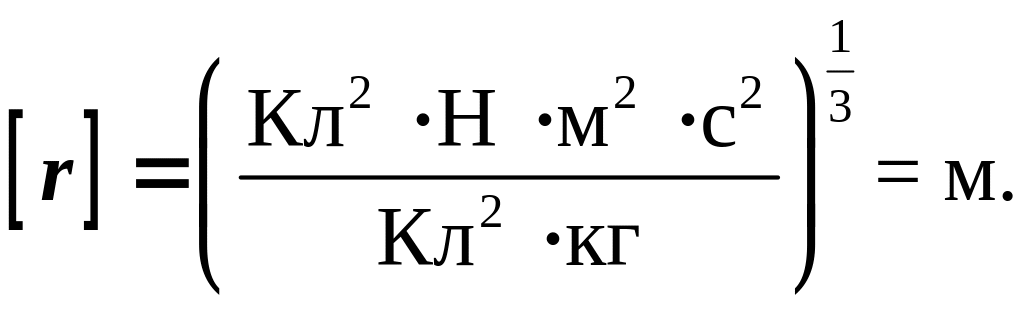
Вычисления: масса электрона m = 9,1∙ 10^-31 кг;

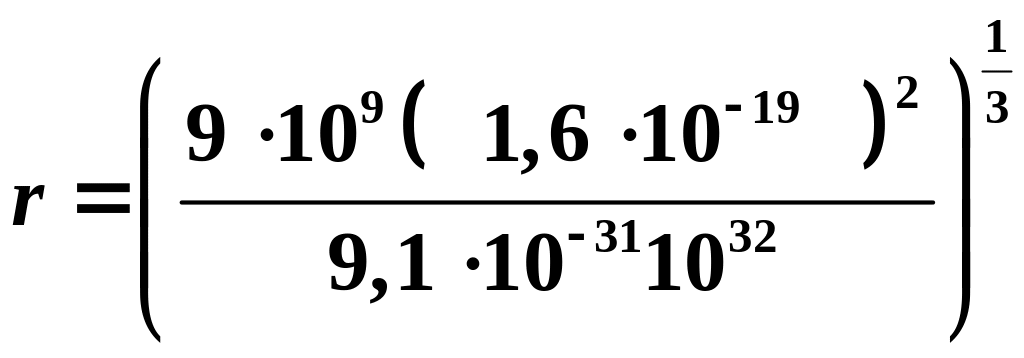= 1,4^.10^-10 м .