Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Донской государственный технический университет

Кафедра «ФИЗИКА»

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ.

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Методические указания к самостоятельным практическим занятиям

по дисциплине «Физика»

для студентов 1-го курса ИЭМ

технических специальностей

всех форм обучения

Ростов-на-Дону

2013

Составители:

кандидат физико-математических наук, доцент кандидат физико-математических наук, доцент кандидат физико-математических наук, доцент

В.В. Шегай Н.В. Дорохова В.П. Сафронов

УДК 537.8

Механические колебания и волны. Молекулярная физика и термодинамика: Метод. указания к самостоятельным практическим занятиям по дисциплине «Физика» / ДГТУ ГОУ, Ростов н/Д, 2013. — 25 с.

Методические указания представляют собой практическое руководство к самостоятельному решению задач по первой части курса физики. Они включают краткие теоретические сведения, справочные данные и задачи по темам: механические колебания, упругие волны, молекулярно-кинетическая теория идеальных газов и основы термодинамики.

Предназначены для студентов 1-го курса технических специальностей всех форм обучения.

Рецензент

кандидат физико-математических наук, доцент

Б.Б. Конкин

Научный редактор

кандидат физико-математических наук, доцент

В. В. Шегай

Ó	Государственное образовательное учреждение высшего профессионального образования Донской государственный технический университет

Оглавление

1.	Краткие теоретические сведения	3
2.	Примеры решения задач	9
3.	Задачи для самостоятельного решения	16
4.	Варианты заданий для самостоятельной работы	24
5.	Справочные данные	25
6.	Литература	25

Краткие теоретические сведения

1. Механические колебания и волны.

1.1. Дифференциальное уравнение гармонических колебаний имеет вид:

.

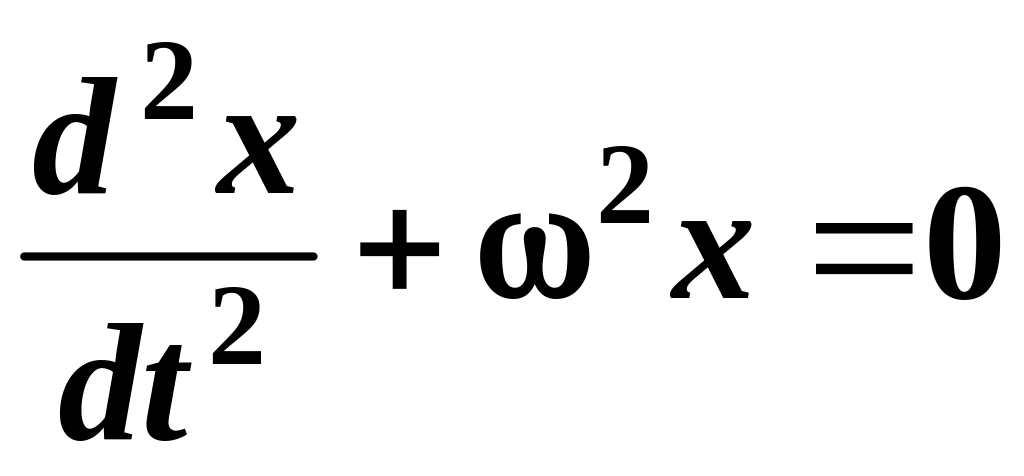Решением этого уравнения является закон гармонических колебаний:

.

где — отклонение колеблющейся величины от положения равновесия в момент времени t; — амплитуда колебаний; — фаза колебаний; — циклическая (круговая) частота; — период колебаний; — частота; — начальная фаза колебаний. и определяются из начальных условий.

1.2. Скорость точки, совершающей гармонические колебания:

,

где — амплитуда скорости.

1.3. Ускорение точки, совершающей гармонические колебания:

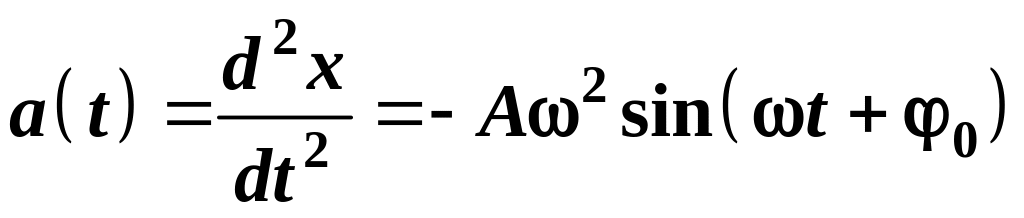
где — амплитуда ускорения.

1.4. Период и круговая частота свободных колебаний пружинного маятника:

, ,

где — масса груза; — жесткость (коэффициент упругости) пружины.

1.5. Период и круговая частота малых свободных колебаний физического маятника:

, ,

где — масса маятника; — момент инерции маятника относительно оси вращения; — расстояние от оси вращения до центра тяжести маятника; — ускорение свободного падения.

1.6. Период и круговая частота малых свободных колебаний математического маятника:

, ,

где — длина маятника.

1.7. Потенциальная энергия гармонических колебаний пружинного маятника:

.

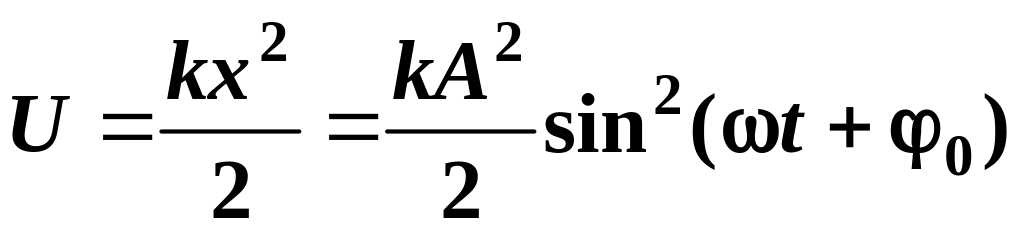1.8. Кинетическая энергия гармонических колебаний пружинного маятника:

.

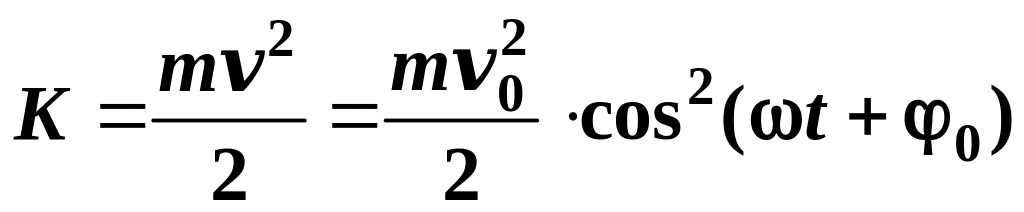1.9. Полная энергия гармонических колебаний пружинного маятника:

.

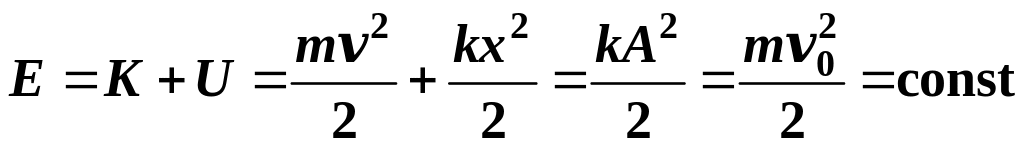1.10. Дифференциальное уравнение затухающих колебаний пружинного маятника:

,

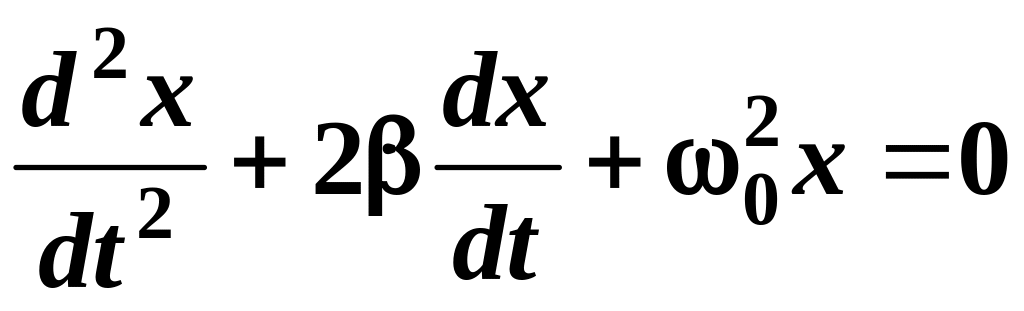где — коэффициент затухания; — коэффициент вязкого трения; 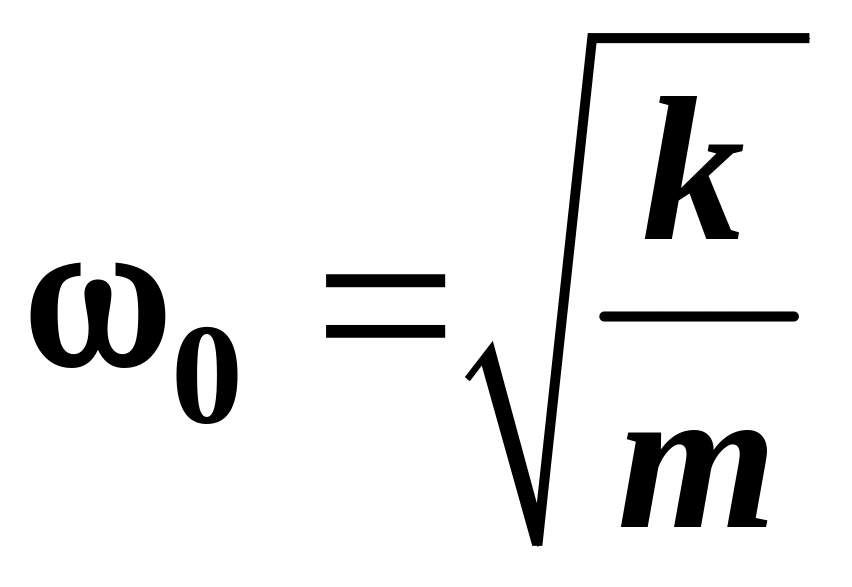— круговая частота свободных колебаний маятника.

1.11. Решением дифференциального уравнения затухающих колебаний является закон затухающих колебаний:

,

где — амплитуда затухающих колебаний; — круговая частота затухающих колебаний.

1.12. Логарифмический декремент затухания:

.

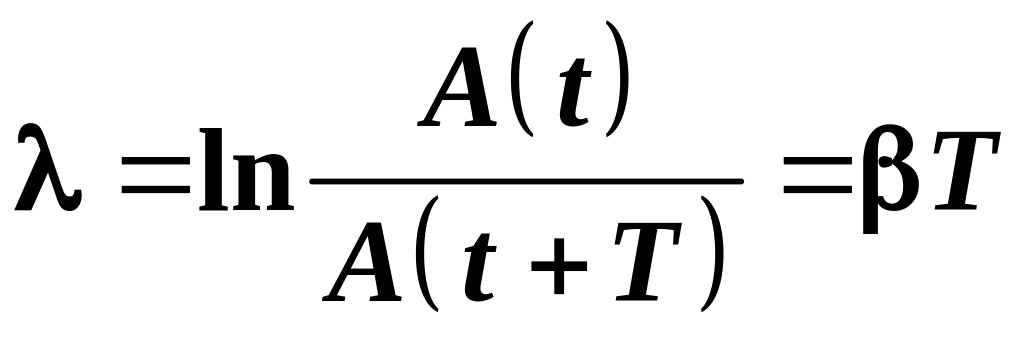1.13.Время релаксации:

.

1.14. Добротность:

.

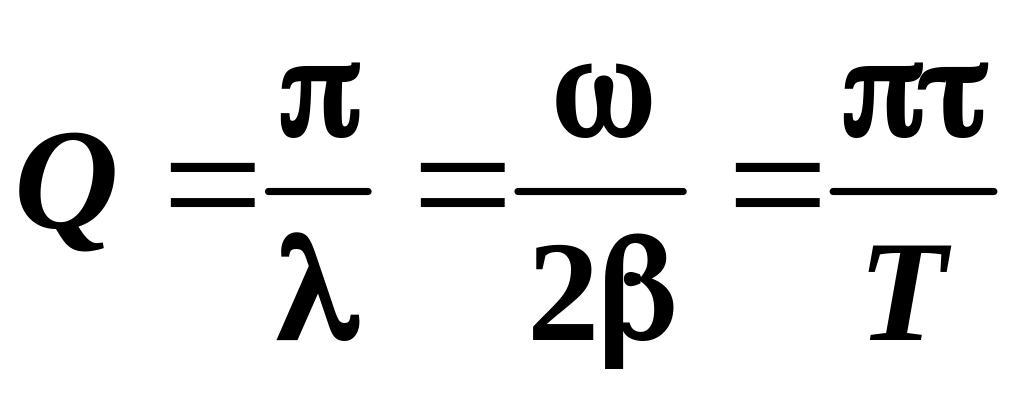1.15. Дифференциальное уравнение вынужденных колебаний:

,

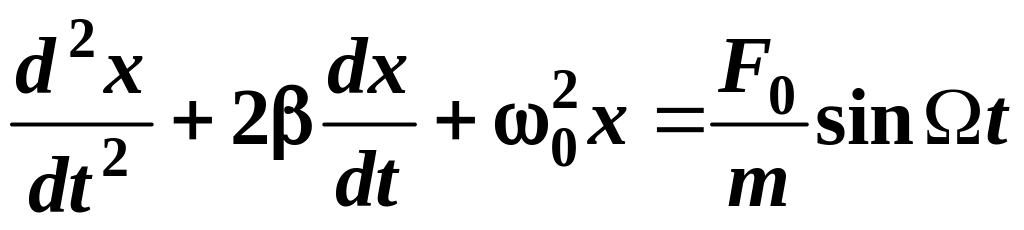где — циклическая частота вынуждающей силы, — максимальное значение (амплитуда) внешней силы.

1.16. Решение дифференциального уравнения для установившихся вынужденных колебаний:

,

где — амплитуда вынужденных колебаний; ; 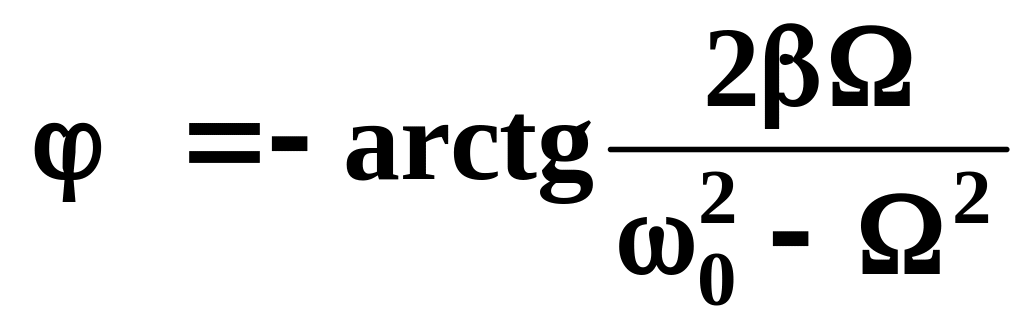— сдвиг фазы между смещением и внешней силой.

1.17. Условие механического резонанса:

,

и амплитуда резонансных колебаний:

.

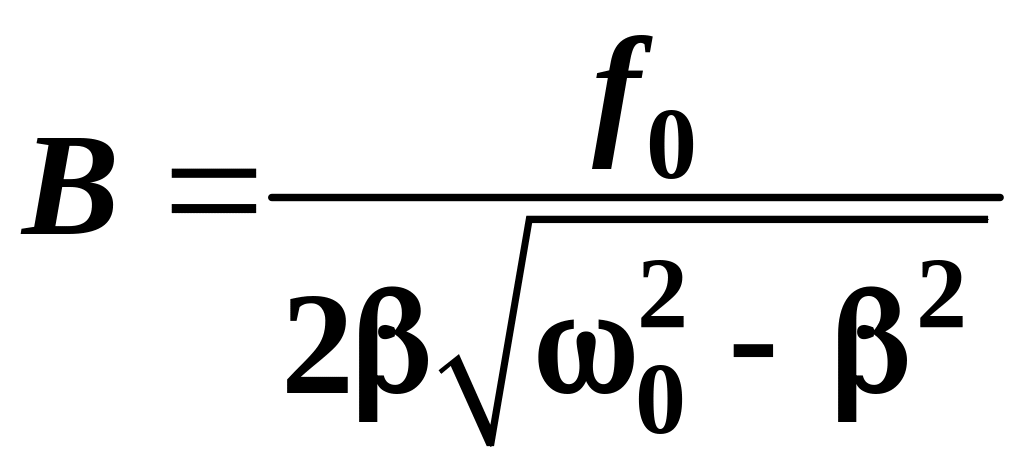1.18. Связь длины и скорости распространения волны:

.

1.19. Скорость распространения упругих продольных волн в тонких стержнях:

,

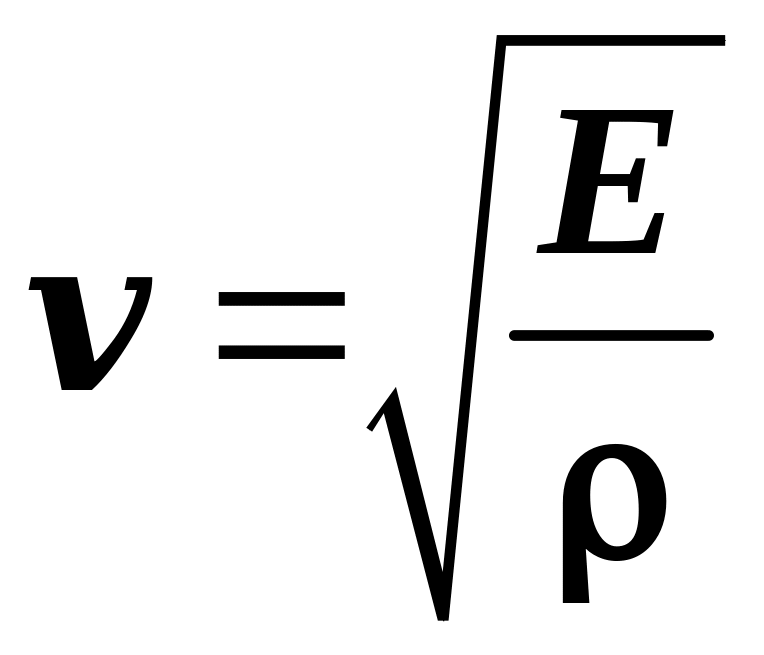где — модуль Юнга; — плотность материала стержня.

1.20 Скорость распространения упругих волн в газах:

,

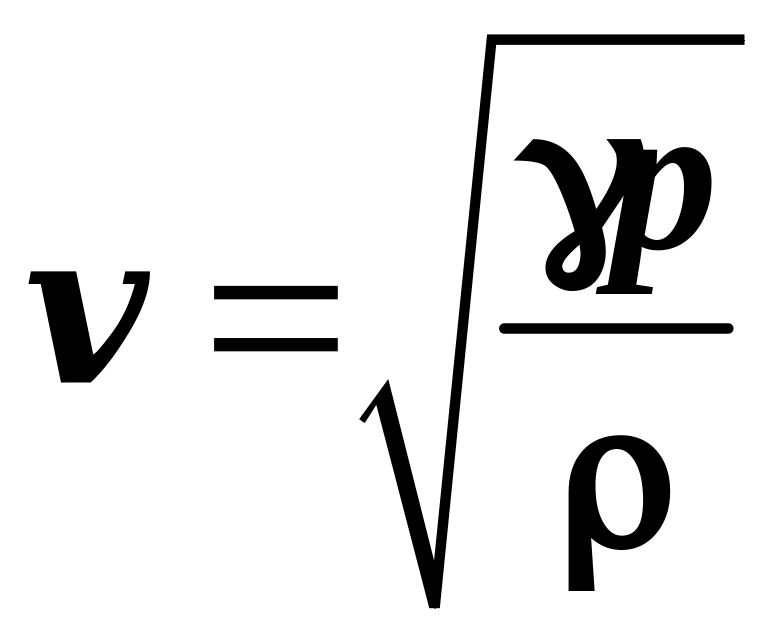где — показатель адиабаты; — давление; — плотность газа.

1.21. Уравнение плоской гармонической волны:

,

где — смещение частиц среды в точке в момент времени ; — волновое число; — амплитуда волны.

2. Молекулярная физика и термодинамика.

2.1 Молярная масса вещества:

,

где — масса одной молекулы; — постоянная Авогадро.

2.2. Количество вещества:

,

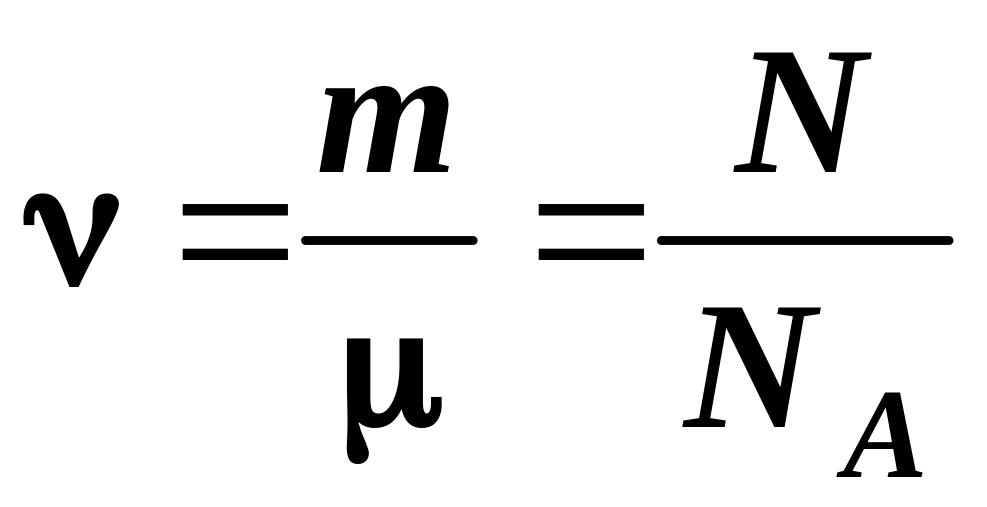где — масса вещества; — число молекул.

2.3. Уравнение состояния идеального газа (уравнение Менделеева ─ Клапейрона):

где — давление; — объем; — абсолютная температура газа; — универсальная газовая постоянная.

2.4. Связь между абсолютной температурой и температурой :

.

2.5. Связь между давлением и средней кинетической энергией поступательного движения молекулы идеального газа (основное уравнение молекулярно-кинетической теории идеальных газов):

,

где — концентрация молекул; 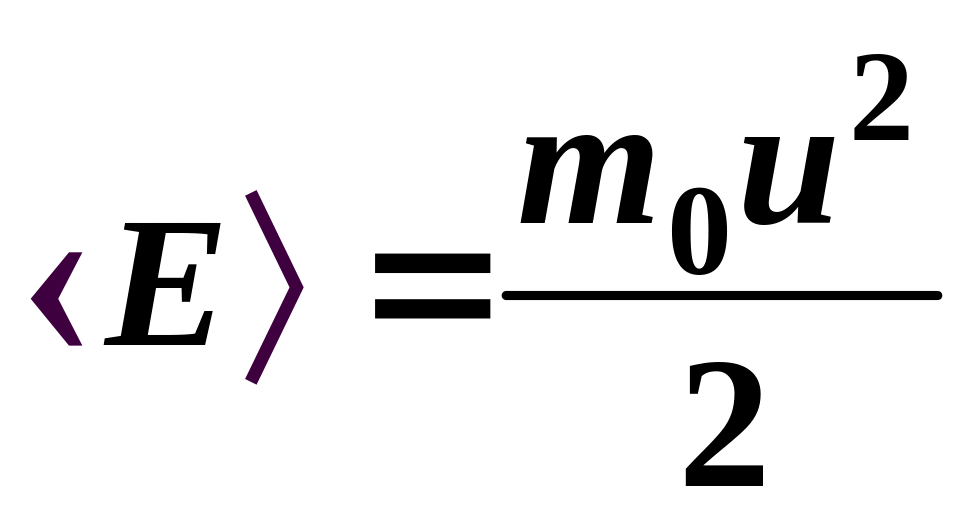, m₀ — молекулы, — средняя квадратичная скорость молекулы.

2.6. Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой:

,

где — постоянная Больцмана.

2.7. Связь между давлением, концентрацией и абсолютной температурой идеального газа:

.

2.8. Закон Максвелла распределения молекул идеального газа по скоростям определяет число молекул из общего числа молекул , которые обладают при данной температуре скоростями в интервале от до :

.

2.9. Скорости молекул идеального газа.

2.9.1. Наиболее вероятная скорость

.

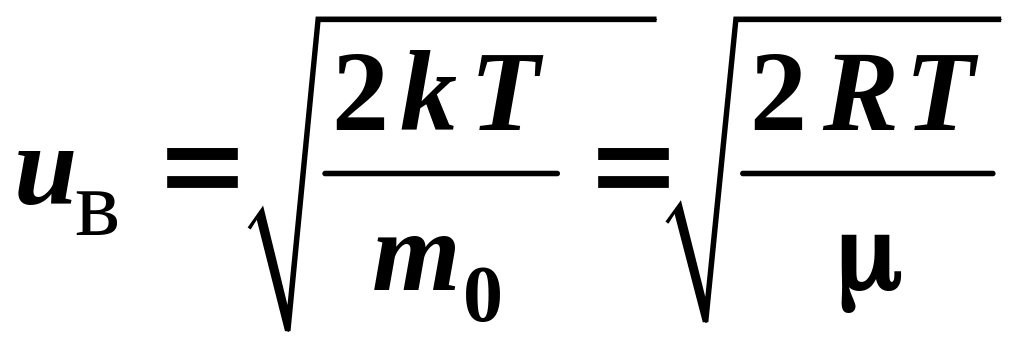2.9.2. Средняя квадратичная скорость

.

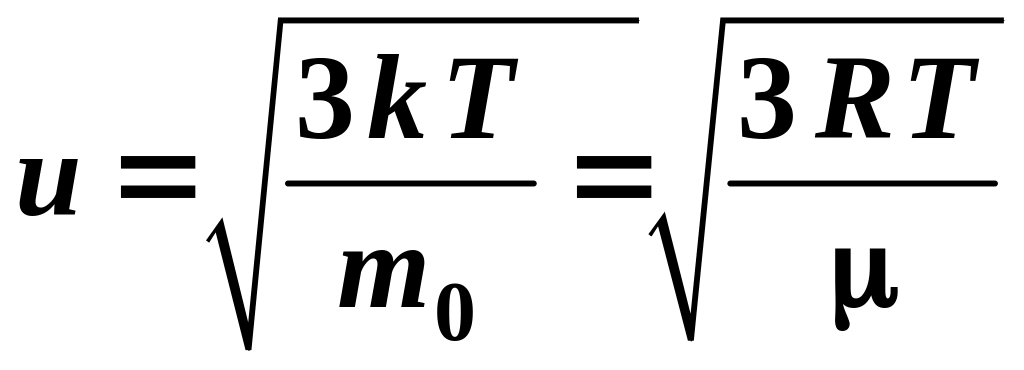2.9.3. Средняя арифметическая скорость

.

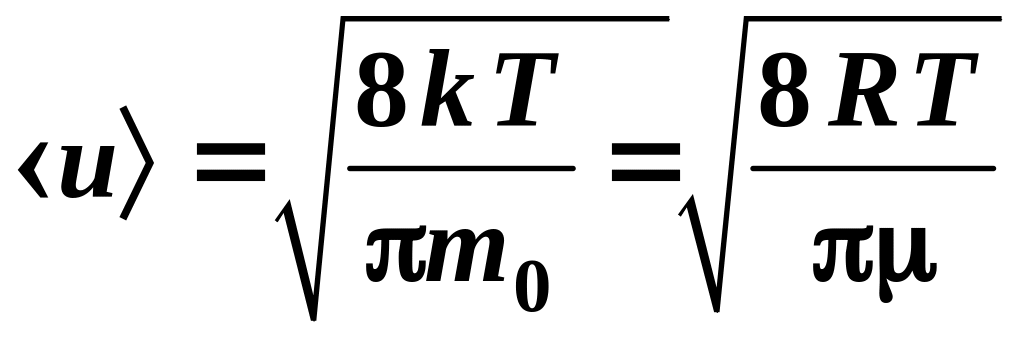2.10. Внутренняя энергия идеального газа:

,

где — число степеней свободы молекулы.

2.11. Первый закон термодинамики:

Количество теплоты , сообщенное системе, идет на приращение ее внутренней энергии и на совершение системой работы против внешних сил:

.

2.12. Работа при изменении объема газа от до :

.

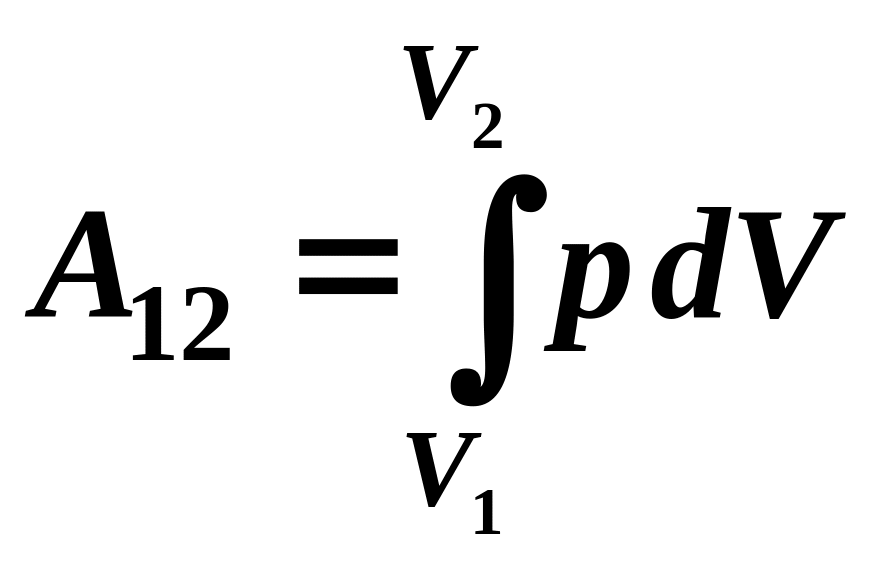2.13. Количество теплоты , необходимое для нагревания массы вещества:

,

где — удельная теплоемкость вещества, — изменение температуры.

2.14. Связь между молярной и удельной c_уд. теплоемкостями:

.

2.15. Изопроцессы в идеальных газах:

2.15.1. Изотермический процесс ( ):

Уравнение процесса (закон Бойля ─ Мариотта): .

Работа: .

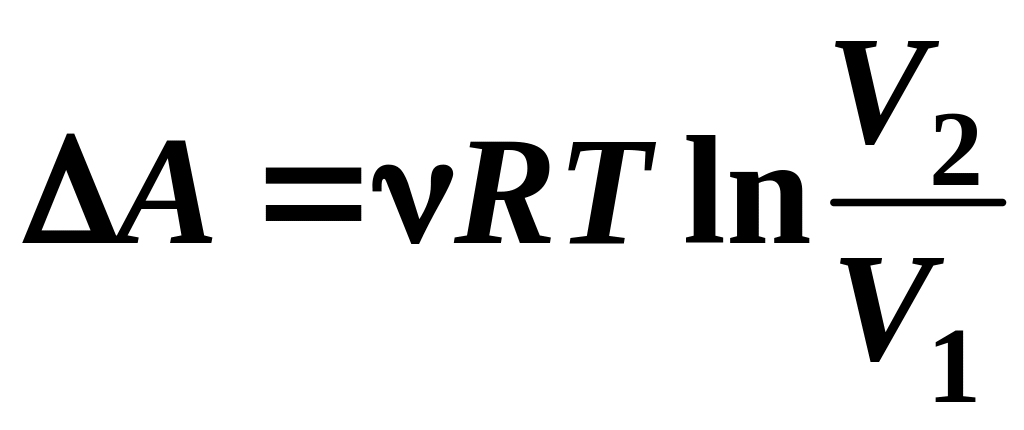Изменение внутренней энергии: .

Первый закон термодинамики: .

2.15.2. Изохорный процесс ( ).

Уравнение процесса (закон Шарля): .

Работа: A=0.

Изменение внутренней энергии: .

Молярная теплоемкость: .

Первый закон термодинамики: .

2.15.3. Изобарный процесс ( ).

Уравнение процесса (закон Гей-Люссака): .

Работа: .

Изменение внутренней энергии: .

Молярная теплоемкость: .

Первый закон термодинамики:

2.15.4. Адиабатный процесс ( ).

Уравнение процесса (уравнение Пуассона): ,

где — показатель адиабаты (коэффициент Пуассона).

Работа: .

Изменение внутренней энергии: .

Первый закон термодинамики: .

2.16. КПД теплового двигателя :

_,

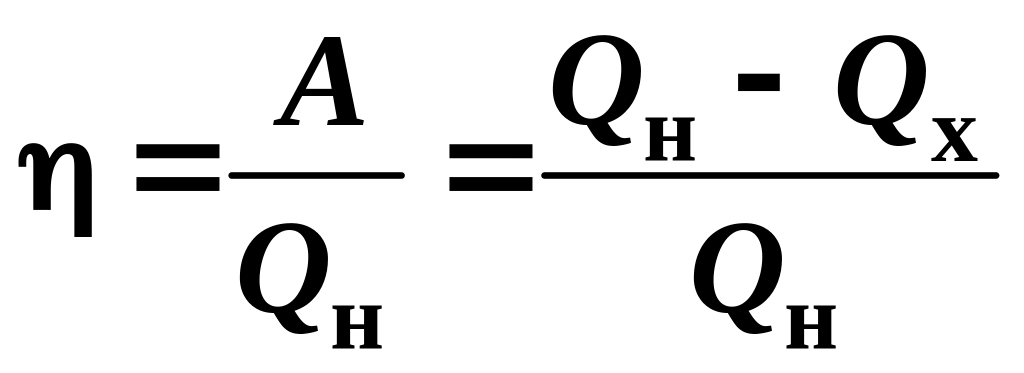где — теплота, полученная двигателем от нагревателя; — теплота, отданная двигателем холодильнику; — работа двигателя.

2.17. Максимальный КПД теплового двигателя (теорема Карно):

_,

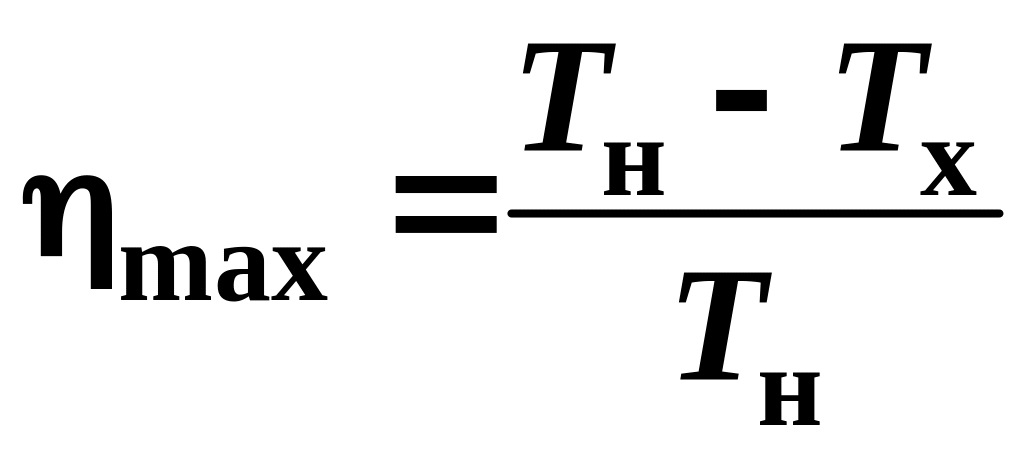где — температура нагревателя; — температура холодильника.