П рактические занятия №2 Проецирование точки

Модель проецирования точки Комплексный чертеж точки

А (15,24,20)

Определитель точки пространства - координаты х, у, z точки, т.е. расстояния точки от трех координатных плоскостей. Принимается, что плоскости проекций совмещены с координатными.

Условная запись определителя точки: А ( х , у , z , )

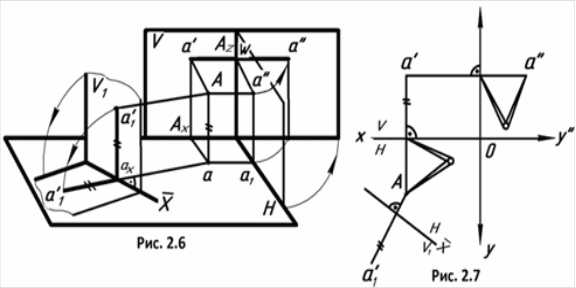
Проекцией точки называется точка пересечения проецирующего луча с плоскостью проекций (рис. 2.1).

Плоский чертеж получается совмещением одной из плоскостей проекций с другой плоскостью проекций вращением вокруг оси проекций.

Комплексным чертежом называется плоский чертеж, состоящий из проекций изображаемого образа, размещенных в проекционной связи друг с другом. Линия проекционной связи всегда перпендикулярна оси проекций, разделяющей данные изображения (рис. 2.2).

Чтение комплексного чертежа объекта проецирования

Результатом чтения комплексного чертежа является нахождение графического определителя изображаемого образа и его метрических и позиционных характеристик.

Для точки:

1. Определителем точки на чертеже является совокупность двух проекций точки: а: а´ а(х,у) – а´(х,z).

2. Координаты точки устанавливаются измерениями (см.рис.2.2).

Чтение чертежей точек, лежащих в плоскостях проекций и на оси Х

В(15,0,10); B€ V С(20,5,0); С € Н D(25,0,0); D € x

Рис. 2.3 Рис. 2.4 Рис. 2.5

Модель проецирования точки Комплексный чертеж

Точки на дополнительные плоскости

Проецирование прямой

Определитель прямой: две точки. Условная запись L(А,В). На чертеже прямую определяют двумя проекциями прямой.

L( аb, a΄ b´) или L(1_1,1΄)

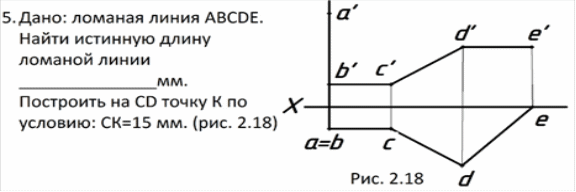
Точки на заданной прямой. Условие принадлежности

Точка принадлежит прямой, если проекция точки принадлежит одноименным проекциям прямой (см. точку С на прямой АВ - рис. 2.8 и 2.9).

Чтение чертежей прямых частного и общего положений

У пражнения

1.Построить чертежи точек

А(30.25.5)

L(10.0.30)

и проекции прямой, проходящей через эти точки.

Запишите, какое положение занимает эта прямая в пространстве (рис.2.14).

Рис. 2.14

2 . Построить недостающие проекции видимых точек В, С и Д, принадлежащих ребрам призмы. Записать координаты точек в указанной системе координат (рис. 2.15).